解析'三门问题'：Python在哲学中的角色

作者 | 小詹

责编 | 郭芮

本文我们用Python分析著名的“三门问题”。

不过在这之前 ，可以先来说点类似的。假如三个盒子里各有一个球，一次选择机会摸奖。你摸到了球，就奖励你一个脱发再续膏，解决程序员秃头烦恼。如果没摸到？那你就秃头吧......

Python实现之基本操作：

for i in range(time): box = [0,0,0] my_choice = random.randint(1,3) box[random.randint(1,3) - 1] = 1 if (i)%30==0: print("\n") if box[my_choice - 1]: count = count + 1 print("⬜",end=" ") else: print("⬛",end=" ")print("\n",count*100/time,"%")

概率是三分之一，这个没得跑，继续往下看。

三门摸奖之死门

三个盒子里有一个球，一次选择机会摸奖。这次可以加点料，当你第一次选择之后，上帝准确告诉你剩余两个选择中有一个是错的，空盒子，现在你剩下了自己原来的选择，和上帝没告诉你的那个选择。

现在给你一个选择，换不换：

• 坚持第一眼确认过眼神的盒子；
• 换成两个盒子里上帝没告诉你的盒子。

上帝真好，为了给程序员发福利排除一个错误选项，二分之一概率很 OK，就那个确认过眼神的盒子吧。

Python实现之坚持我的选择：

def God_hand(box,my_choice): all = 6 god_choice = random.randint(1,3)-1 while god_choice == my_choice: god_choice = random.randint(1,3)-1  if(box[god_choice]): return all - god_choice - my_choice return god_choiceGod_choice = God_hand(box,my_choice)my_choice = my_choice

嗯？？？不还是三分之一嘛，这有啥？等等，好像有点不对的地方。

三门摸奖之生门

这次我想选上帝没告诉我的那个盒子，我觉得我好像发现了什么。

Python实现之选择那个上帝没告诉我的盒子：

God_choice = God_hand(box,my_choice)my_choice = 6 - my_choice - God_choice

没错三分之二，概率变了，变了，变了！这里面的原因有很多，可以喊 6。不过还是继续往下看，我慢慢解释。

三门摸奖之无门

三个盒子里有一个球，一次选择机会摸奖，现在我已经不想生发了，我就想知道怎么操纵概率，头发只是小事。

这次来加点猛料，当你第一次选择之后，上帝随便开一个盒子，如果上帝开出了球，游戏结束，没有开出来，就到你的回合了。

还是给你一个选择，换不换？——换啊，肯定换，继续有上帝之手帮我操作概率，这天下我唾手可得。

Python实现之上帝之手：

def God_hand(box,my_choice): all = 6 god_choice = random.randint(1,3) while god_choice == my_choice: god_choice = random.randint(1,3) return god_choice

选上帝剩下的不行是吗 ，那我回来坚持我自己的......

Python实现之我的回合：

my_choice = my_choice

——你在逗我？这个上帝偷概率的。

好了，上面只是举个例子，下面我们来正经分析下三门问题的原型。

三门问题（Monty Hall problem）亦称为蒙提霍尔问题 、蒙特霍问题或蒙提霍尔悖论 ，大致出自美国的电视游戏节目 Let's Make a Deal 。

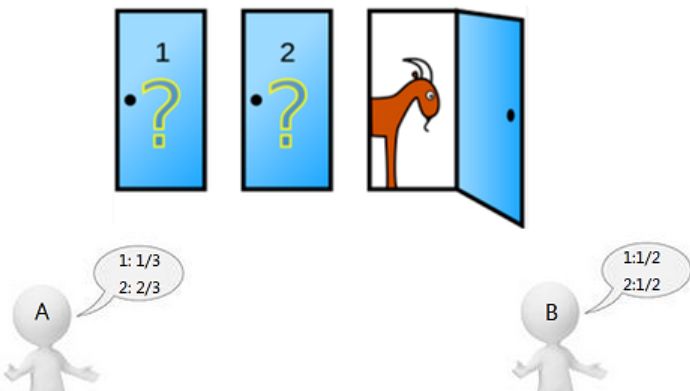
问题名字来自该节目的主持人蒙提·霍尔（Monty Hall）。参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门可赢得该汽车，另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门、但未去开启它的时候，节目主持人开启剩下两扇门的其中一扇，露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。

问题是：换另一扇门会否增加参赛者赢得汽车的机率？如果严格按照上述的条件，即主持人清楚地知道自己打开的那扇门后是羊，那么答案是会。不换门的话，赢得汽车的几率是1/3。换门的话，赢得汽车的几率是 2/3。

这个问题亦被叫做蒙提霍尔悖论：虽然该问题的答案在逻辑上并不自相矛盾，但十分违反直觉。这问题曾引起一阵热烈的讨论。

一般会用到的思路包括：横向的类比理解、纯数理计算、排列可能性。我的想法是，问题原型是三门问题，确实反直觉、反简单逻辑。于是我前后各自补充了两个实例，共三个渐进的问题：

1. 摸奖；
2. 摸奖+上帝之手排除+可选；
3. 摸奖+伪上帝之手开奖+伪可选 。

1、2 对比

1 三个里面总有两个是空的，上帝告诉我我没选的东西有什么用呢，我的选择不变，我的概率不变，依旧是三分之一。

1+1 先来两次 1，第一次我能选三个中的一个，过了几秒钟什么事情没发生，我可以换成别的，但我什么都不知道，怎么换还是三分之一。

2 第一次什么都不知道，但第二次选的时候我已经知道有一个排除项了，选那个非排除项、非首选项，选中几率扩大，而具体扩大的概率则需要定量数据分析，不是两个选择各自百分之五十，而是基于前两种情况下再做选择的概率分布。

更加重要的是，上帝是一个非随机的选择，上帝视角就决定了他对于随机概率的破坏。

对比结果

果然那个排除项不像想象中那么简单，拿到一个未知问题环境，应该坚持单一变量的原则，谨慎推导，增量修补，才能寻找到细微差异。

1、2、3 对比

探索从来不止于问题本身，为了更加深刻的探讨内涵，我增加第三项实验，如果这是个假上帝呢？他就和你一样，是一个选择者，他可能不是人，只是一个会产生结果，而它又从不会是你的选择。

于是，你回到了 1，相同的概率，你可能中途就知道自己选错了，也可能走到尽头才发现。你看似拥有选择，但你没有选择，你苦苦思索，希望做出更优的抉择，但是和一开始并无两样，你茫然依旧。

总结

这是一个简单复杂浅显深奥的概率问题，更不仅仅局限于数学。我可以在第二次让上帝之手放下无数空盒子打乱概率又发生变换，而概率在其中不同情况下的辗转变换，无一不彰显着一个永恒的真理：拥有选择权，才拥有概率。延伸一下，在更优的情况下，拥有选择权，才拥有更高的概率。

你知道勤奋占百分之九十九，但你不选这个盒子，任由上帝打开 。你知道兴趣多么助于你学习成长 ，但你不选这个盒子，任由其腐朽。你知道人工智能区块链量化交易的风口，但你不选这个盒子，任由别人打开。

我不愿你读过很多名人传记，发现过很多自己身上的影子，却懒惰愚昧的仰望着他们，把自己置于劣势的条件下做随机选择。

——谨以此文，与君共勉，走一条高概率成功的人生之路。

作者：小詹，一名双一流高校在读研究生 ，目前维护个人订阅号[小詹学Python]。主要涉及图像处理、网络爬虫、leetcode刷题和一些有趣的Python骚操作。

声明：本文为作者投稿，版权归其个人所有。