数组的基本知识

简介

数组（Array）是一种线性表数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据。

线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。其实除了数组，链表、队列、栈等也是线性表结构。而与它相对立的概念是非线性表，比如二叉树、堆、图等。之所以叫非线性，是因为，在非线性表中，数据之间并不是简单的前后关系。

常用操作

以下图数组为例：

读取

数组支持随机读取，随机读取的时间复杂度为 O(1)

查找

在数组（未排序）中查找指定的值就需要遍历数组，时间复杂度为 O(n)

插入

如图，往 k = 2 的位置插入 10。

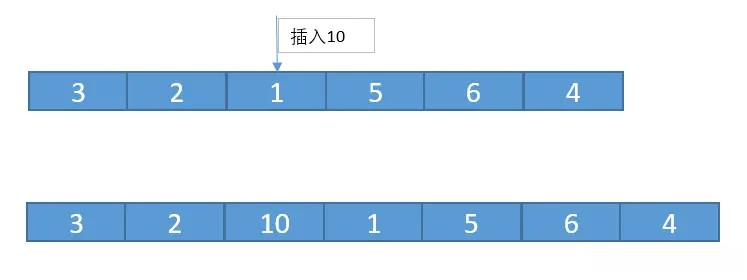
如果在数组的末尾插入元素，那就不需要移动数据了，这时的时间复杂度为O(1)。但如果在数组的开头插入元素，那所有的数据都需要依次往后移动一位，所以 最坏时间复杂度是O(n)。 因为我们在每个位置插入元素的概率是一样的，所以平均情况时间复杂度为(1+2+…n)/n=O(n)

删除

与插入类似，时间复杂度为 O(n)

与数组有关的常用算法

下面的算法题来自leetcode、牛客网上各个公司的面试题，以及《剑指Offer》上的例题。建议多刷题，刷题才是王道。

双指针(或双索引)

例1:leetcode的两数之和 II - 输入有序数组

给定一个已按照升序排列 的有序数组，找到两个数使得它们相加之和等于目标数。函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。说明:返回的下标值（index1 和 index2）不是从零开始的。你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。示例:输入: numbers = [2, 7, 11, 15], target = 9输出: [1,2]解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。

方法1：使用双向遍历，但是时间复杂度为O(n^2)

方法2：使用双指针，时间复杂度为O(n)

使用 start 指向开始位置， end 指向末尾位置。判断 nums[start] + nums[end] 的和与目标数 target 的关系。由于该数组为有序数组，当 nums[start] + nums[end] > target,则需要 end-- 才有可能 nums[start] + nums[end] == target；同理，当 nums[start] + nums[end] < target,则需要 start++

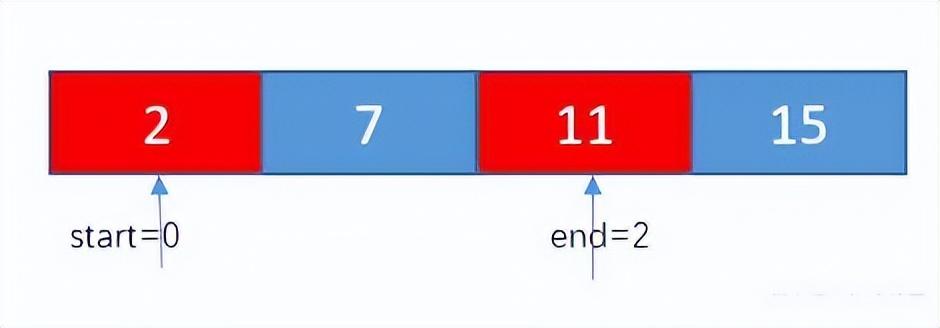
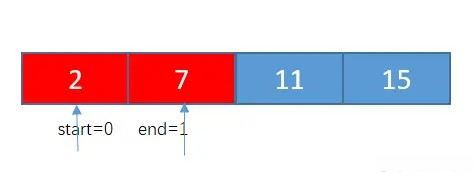
由于 nums[start] + nums[end] = 17 > target = 9,所以 end --，得到 end = 2

nums[start] + nums[end] = 13 > target = 9,所以 end --，得到 end = 1;最后计算 nums[0] + nums[1] == 9,即得到结果。

代码如下：

class Solution {    public int[] twoSum(int[] numbers, int target) {        if(numbers == null || numbers.length <= 1)return new int[2];//判断输入数组是否合法        int start = 0;        int end = numbers.length - 1;        while(start < end){            int sum = numbers[start]+numbers[end];            if(sum == target){                break;            }else if(sum > target){                end--;            }else{                start++;            }        }        int[] res = new int[2];        res[0] = start+1;        res[1] = end+1;        return res;    }}

例2：长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的连续子数组，返回 0。示例: 输入: s = 7, nums = [2,3,1,2,4,3]输出: 2解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。复制代码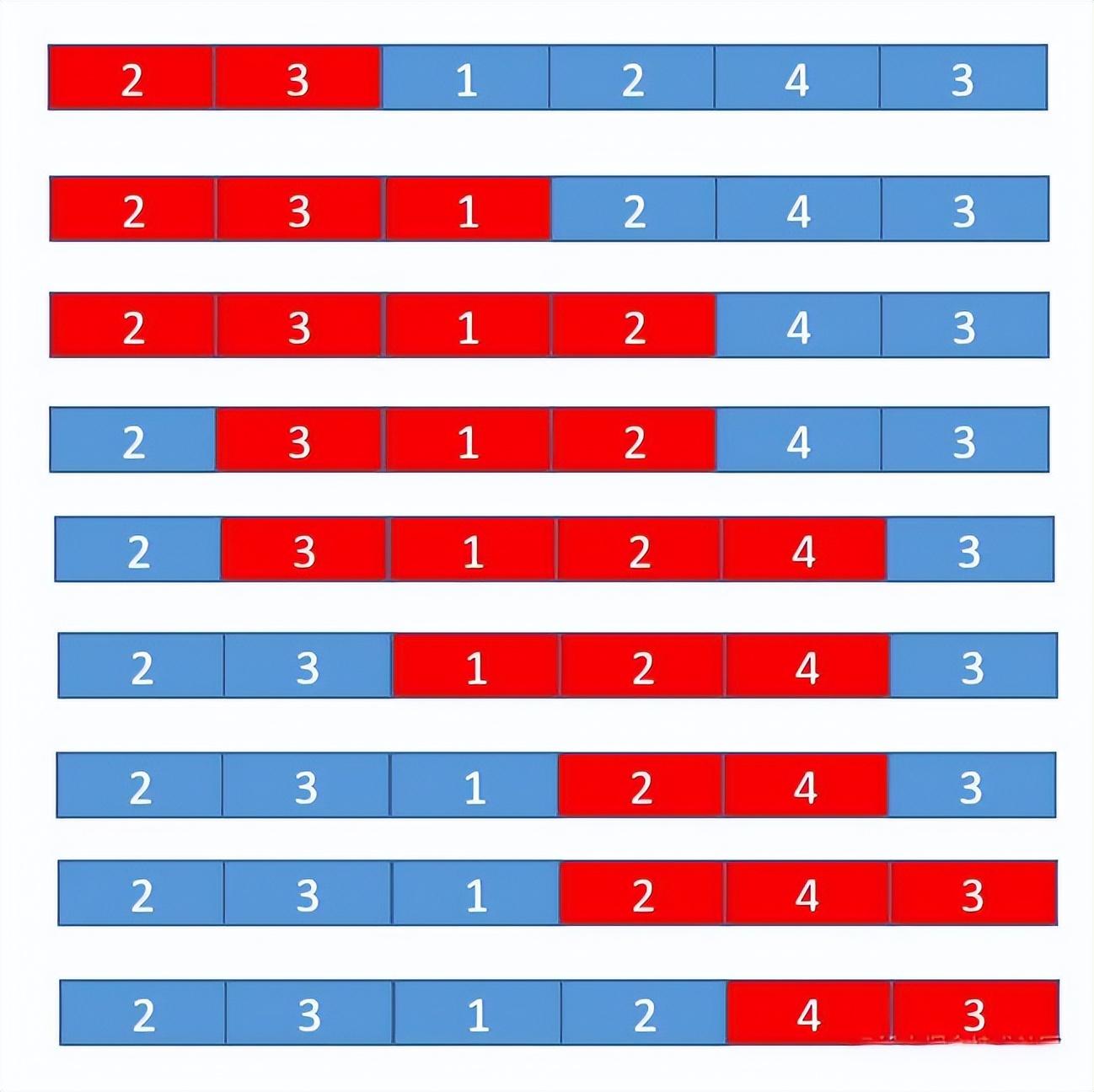

如图所示：

定义两个指针i,j分别指向0,1;其和 sum = 2 + 3 < s = 7,所以让 j++，直到其 sum >= s;如图第三个表格中，其和 sum = 8 > s = 7,此时记录 res = 4,并让 i++;如图所示，依此类推 就可以获得 res = 2.

代码如下

class Solution {    public int minSubArrayLen(int s, int[] nums) {        if(nums == null || nums.length <= 0)return 0;        int start = 0;        int end = 1;        int min = 1;        int sum = nums[0];        int res = Integer.MAX_VALUE;        while(true){           if(sum >= s){               res = Math.min(min,res);           }            if(sum > s){               sum -= nums[start];               min--;               start++;           }else{               if(end >= nums.length)break;               sum += nums[end];               end++;               min++;           }        }        if(res == Integer.MAX_VALUE)return 0;        return res;    }}

利用快速排序算法思想

示例：数组中的第K个最大元素（重要，面试常问）

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。示例 1:输入: [3,2,1,5,6,4] 和 k = 2输出: 5示例 2:输入: [3,2,3,1,2,4,5,5,6] 和 k = 4输出: 4说明:你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

解法1：先将数组排序，然后就可以通过 nums[nums.length - k] 获取我们所需要的元素.由于使用了排序算法，该算法的时间复杂度为 O(nlogn)

解法2：利用快速排序的原理，只需要 O(n) 的时间复杂度就可以获取第k大的元素,这也是一般面试需要我们懂的算法。

算法思路：随机在数组中找出一个数p，将数组中大于这个数p的元素放在右边，小于p的放在左边，如图

则p所在的位置 index = 4,即p = 4 为数组中第4小的数，反之，p = 4 即为数组中第三大的数。由于 p = 4 自己以及前面的数不可能是我们所需要找到的元素，所以截断 [0,3]的元素,从数组[4,5]范围内中重复开始的步骤找第k大的元素.

如图，p = 5 时为第二大的元素，即返回结果。

来自作者liweiwei1419的代码实现如下

public class Solution {    public int findKthLargest(int[] nums, int k) {        int len = nums.length;        int left = 0;        int right = len - 1;        // 转换一下，第 k 大元素的索引是 len - k        int target = len - k;        while (true) {            int index = partition(nums, left, right);            if (index == target) {                return nums[index];            } else if (index < target) {                left = index + 1;            } else {                right = index - 1;            }        }    }    /**     * 在数组 nums 的子区间 [left, right] 执行 partition 操作，返回 nums[left] 排序以后应该在的位置     * 在遍历过程中保持循环不变量的语义     * 1、[left + 1, j] < nums[left]     * 2、(j, i] >= nums[left]     *     * @param nums     * @param left     * @param right     * @return     */    public int partition(int[] nums, int left, int right) {        int pivot = nums[left];        int j = left;        for (int i = left + 1; i <= right; i++) {            if (nums[i] < pivot) {                // 小于 pivot 的元素都被交换到前面                j++;                swap(nums, j, i);            }        }        // 在之前遍历的过程中，满足 [left + 1, j] < pivot，并且 (j, i] >= pivot        swap(nums, j, left);        // 交换以后 [left, j - 1] < pivot, nums[j] = pivot, [j + 1, right] >= pivot        return j;    }    private void swap(int[] nums, int index1, int index2) {        int temp = nums[index1];        nums[index1] = nums[index2];        nums[index2] = temp;    }}

位运算知识

示例：

一个整型数组里除了一个数字之外，其他的数字都出现了两次。请写程序找出这个只出现一次的数字复制代码

预备知识：异或运算：如果a、b两个值不相同，则异或结果为1。如果a、b两个值相同，异或结果为0。

代码实现如下：

//num1,num2分别为长度为1的数组。传出参数//将num1[0],num2[0]设置为返回结果public class Solution {    public int FindNumsAppearOnce(int [] array) {        int sum = array[0];        for(int i = 1;i < array.length;i++){            sum ^= array[i];        }        return sum;    }}

空间换时间

通过增加空间复杂度来降低时间复杂度，这是常用的降低时间复杂度的思路。相关的算法题如下：

• 除自身以外数组的乘积
• 丑数

二维数组相关

• 利用二维数组记忆化的DFS的算法题:岛屿的最大面积
• 二维数组遍历:对角线遍历
• 二维数组旋转:旋转矩阵

必需掌握代码实现

• 实现一个支持动态扩容的数组
• 实现一个大小固定的有序数组，支持动态增删改操作
• 实现两个有序数组合并为一个有序数组

常问的算法题

• 求三数之和
• 求众数
• 求缺失的第一个正数
• 数组中只出现一次的数字
• 数组中的第K个最大元素
• 数组中出现次数超过一半的数字