树状数组，经典树形数据结构之一，代码很短，但其蕴含的算法思想却非常精妙。可以这么说，刷算法题却不懂树状数组，那绝对算是一大遗憾。

树状数组，常用于高效处理「一个数组的更新以及前缀和的求取」。具体来说，其常用于高效求解如下问题：

给定一个长度为 n 的数组 nums，需要支持两类操作：操作 1: 将 nums[i] 的数值增加 v操作 2: 求取 nums[1] + nums[2] + ... + nums[i] 的值

对于上述问题，如果我们采用直接的做法，则操作 1 的时间复杂度为 O(1)，操作 2 的时间复杂度为 O(n)。假如一共有 q 次操作，则总的时间复杂度为 O(qn)。

而如果使用树状数组来求解，则操作 1 和操作 2 的时间复杂度均为 O(log(n))。假如一共有 q 次操作，则总的时间复杂度为 O(qlog(n))。对比之前的做法，树状数组的解法在时间复杂度上有根本性的优势，而这也正是我们学习该算法的原因。

树状数组

树状数组加快运算的关键，在于对二进制的进一步挖掘，因此我们首先来回忆一下二进制。

以正整数 29 为例，其二进制为 11101，因此 29 可以根据其二进制进一步表示为：

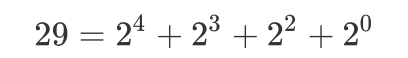
根据这一特点，我们可以重新思考之前的「操作 2」，即如何快速求取数组 [1, 29] 的和？

仿照之前对 29 的二进制拆分，我们也可以将 [1, 29] 拆分成如下四个区间的相加：

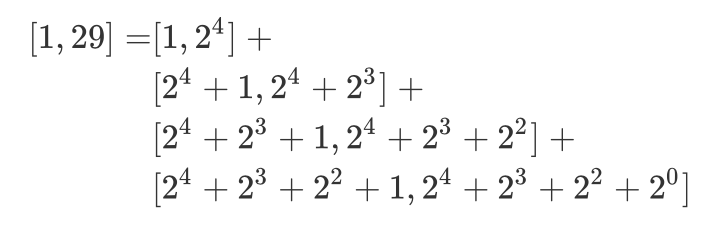
观察上述四个区间，可以发现四个区间的长度依次为 2^4、2^3、2^2、2^0。并且对于每一个区间来说，其区间长度恰好等于「区间右端点二进制中最低位的 1 对应的数值」。以区间 [2^4 + 1,2^4 +2^3] 为例，其区间长度为 2^3，而其区间右端点为 2^4 +2^3，二进制为 11000，其中最低位的 1 在第 3 位，对应的数值为 2^3，恰好等于其区间长度。

lowbit(x)

为了更好地形式化描述上述观察，我们引入 lowbit(x) 函数，表示「x 二进制中最低位的 1 对应的数值」。例如 29，其二进制为 11101，则最低位的 1 在第 0 位，对应的数值为 2^0，即 lowbit(29) = 1。再比如 16，其二进制为 10000，则最低位的 1 在第 4 位，对应的数值为 2^4，即 lowbit(16) = 16。

理解完 lowbit(x) 的功能后，我们给出其代码形式：

int lowbit(x) {    return x & (-x);}

代码非常短，但想要理解却需要一些原码、补码的知识。简单来说，在计算机中，所有整数都是用补码的形式来存储的，对于正整数 x 来说，其补码形式就是其二进制的形式。但对于负数 -x 来说，我们需要将 x 的二进制形式按位取反再加 1。

依旧以 29 和 16 为例，并且用 8 位二进制的形式来表示：

原理讲解

有了 lowbit(x) 函数，我们可以更容易地表示 [1, 29] 的拆分形式：

由此一来，我们可以更容易地发现四个区间的长度依次为 lowbit(16)、lowbit(24)、lowbit(28)、lowbit(29)，即 2^4、2^3、2^2、2^0。

到了这一步，我们便推导出了树状数组 c 的含义，即 c[x] 表示区间 [x - lowbit(x) + 1,x] 的和，即：

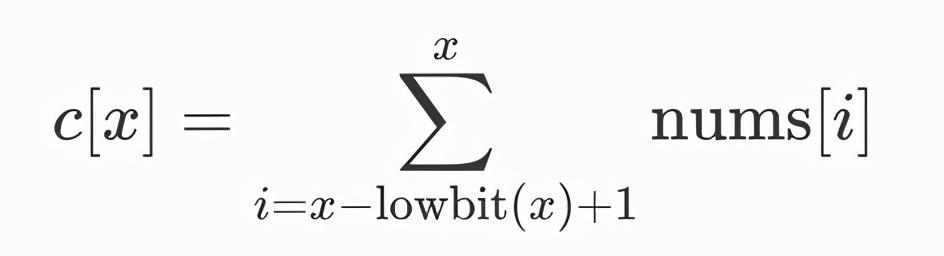
因此 [1, 29] 的和可以表示为：

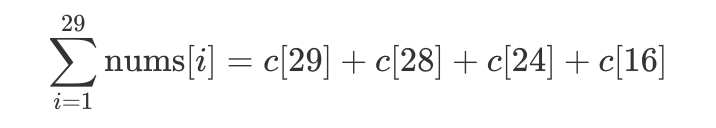
除此之外，我们还可以发现：

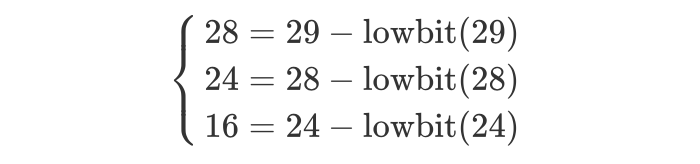
由此，我们可以得到树状数组关于操作 2，即求取 [1, x] 区间和的代码：

int query(int x) {    int res = 0;    // 当 i 等于 0 时，退出 for 循环    for (int i = x; i; i -= lowbit(i)) res += c[i];    return res;}

至此，还剩下一个函数未讲解。即对于操作 1 来说，当 nums[i] 的数值增加了 v，树状数组 c 该如何变化？

由于 c[x] 表示区间 [x - lowbit(x) + 1, x] 的和，因此我们只需要将所有覆盖了 nums[i] 的 c[x] 均加上 v 即可。由此问题转变为了「如何寻找到所有覆盖了 nums[i] 的 c[x]」？

寻找的方法非常简单，我们先直接给出代码：

void update(int x, int v) {    // n 为树状数组的长度    for (int i = x; i <= n; i += lowbit(i)) c[i] += v;}

观察上述代码，我们可以发现只需要令 i 不断加上 lowbit(i)，即可更新所有对应区间覆盖了 nums[i] 的 c[x]。

想要理解这个结论，我们需要先思考 i + lowbit(i) 究竟意味着什么？

我们假设 nums[i] = 109，查看 nums[i] 能否通过不断加 lowbit(i) 更新到 c[128]，即对应 [1, 128] 的区间。

109 的二进制为 01101101，其不断加 lowbit(i) 的结果如下：

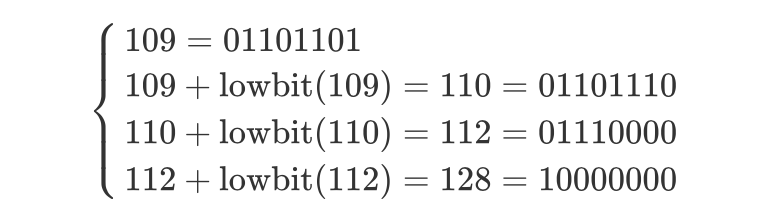
观察上述结果，最终的确更新到了 128。事实上，109 对应的二进制中，「最低位的 1 前面的 0」的位置分别是 1、4、7。在其不断加 lowbit(i) 的过程中，最低位的 1 不断向前挪到最近的一个 0，即 110、112、128 最低位的 1 分别为 1、4、7。

因此我们可以发现，不断加 lowbit(i) 的过程，即为将二进制中最低位的 1 不断向前挪到最近的一个 0 的过程。

回到前面的问题，「为何令 i 不断加上 lowbit(i)，即可更新所有对应区间覆盖了 nums[i] 的 c[x]」？

我们假设 c[x] 对应的区间 [x - lowbit(x) + 1, x] 覆盖了 nums[i]，且 c[x] 最低位 1 的位置为 pos。则 nums[i] 的二进制形式在 [0, pos] 位中必定存在 1。

此时分两种情况，若 nums[i] 二进制的 pos 位为 1，则 nums[i] = x；若 nums[i] 二进制的 pos 位不为 1，则 nums[i] 在不断加 lowbit(i) 的过程中，最低位的 1 一定会挪到 pos 位，即在加 lowbit(i) 的过程中达到 x，由此可以证明之前的结论。

树形结构

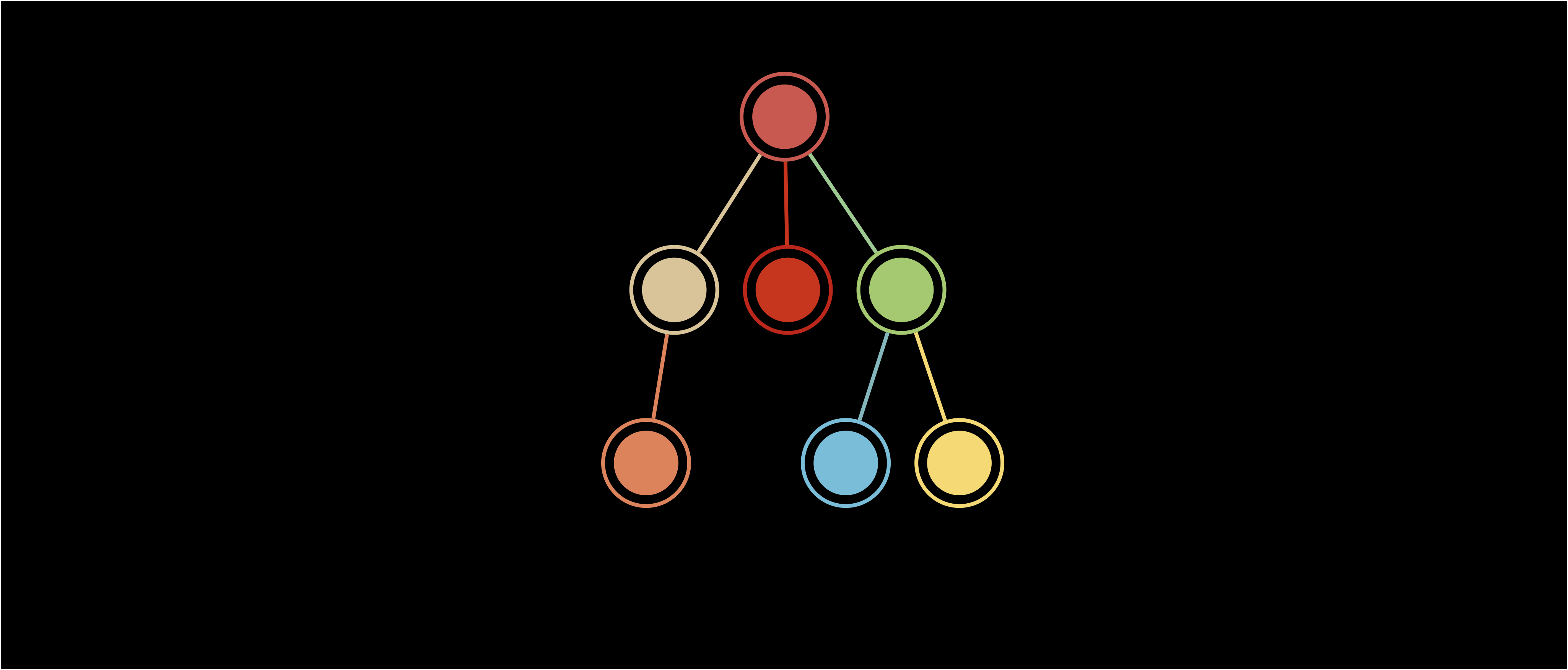
讲解完树状数组的原理后，我们再给出树状数组的树形图，来帮助大家进一步理解该数据结构。

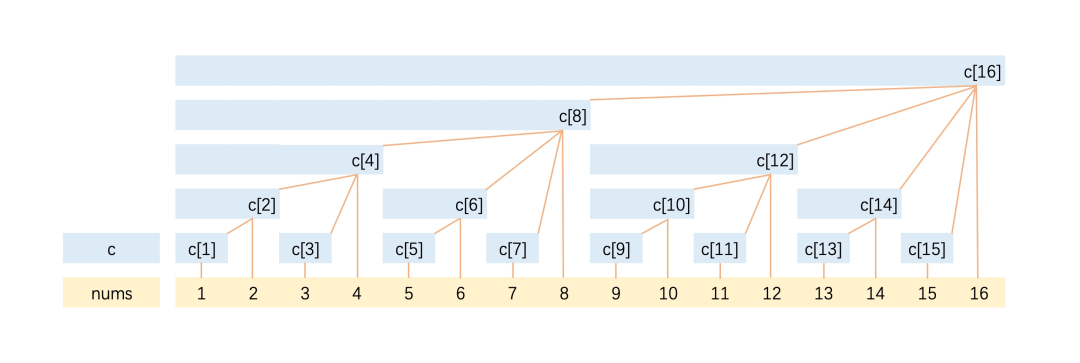
上图最下边一行为 nums 数组，代表 n 个叶节点，其上方为树状数组 c，满足以下 5 条性质：

1. 每个内部节点 c[x] 保存以它为根的子树中所有叶节点的和
2. 每个内部节点 c[x] 的值等于其子节点值的和
3. 每个内部节点 c[x] 的子节点个数为 lowbit(x) 的位数
4. 除树根外，每个内部节点 c[x] 的父节点为 c[x + lowbit(x)]
5. 树的深度为 O(log(n))，其中 n 表示 nums 数组的长度

总结一下，树状数组支持在 O(log(n)) 的时间复杂度内「求数组区间和」或「更新数组中某一点的值」，其完整代码如下所示：

int n; // 树状数组长度vector<int> c;int lowbit(x) {    return x & (-x);}void update(int x, int v) {    for (int i = x; i <= n; i += lowbit(i)) c[i] += v;}int query(int x) {    int res = 0;    for (int i = x; i; i -= lowbit(i)) res += c[i];    return res;}

习题练习

307. 区域和检索 - 数组可修改

题目描述

给你一个数组 nums ，请你完成两类查询，其中一类查询要求更新数组下标对应的值，另一类查询要求返回数组中某个范围内元素的总和。

实现 NumArray 类：

• NumArray(int[] nums) 用整数数组 nums 初始化对象
• void update(int index, int val) 将 nums[index] 的值更新为 val
• int sumRange(int left, int right) 返回子数组 nums[left, right] 的总和（即，nums[left] + nums[left + 1], ..., nums[right]）

示例

输入：["NumArray", "sumRange", "update", "sumRange"][[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]输出：[null, 9, null, 8]解释：NumArray numArray = new NumArray([1, 3, 5]);numArray.sumRange(0, 2); // 返回 9 ，sum([1,3,5]) = 9numArray.update(1, 2);   // nums = [1,2,5]numArray.sumRange(0, 2); // 返回 8 ，sum([1,2,5]) = 8

提示

• 1 <= nums.length <= 30000
• -100 <= nums[i] <= 100
• 0 <= index < nums.length
• -100 <= val <= 100
• 0 <= left <= right < nums.length
• 最多调用 30000 次 update 和 sumRange 方法

解题思路

该题属于树状数组的模板题，我们来依次查看其要实现的函数。

首先是用 nums 数组初始化树状数组 c，这时通常有两种操作，第一种是调用 n 次 update 函数，时间复杂度为 O(nlog(n))，代码如下：

for (int i = 1; i <= n; i++) update(i, nums[i]);

第二种是根据之前的树形结构，每一个内部节点 c[x] 的值等于其所有子节点值的和，因此可以实现 O(n) 时间复杂度内的初始化，代码如下：

for (int i = 1; i <= n; i++) {    c[i] += nums[i];    int j = i + lowbit(i);    if (j <= n) c[j] += c[i];}

接下来是第二个函数，将 nums[i] 的值更新为 val。而之前树状数组中的 update 操作为将 nums[i] 的值增加 val。因此我们需要「保存」或「求出」nums[i] 的当前值，再令其增加 val - nums[i] 即可。

最后是第三个函数，求 nums 数组在 [i, j] 上的区间和。之前树状数组的 query 操作可以求 [1, x] 的区间和，因此 [i, j] 的区间和等于 query(j) - query(i - 1)。

至此本题结束，具体代码如下。

代码实现

class NumArray {public:    int n;    vector<int> c;        int lowbit(int x) {        return x & (-x);    }        void update_c(int x, int v) {        for (int i = x; i <= n; i += lowbit(i)) c[i] += v;    }        int query(int x) {        int res = 0;        for (int i = x; i; i -= lowbit(i)) res += c[i];        return res;    }    NumArray(vector<int>& nums) {        n = nums.size();        c.clear();        c.resize(n + 1, 0);        for (int i = 1; i <= n; i++) {            c[i] += nums[i-1];            int j = i + lowbit(i);            if (j <= n) c[j] += c[i];        }    }        void update(int index, int val) {        val -= query(index + 1) - query(index);        update_c(index + 1, val);    }        int sumRange(int left, int right) {        return query(right + 1) - query(left);    }};

315. 计算右侧小于当前元素的个数

题目描述

给定一个整数数组 nums，按要求返回一个新数组 counts。数组 counts 有该性质：counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。

示例

输入：nums = [5,2,6,1]输出：[2,1,1,0] 解释：5 的右侧有 2 个更小的元素 (2 和 1)2 的右侧仅有 1 个更小的元素 (1)6 的右侧有 1 个更小的元素 (1)1 的右侧有 0 个更小的元素

提示

• 0 <= nums.length <= 100000
• -10000 <= nums[i] <= 10000

解题思路

该题与树状数组经典题「逆序对个数」相似，假设 (i, j) 为逆序对，则满足：

• i < j
• nums[i] > nums[j]

回到本题，题目要求 nums[i] 右侧小于它的元素个数。因此我们从右往左遍历 nums 数组，并且定义一个新数组 a，若遍历到 nums[i]，则令 a[nums[i]] = 1。

因此 counts[i] 即为数组 a 中 [-10000, nums[i] - 1] 的区间和。由于数组的下标为非负数，因此我们将 nums[i] 中所有数都加上 10001，将其原来的范围 [-10000, 10000] 移动到 [1, 20001]。

再用树状数组维护数组 a，即可完成此题，具体细节见下述代码。

代码实现

class Solution {public:    int n;    vector<int> c;    int lowbit(int x) {        return x & (-x);    }    void update(int x, int v) {        for (int i = x; i <= n; i += lowbit(i)) c[i] += v;    }    int query(int x) {        int res = 0;        for (int i = x; i; i -= lowbit(i)) res += c[i];        return res;    }    vector<int> countSmaller(vector<int>& nums) {        for (int i = 0; i < nums.size(); i++) nums[i] += 10001;        n = 2e4 + 1;        c.resize(n + 1, 0);        for (int i = nums.size() - 1; i >= 0; i--) {            int v = nums[i];            nums[i] = query(v - 1);            update(v, 1);        }        return nums;    }};

493. 翻转对

题目描述

给定一个数组 nums ，如果 i < j 且 nums[i] > 2 * nums[j] 我们就将 (i, j) 称作一个重要翻转对。

你需要返回给定数组中的重要翻转对的数量。

示例 1

输入: [1,3,2,3,1]输出: 2

示例 2

输入: [2,4,3,5,1]输出: 3

注意

• 给定数组的长度不会超过50000。
• 输入数组中的所有数字都在32位整数的表示范围内。

解题思路

该题与上题思路基本一致，上题要求的是：

• i < j
• nums[i] > nums[j]

但本题要求的是：

• i < j
• nums[i] > 2*nums[j]

因此我们依然可以从右往左遍历 nums 数组，并且定义一个新数组 a，若遍历到 nums[i]，则令 a[2 * nums[i]] = 1，即 update(2 * nums[i], 1)。

对于 i，求所有满足要求的 j，即为 query(nums[i] - 1)。

但本题还有一个关键点，即 nums[i] 的值可能很大，我们开不下这么大的空间。

每当遇到这种情况时，我们就需要采用「离散化」的手段。「离散化」的原理是将所有可能出现的数，如 2 * nums[i] 或 nums[i] 都存入数组，先排序再去除重复，然后再依次编号。

例如 nums[i] 原数组为 [1, 1, 1000000, 2]，则所有可能出现的数为 [1, 2, 1, 2, 1000000, 2000000, 2, 4]。将其排序，得到 [1, 1, 2, 2, 2, 4, 1000000, 2000000]。再去重得到 [1, 2, 4, 1000000, 2000000]。

因此我们可以将所有的 1 映射为 1，2 映射为 2，4 映射为 3，1000000 映射为 4，2000000 映射为 5。

由此树状数组的大小则不再取决于 nums[i] 的大小，而取决于 nums 数组的长度。

使用「离散化」的技巧，我们即可完成此题，具体细节见下述代码。

代码实现

class Solution {public:    int n;    vector<int> c;    int lowbit(int x) {        return x & (-x);    }    void update(int x, int v) {        for (int i = x; i <= n; i += lowbit(i)) c[i] += v;    }    int query(int x) {        int res = 0;        for (int i = x; i; i -= lowbit(i)) res += c[i];        return res;    }    int reversePairs(vector<int>& nums) {        // 离散化        set<long long> st;        unordered_map<long long, int> mp;        for (int i = 0; i < nums.size(); i++) {            st.insert(nums[i]);            st.insert(2ll * nums[i]);        }        int idx = 0;        for (auto x:st) mp[x] = ++idx;        n = idx;        c.resize(n + 1, 0);        // 求解        int ans = 0;        for (int i = nums.size() - 1; i >= 0; i--) {            ans += query(mp[nums[i]] - 1);            update(mp[2ll * nums[i]], 1);        }        return ans;    }};

总结

本文主要讲解了「树状数组」算法，该算法的核心功能为，能在 O(log(n)) 的时间复杂度内「求数组区间和」或者「更新数组中某一点的值」。

简单来说，如果遇到同时支持「求区间和」以及「单点操作」的数据结构题，则可以往「树状数组」的方向思考。

除此之外，该算法通过二进制的拆分，用 O(log(n)) 的效率代替了 O(n) 的简单做法，其算法思想也值得我们花时间好好理解。

本文作者：Gene_Liu

声明：本文归 “力扣” 版权所有，如需转载请联系。文中部分图片来源于网络，如有侵权联系删除。