数据结构与算法：从基础到高级的完全指南

二叉搜索树

大的在右边，小的在左边

缺点：无限插入一边元素，一直小，一直大，造成树的深度高，退化成链表

平衡二叉树—AVL树

左右子树的高度差不超过1(平衡因子)

1. 可以是空树。
2. 假如不是空树，任何一个结点的左子树与右子树都是平衡二叉树，并且高度之差的绝对值不超过 1。

旋转

平衡的调整共有四种情况：分别为LL,LR,RR,RL。

下面我们通过不断插入数据来说明几种不同的旋转方式:

• 左旋

• 右旋

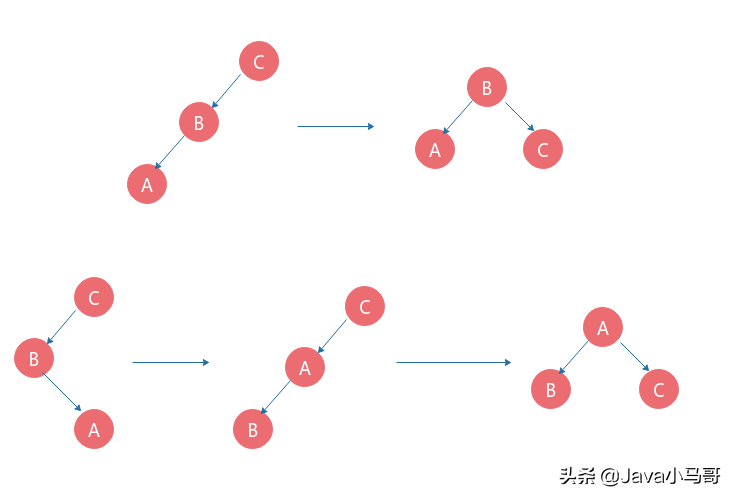
例子

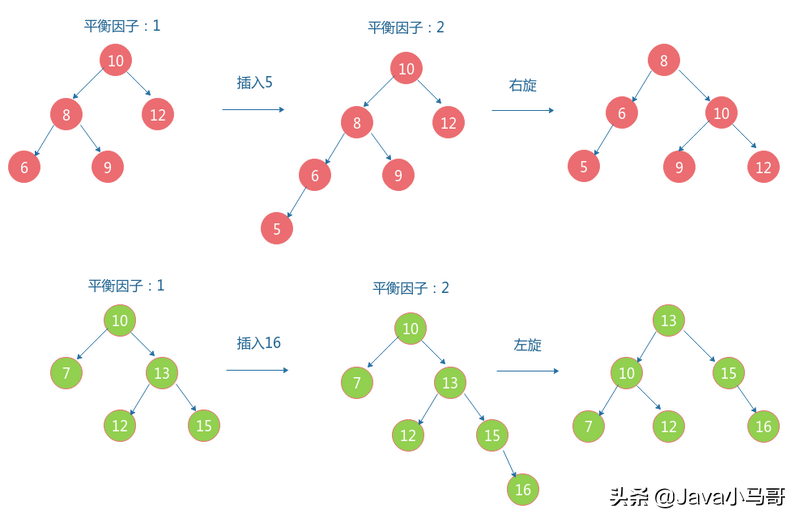
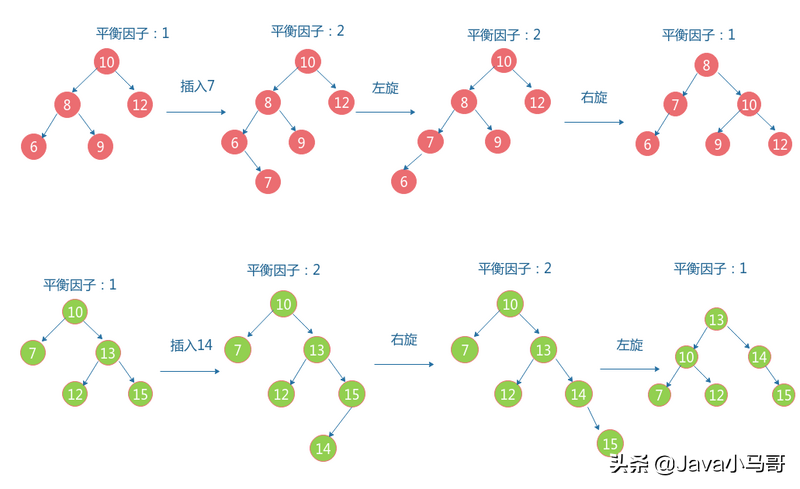
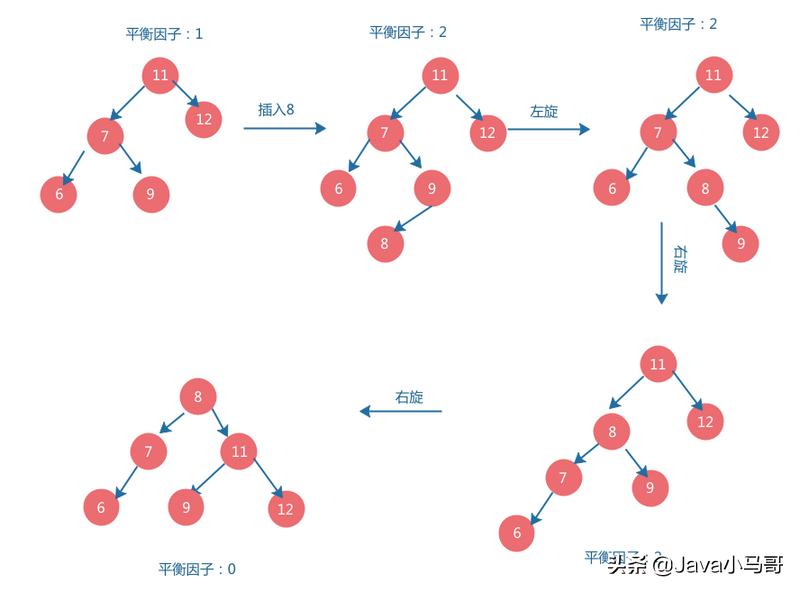
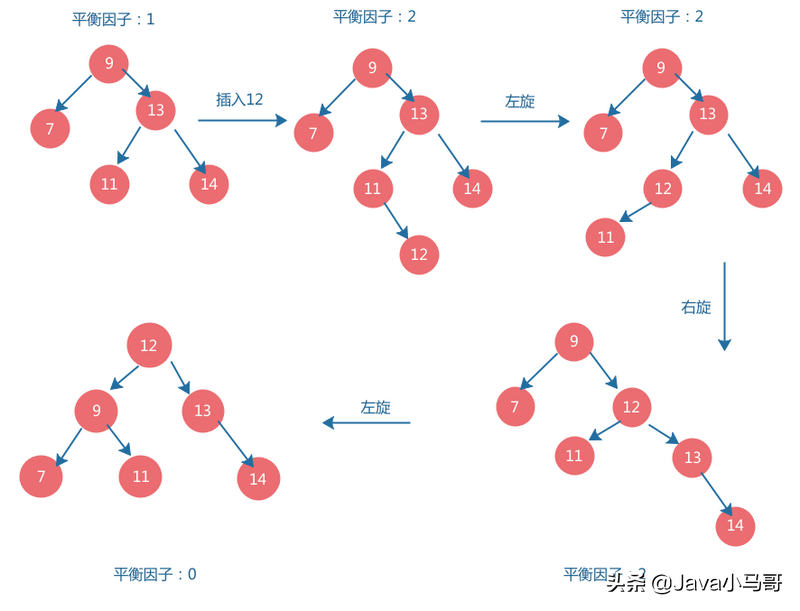
红黑树—RBT

Java8中红黑树、数据库索引、TreeMap、TreeSet，时间复杂度O(lgN)

自平衡二叉查找树

• 根节点必须黑色
• 叶子节点是黑色
• 父子不能同为红色
• 从任意节点出发，达到叶子节点经过的黑色节点数量一致

隐藏性质：

• 左右子树高度查最多为两倍

插入时默认插入红色，空的节点默认视为黑色(叶子节点)

修复规则：

根据插入情况应用处理策略调整，直到满足性质

• 旋转
• 变色

插入情况

1. 被插入节点是根节点处理：直接把其涂黑
2. 被插入节点父节点是黑色处理：直接插入，什么都不需要做
3. 被插入节点父节点是红色处理：这种情况我们分为下面三种Case，需要进行调整

• Case1：当前节点父节点和叔叔节点都是红色将父节点设置为黑色将叔叔节点设置为黑色将祖父节点设置为红色将祖父节点设置为当前节点，即继续对当前节点进行操作
• Case2：当前节点父节点是红色，叔叔节点是黑色，且当前节点是父节点的左孩子将父节点设置为黑色将祖父节点设置为红色以祖父节点为支点进行右旋
• Case3：当前节点父节点是红色，叔叔节点是黑色，且当前节点是父节点的右孩子当前结点的父结点做为新的当前结点以父节点为支点左旋得到Case2

例子：

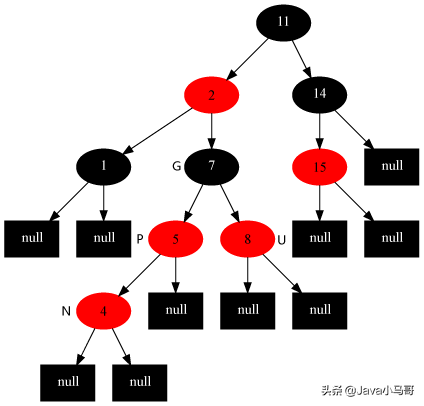
此时4节点处于Case1，执行处理

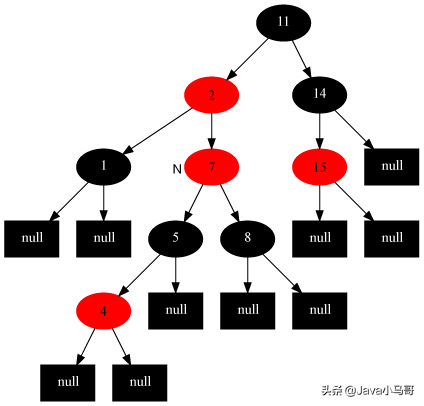
此时当前节点为7，处于Case3，执行处理

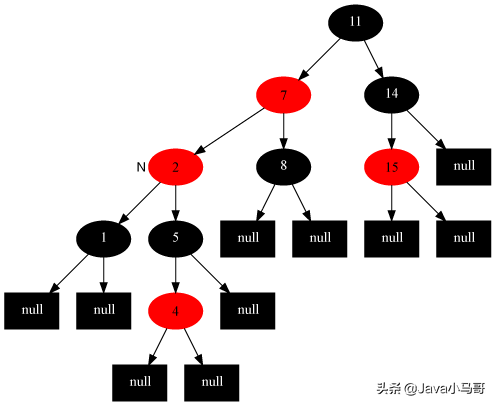
此时当前节点为2，处于Case2，执行处理

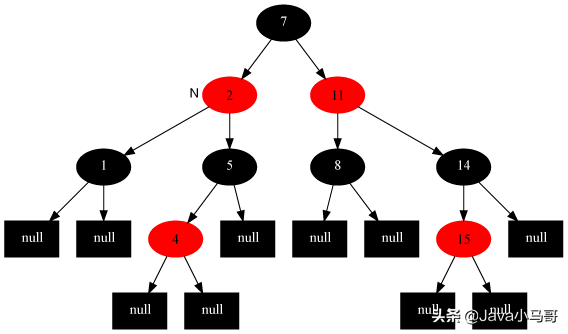
得到满足性质的红黑树