一. 诞生原因

找出存放一串字符所需的最少的二进制编码。

二. 构造方法

首先统计出每种字符出现的频率，即：概率、权值。

例如：频率表 A：60, B:45, C:13 D:69 E:14 F:5 G:3

第一步：找出字符中频率最小的两个，小的在左边，大的在右边，组成二叉树。在频率表中删除此次找到的两个数，并加入此次最小两个数的频率和。

F 和 G 最小，如下图所示，从字符串频率计数中删除 F 与 G，并返回 G 与 F 的和 8 给频率表。

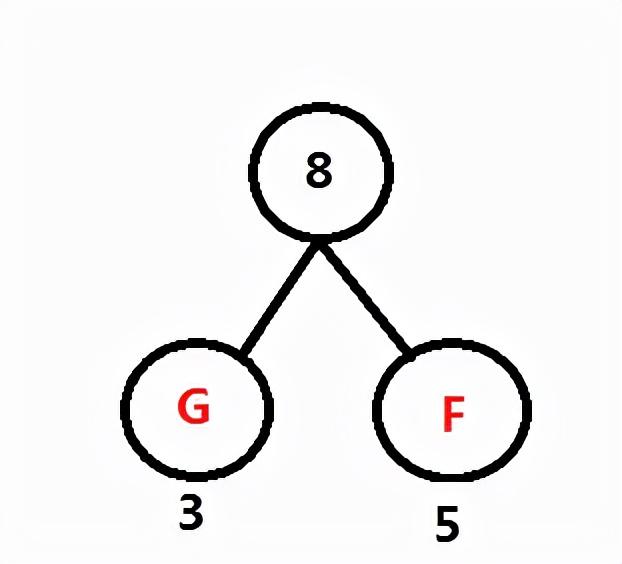
第二步：频率表 A：60, B:45, C:13 D:69 E:14 FG:8

频率最小的是 FG：8 与 C：13，如下图所示，并返回 FGC 的和 21 给频率表。

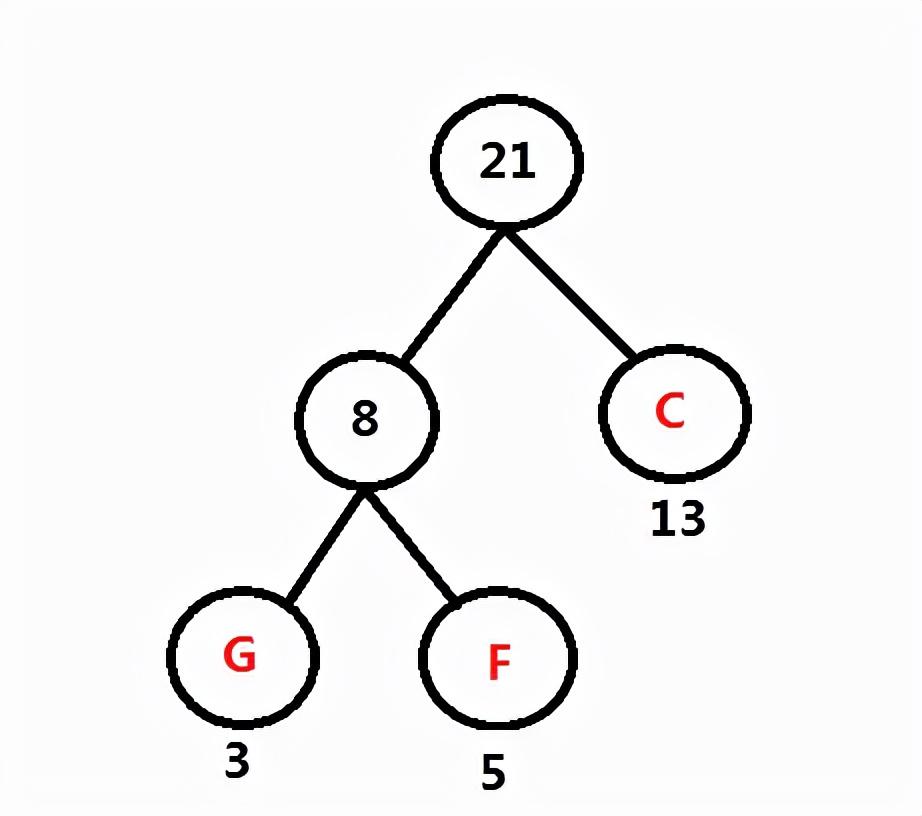
第三步：频率表 A：60 B: 45 D: 69 E: 14 FGC: 21

如图

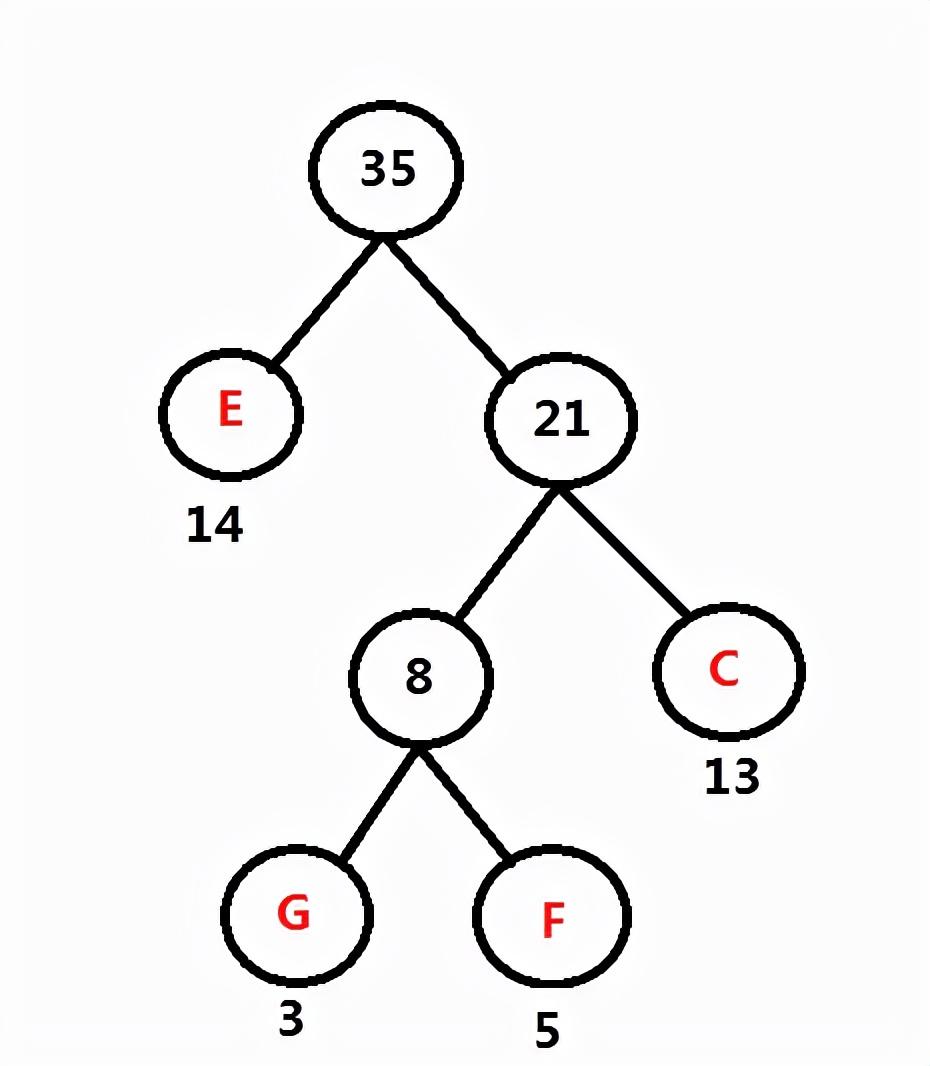
频率表 A：60 B: 45 D: 69 FGCE: 35

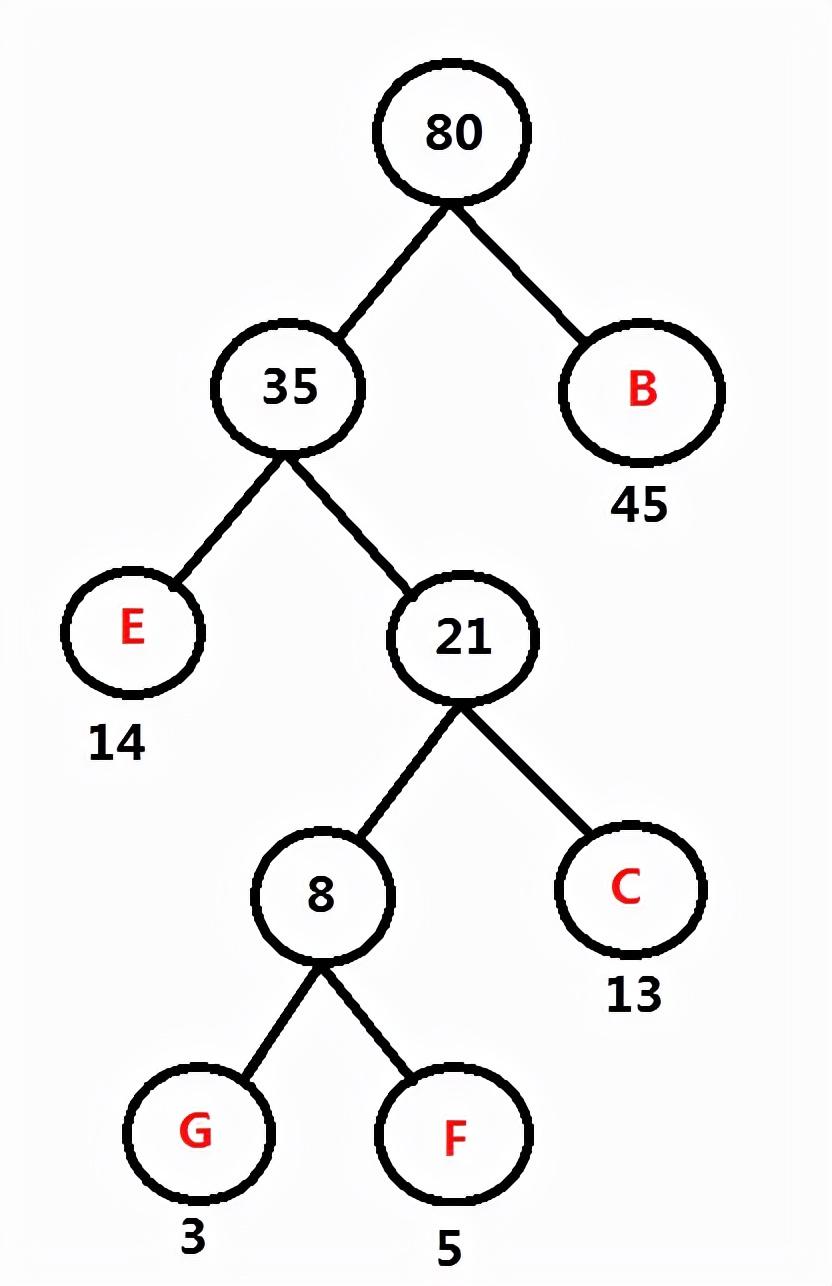
频率表 A：60 D: 69 FGCEB: 80

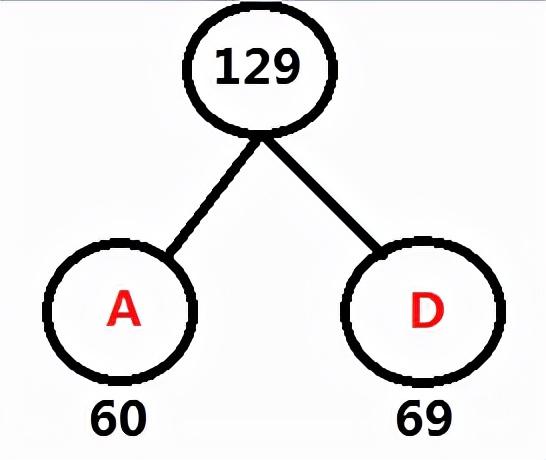
频率表 AD：129 FGCEB: 80

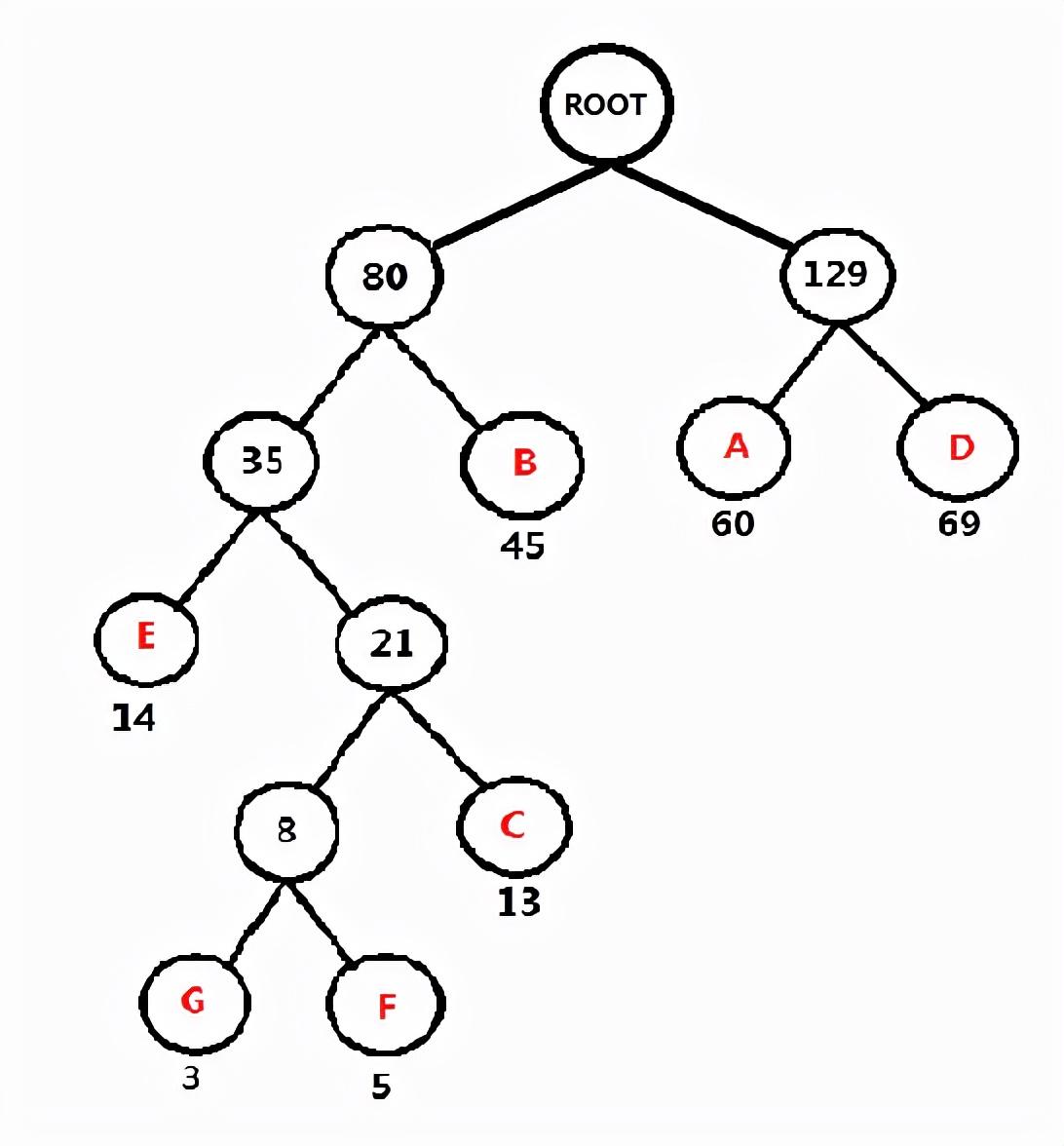
添加 0 和 1，规则左 0 右 1 。

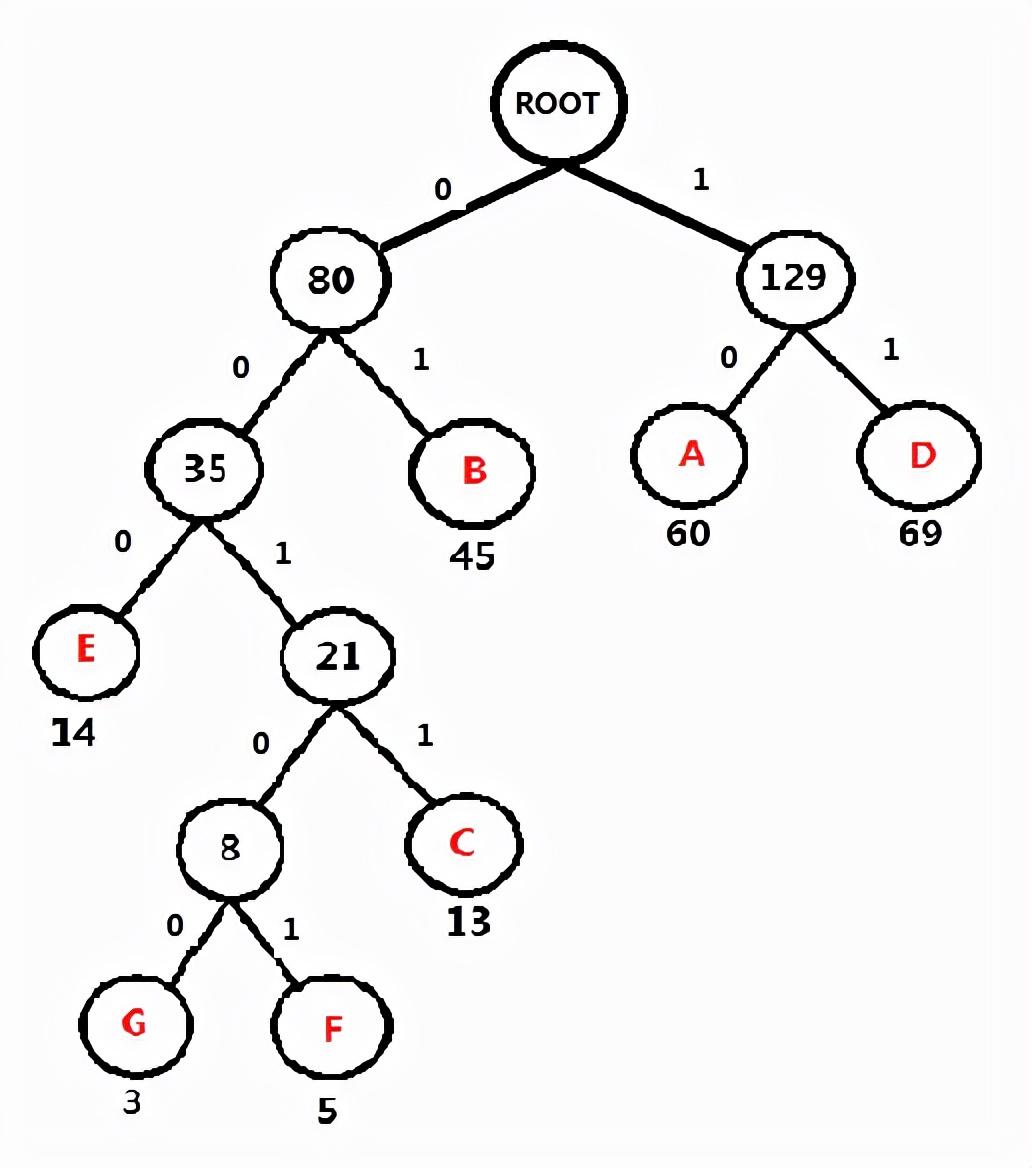
频率表 A：60, B:45, C:13 D:69 E:14 F:5 G:3

每个字符的二进制编码为（从根节点到对应的叶子节点，路径上的值拼接起来就是叶子节点字母的应该的编码）

那么当我想传送 ABC 时，编码为 10 01 0011，该编码就是 霍夫曼编码 。

对于解码操作来说，编码接收方同时接收到编码中对应的字符列表以及各个字符的概率值，重新建立霍夫曼树，从而根据编码每次从树的根遍历至树的叶子节点，最终还原整个字符串。

三、总结

1、出现得越多的字母，他的编码越短 ；出现频率越少的字母，他的编码越长。

在信息传输过程中，如果这个字母越多，那么我们希望他越瘦小（编码短）这样占用的编码越少，其实编码长的字母也是让频率比它多的字母把编码短的位子都占用后，他才去占用当前最短的编码。至此让总的编码长度最短。

实际上这就是贪心算法。

2、保证长编码的不与短编码的字母冲突。

比如不能出现读码读到 01 还有长编码的字母为 011，如果短编码为一个长编码的左起子串，这就是冲突，意思就是说读到当前位置已经能确定是什么字母时不能因为再读取一位或几位让这个编码能表示另外的字母。

哈夫曼树（最优二叉树）在构造的时候避免了这个问题。为什么能避免呢，因为哈夫曼树的它的字母都在叶子节点上，因此不会出现一个字母的编码为另一个字母编码左起子串的情况。

3、霍夫曼树不是唯一的。

同一字符串，可以构建出不同的霍夫曼树，例如将上例的构建规则改为频率较低的放在右边，频率较高的放在左边，这样构建的树就不同了。总的来说这叫同权不同构。

四、应用场景

典型的应用场景就是数据压缩，压缩一个 txt 文件，将其二进制转成 Base 64 编码，对该编码串建立霍夫曼树，从而可以得到霍夫曼编码。该编码相对于原 Base 64 串来说体积小很多，从而达到了数据压缩的目的。

五、其他

在实际编码过程中，如何快速找到频率表中最小的两个值呢，这里可以采用 堆结构 来实现。