【CSDN 编者按】这是一只小猫的经历,本文不同以往的风格,采用新奇的三人称视角来探究 Python 与数学之间的奥秘~
引子
我是一只猫。听起来有点惊悚,但这是千真万确的事实。
那一年——这样说,并不一定意味着一个历史故事的开始,因为我没有过去和将来的概念。我可以在时间维度上任意移动,就像从东走到西或者从西走到东那样自然。
那一年,应该是公元 1963 年。当时我正在美国阿拉莫斯国家试验室的一间会议室的窗台上享受着温暖的午后秋阳,会议室里一群人正在开会。这里处于新墨西哥州杰姆斯山森林的包围之中,空气清新且日照充足,因此我经常从欧洲或者亚洲来这里度假。
会议主题冗长且毫无新意,有些听众开始打起了哈欠。期间,有个一直埋头写写画画的家伙引起了我的注意。他叫乌拉姆,波兰裔物理学家和数学家,我很早就认识他。
乌拉姆在这间国家实验室的最大成就,是和氢弹之父泰勒合作提出泰勒-乌拉姆设计(Teller–Ulam design),为核聚变武器研发提供了基础支撑,并最终导致第一颗氢弹的成功试爆。
灵光乍现
“喵——”
我悄悄走到乌拉姆身后,打了一个招呼,用胡须轻轻碰了一下乌拉姆右侧的面颊。乌拉姆先用左手拍了拍趴在肩头的我,然后回过头来。
“嘘——小声点。你知道吗,我可能发现了一个天大的秘密,这绝对比泰勒-乌拉姆设计更有意义。让泰勒那个讨厌的家伙见鬼去吧。”
乌拉姆面色潮红,两眼放光,看起来有点亢奋。“曼哈顿计划”计划之后,由于内心抗拒继续研制热核武器,乌拉姆在氢弹研制中几乎被人遗忘,心里多少有一点忿忿不平。
“哦?说来听听。”
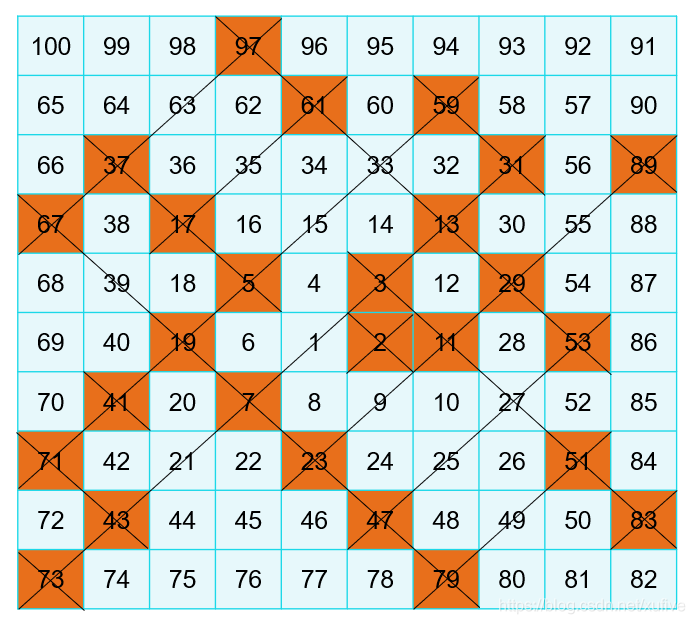
“你看,从 1 开始,逆时针转圈将连续的整数写在 10x10 的格子里。”乌拉姆拿起桌上的那张草纸,右手食指指向中间位置,然后开始转圈。纸上是他画的方格、数字和斜线,就像下图这个样子。
乌拉姆手绘的100以内的素数分布图(10x10)
“把其中的素数用红笔标上颜色,我突然发现,这些素数居然都出现在斜线上!”
这时我才明白,乌拉姆为什么会如此激动了。千百年来,从古希腊的欧几里得、古埃及的埃拉托色尼,到近代德国的高斯和黎曼、法国的勒让德,人类一直在尝试解决素数的多少以及如何分布的问题,并试图找到一个可以计算出所有素数的简单公式。尽管这些数学天才们穷尽了可能的手段,但是并没有得到期望的结果。乌拉姆也许觉得自己找到了素数的分布规律。
“这只是 100 以内的素数,说明不了什么吧?”
“是的,这张草纸太小了。要是给我一张足够大的纸,也许可以从中发现什么。”
“是个好主意。不过,一个数字一个数字的填写,效率太低了。为什么不试试 Python 呢?”
在那一瞬间,忽然想起来我在北大混日子的时光。那时候,人们喜欢叫我哲学猫。其实,除了喜欢旁听哲学和艺术,我偶尔也去听听计算机课,在那里,我多少了解了一点 Python 的知识。
“Python?蟒蛇也研究数学吗?”
看着乌拉姆一脸懵逼,我意识到自己犯了一个错误:Python 直到 1989 年才诞生,那时乌拉姆已经去世五年了。想到这一点,我心里微微有一些伤感。
“这是很多年后一个名叫吉多·范罗苏姆的荷兰人搞出来的编程语言,可以协助处理一些重复的、繁琐的事务性工作。这个语言最初无人问津,没想到几十年后却风靡全球,火得烫手。没关系,我可以提前拿来用一下,帮你搞搞这个。”我指了一下他画的草图。
对于我能从未来临时借用 Pyhton,乌拉姆并未表现出任何的惊奇或不解。这倒不是因为他是顶尖的物理学家,可以理解四维生物的生存状态,而是早在我协助薛定谔做量子实验的时候,他就已经认识我了。薛定谔是奥地利人,乌拉姆生于波兰,从格拉茨开车到华沙只有 800 公里。这段距离,搁在中国就算是同乡了,加上又是同行,尽管年龄相差二十几岁,两人却是忘年之交。
乌拉姆现象
“这是全美目前最快的电脑,每秒钟可以完成 3000 次计算。”
乌拉姆将我带进机房,指着一台美国数据设备公司(DEC)生产的 POP-5 小型机说。
“你这里,也许只有电源是可用的。”
我苦笑一下,打开了自己的电脑,边敲键盘,边和正在背身操作咖啡机的乌拉姆讨论如何绘制素数分布图。
“我打算这样做:先搞一个可以计算 n 以内素数的函数,再搞一个将 1 到 n 逆时针转圈排列成生成方阵的函数。调用这两个函数,分别得到素数表和数字方阵,然后将方阵中的素数置为 255,合数置为 0……”
“哇呜,这主意听起来相当美妙!最后得到一张灰度图,白色像素点表示素数,黑色像素点表示合数,素数的分布规律——如果有的话,就会一目了然。”
这家伙脑子的确好使,没上过计算机课,也能搞得门儿清。我抬头斜着眼瞅了乌拉姆一下,他知趣地用咖啡杯堵住了嘴。
既然他都明白了,就不用继续说我的计划了,直接写代码吧。先把需要的模块导入。万一要是没有安装所需模块,还得回到几十年后才能找到可用的模块。
import numpy as npfrom PIL import Image
幸好我的电脑上早已安装了 NumPy 和 pillow 这两个模块,开局非常顺利。再定义一个函数,找出不大于 n 的所有素数。
def find_prime_list(n):"""返回不大于n的素数组成的numpy数组"""nums = np.arange(n+1) # 生成0到n的数组nums[1] = 0 # 数组第1和元素置0,从2开始,都是非0的k, m = 0, pow(n+1, 0.5)while True: # 循环primes = nums[nums>0] # 找出所有非0的元素if primes.any(): # 如果存在不为0的元素p = primes[k] # 则第一个元素为素数k += 1nums[2*p::p] = 0 # 这个素数的所有倍数,都置为0if p > m: # 如果找到的素数大于上限的平方根break # 则退出循环else:break # 全部0,也退出循环return nums[nums>0]
将1到n逆时针转圈排列成生成方阵,稍微有点一点难度。看我想得出神,乌拉姆建议说:“为了简化设计,我们可以限定 n 必须是一个平方数,这样最终得到的方阵的行列数都是 n 的算术平方根,你写程序也容易一点。”
我接受了乌拉姆的建议。有了这个约束条件,思路一下就清晰了:假定 n 的算术平方根为 side,不考虑效率的话,可以先生成一个 side*side 的二维列表,其元素全部为 None;如果 side 为奇数,则 n 位于二维列表的右下角,n-1 位于 n 的左侧,否则,n 位于二维列表的左上角,n-1位于n的右侧;然后从 n开始逆序将数字按照顺时针方向写入列表。
def get_square(n):"""将从1开始的n个连续的整数排成一个列表"""side = int(pow(n, 1/2)) # 方阵边长if side%2:row, col = side-1, side-1direct = 'left'else:row, col = 0, 0direct = 'right'result = [[None for j in range(side)] for i in range(side)]for i in range(n, 0, -1):result[row][col] = iif direct == 'right':if col+1 == side or result[row][col+1]: # 如果不能继续向右,则向下:row += 1direct = 'down'else: # 否则继续向右col += 1elif direct == 'down':if row+1 == side or result[row+1][col]: # 如果不能继续向下,则向左col -= 1direct = 'left'else: # 否则继续向下row += 1elif direct == 'left':if col-1 < 0 or result[row][col-1]: # 如果不能继续向左,则向上row -= 1direct = 'up'else: # 否则继续向左col -= 1elif direct == 'up':if row-1 < 0 or result[row-1][col]: # 如果不能继续向上,则向右col += 1direct = 'right'else: # 否则继续向上row -= 1return np.array(result)
有了素数表,有了方阵,只剩下替换操作,就简单多了。
def plot_prime(side):"""绘制不大于side*side的质数分布图"""n = side * sidesquare = get_square(n)primes = find_prime_list(n)im_arr = np.isin(square, primes).astype(np.uint8) * 255im = Image.fromarray(im_arr)im.save('%dx%d.jpg'%(side, side))
写到这里的时候,我抬起头,注意到乌拉姆一脸惊讶的表情。
“这个方阵里的素数是怎么被替换成 255 的?我无法理解 np.isin()这个神奇的东西。感觉创造 Python 的那个荷兰人,智商比爱因斯坦还高!”
乌拉姆平生最服气爱因斯坦,一旦遇到牛人,总喜欢和爱因斯坦作比较。
“哦,你说的是 NumPy,那的确是一个很牛叉的东西。不过你不用因此而自卑,NumPy 不是吉多·范罗苏姆写的,而是由一个伟大的团队研发的。”
“我就说嘛,这怎么可能是一个人的力量可以做到的呢。其实大家都明白,氢弹也不是泰勒那家伙一个人搞出来的。”
看来乌拉姆对于泰勒贪功一事一直无法释怀。我没有接乌勒姆的话茬,而是转向笔记本电脑,开始了第一次的运行测试。先从 100x100 的方阵开始。
plot_prime(100)运行结束,打开图片之前,乌拉姆的右手一直放在我的后背上。我能感觉到他的紧张和期待。看到图片的时候,他先是盯着看了三秒钟,然后双手猛然击掌,兴奋地大喊:“果然存在斜线!快,再来几张更大的。”
代码运行效率比想象的要好很多,轻松生成了 9 万、36 万和 100 万以内的素数分布图。
plot_prime(300)plot_prime(600)plot_prime(1000)
现在我一点儿都不担心乌拉姆会提出更大的要求,因为这个速度已经远远超出了全世界的计算机算力。而乌拉姆没有想到,他无意中发现了被后人称为“乌拉姆现象”的素数分布特点。
9万以内的素数分布图(300x300)
36万以内的素数分布图(600x600)
1百万以内的素数分布图(1000x1000)
悖论
短暂的激动之后,乌拉姆盯着这张 1 百万以内的素数分布图,陷入了沉思。良久,他开口说话了。
“能否再帮我算一下 1 千万内和 1 亿以内的素数的个数?”
“当然。”
我把查找素数的函数 find_prime_list()稍微改造了一下,将查找范围分成多个区块。这样做主要是为了降低内存消耗,另外也便于并行计算——实际上我并没有启用并行计算,因为逐个区块计算就已经足够快了。
---------------------------------查找10000000以内的素数耗时0.365秒共找到664579个素数---------------------------------查找1亿以内的素数耗时2.862秒共找到5761455个素数
乌拉姆瞅了一眼屏幕,低头在一张草纸上写下了这样一个公式。
“这里的 π \piπ 可不是圆周率,而是表示不大于自然数 x xx 的素数的个数。”他左手端起早已凉透的半杯咖啡,用右手中指的关节轻扣草纸。
“欧拉和勒让德早已证明了当 x xx 趋于无穷大时,π ( x ) \pi(x)π(x)与 x xx 之比等于0——这意味,即便素数有无穷多个,也不应该出现在自然数中,因为素数在自然数中出现的概率为0。”
“这可真是一个有趣的悖论。”
我不知道乌拉姆要表达什么,只好敷衍地回应了一句。
沉默有顷,乌拉姆幽幽地说:"Python 在几秒钟内就可以计算出,当 x xx 趋近1亿时,素数出现的概率降低到 5.76%。这是一个强大的工具,可以瞬间完成单凭人力无法完成的计算任务,但是,却剥夺了人类享受在黑暗中探索和思考的乐趣。”
“伸手不见五指,没有方向,没有终点,那不是痛苦吗?”
“不,那是一种享受。天堂向左,数学向右。”
“好吧,我想我能理解你的意思。时间的不可逆,和对时光逆转的渴望,令人类创造了一些有趣的概念,比如天堂,还有 Python。为什么不是 Python 向左,数学向右呢,乌拉姆博士?”









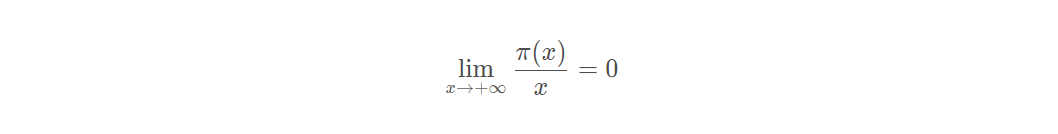
 鲁公网安备37020202000738号
鲁公网安备37020202000738号