探索数据结构与算法：复杂度的奥秘

算法是用于解决特定问题的一系列的执行步骤。使用不同算法，解决同一个问题，效率可能相差非常大。为了对算法的好坏进行评价，我们引入 “算法复杂度” 的概念。

1、引例：斐波那契数列（Fibonacci sequence）

已知斐波那契数列： ，求它的通项公式 。

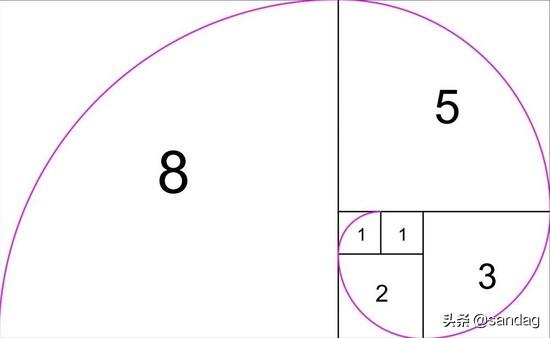
求解斐波那契数列的方法有很多种，这里只介绍两种：递归法和平推法。

package com.atangbiji;public class Main {	public static void main(String[] args) {		// 输出通项F(n)		System.out.println(fib1(1));		System.out.println(fib1(2));		System.out.println(fib1(3));		System.out.println(fib1(4));		System.out.println(fib1(5));				System.out.println(fib2(70));	}		/*	 * 求斐波那契数列（Fibonacci sequence）	 * F(1)=1，F(2)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 3，n ∈ N*）的通项F(n).	 */		/*	 *  方法一：递归法	 *  最高支持 n = 92 ，否则超出 Long.MAX_VALUE	 * @param n 	 * @return f(n) 	 * */		public static long fib1(int n) {		if (n < 1 || n > 92)	        return 0;		if (n < 3)			return 1;				return fib1(n - 1) + fib1(n - 2);	}		/*	 *  方法二：平推法	 *  最高支持 n = 92 ，否则超出 Long.MAX_VALUE	 * @param n 	 * @return f(n) 	 * */	public static long fib2(int n) {		if (n < 1 || n > 92)	        return 0;		//n:    1 2 3 4 5 ……		//F(n): 1 1 2 3 5 ……		long first = 1;		long second = 1;		for (int i = 3; i <= n; i++) {			long sum = first + second;			first = second;			second = sum;		}		return second;	}}

通过测试，我们可以发现：当n的取值较大时（如：n = 60），若采用递推法计算则会发现迟迟不出结果，若采用平推法计算则可以秒出结果。由此可见， 平推法的效率明显高于递推法。

2、如何评估算法的好坏？

• 正确性
• 可读性
• 健壮性：对不合理输入的反应能力和处理能力。
• 时间复杂度（time complexity）： 估算程序指令的执行次数（执行时间）。
• 空间复杂度（space complexity）： 估算所需占用的存储空间。

注： 一般情况下，我们主要考虑算法的时间复杂度。 （因为目前计算机的内存一般都比较大）

3、时间复杂度的估算

我们可以用程序指令的执行次数来估算时间复杂度。例如：

（1）函数test1

public static void test1(int n) {	//总执行次数 = 14		// 1（判断语句可以忽略）	if (n > 10) {		System.out.println("n > 10");	} else if (n > 5) {		System.out.println("n > 5");	} else {		System.out.println("n <= 5");	}		// 1 + 4 + 4 + 4	for (int i = 0; i < 4; i++) {		System.out.println("test");	}}

（2）函数test2

public static void test2(int n) {	//总执行次数 = 1 + 3n		//1 + n + n + n	for (int i = 0; i < n; i++) {		System.out.println("test");	}}

（3）函数test3

public static void test3(int n) {	//总执行次数 = 48n + 1		// 1 + 2n + n * (1 + 45)	for (int i = 0; i < n; i++) {		for (int j = 0; j < 15; j++) { // 1 + 15 + 15 + 15			System.out.println("test");		}	}}

（4）函数test4

public static void test4(int n) {	//总执行次数 = 3n^2 +3n +1		// 1 + 2n + n * (1 + 3n)	for (int i = 0; i < n; i++) {		for (int j = 0; j < n; j++) { // 1 + n + n + n			System.out.println("test");		}	}}

（5）★ 函数test5

public static void test5(int n) {	//总执行次数 = log2(n)		/*	 * n = 2 , 执行 1 次	 * n = 4 , 执行 2 次	 * n = 8 , 执行 3 次 	 * */	while ((n = n/2) > 0) { // 倍速减小		System.out.println("test"); // 只考虑这一句的执行次数	}}

（6）函数test6

public static void test6(int n) {	//总执行次数 = log5(n)	while ((n = n/5) > 0) {		System.out.println("test"); // 只考虑这一句的执行次数	}}

（7）函数test7

public static void test7(int n) {	//总执行次数 = 3n*log2(n) + 3log2(n) + 1		// 1 + 2 * log2(n) + log2(n) * (1 + 3n)	/*	 * n = 2 , 执行 1 次	 * n = 4 , 执行 2 次	 * n = 8 , 执行 3 次 	 * */	for (int i = 1; i < n; i += i) { // i = i + i = i * 2（倍速增大）		for (int j = 0; j < n; j++) { // 1 + n + n + n			System.out.println("test");		}	}}

4、大O表示法

为了进一步简化复杂度的计算，我们一般使用大O表示法来描述时间（或空间）复杂度。它表示的是 数据规模为n 时算法所对应的复杂度。

大O表示法的性质：

（1）可以忽略常数、常系数和低阶项。

（2）对数阶一般省略底数，统称 。

注： 大O表示法仅仅只是一种粗略的分析模型，是一种估算。 它能帮我们快速了解一个算法的执行效率。

5、常见的复杂度

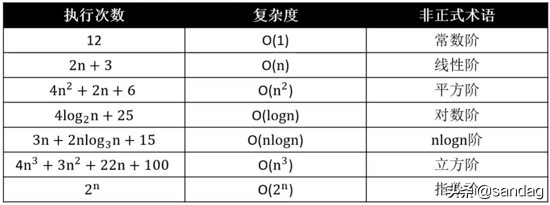
其中：

• 当数据规模较小时，各复杂度对应的曲线如下图所示。
• 当数据规模较大时，各复杂度对应的曲线如下图所示。

所以，当数据规模比较大时，复杂度为 我们就很难接受了。

6、斐波那契数算法复杂度分析

（1）递归法

public static long fib1(int n) {	if (n < 1 || n > 92)        return 0;	if (n < 3)		return 1;		return fib1(n - 1) + fib1(n - 2);}

假设计算 时 和 的值已经得到，我们可以发现该函数每次执行的时间主要取决于求和运算。因此，该算法函数指令的执行次数等价于该函数被递归调用次数。

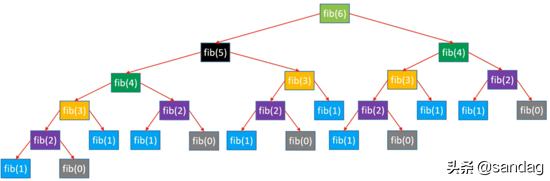
当 时，该函数的调用过程如下图所示。

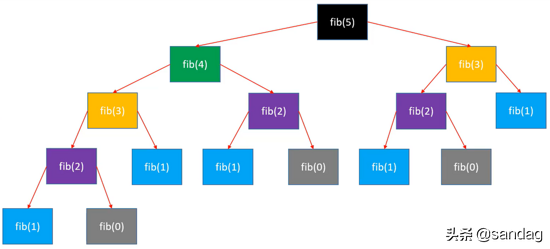
所以，该函数被递归调用的次数 二叉树的节点数。

即： 。

因此，该算法的复杂度为 。

**注：**细心的同学可能会发现，当 时，函数被递归调用的次数并不完全等于 。

这里需要说明的是： 复杂度是一种估算，我们关心的不是具体的数值，而是量级和趋势。 所以， 呈指数级增长的趋势是毋庸置疑的。

（2）平推法

public static long fib2(int n) {	if (n < 1 || n > 92)        return 0;	//n:    1 2 3 4 5 ……	//F(n): 1 1 2 3 5 ……	long first = 1;	long second = 1;	for (int i = 3; i <= n; i++) {		long sum = first + second;		first = second;		second = sum;	}	return second;}

显然，平推法的时间复杂度为 。

7、算法的优化方向

（1）用尽量少的执行步骤（运行时间）。

（2）用尽量少的存储空间。

（3）根据情况，空间换时间或者时间换空间。

更多关于复杂度的知识，我们会在后续数据结构和算法的设计与实现过程中穿插讲解。

参考文献： [1] 《恋上数据结构与算法》，小码哥MJ [2] 《数据结构与算法》，邓俊辉