
一、数据结构和算法
数据结构:元素之间的关系,分为逻辑结构和存储结构。
1. 逻辑结构
(1)线性结构
每个元素前、后最多都只能有一个节点,如:线性表、栈、队列、数组、串
(2)非线性结构
如:二维数组、多维数组、树、图等
2. 存储结构
- 顺序存储
- 链接存储
3. 顺序表
含有n个元素的线性表采用顺序存储,等概率删除其中任一个元素,平均需要移动n − 1 2 \frac{n-1}数据结构和算法2n−1个元素。
4. 链表
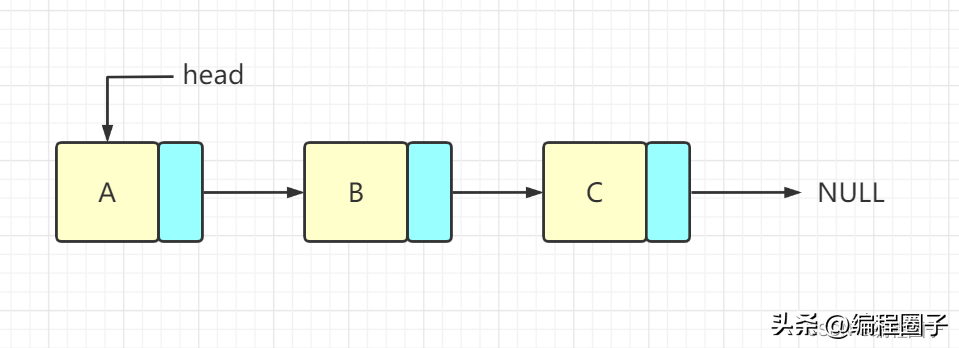
链表中的每个元素称为结点,每个结束是一个结构体变量,分为:
- 数据部分
- 指针变量:通常具有指向自身结构体类型的指针变量,存放下一结点的地址,最后一个结点的地址为NULL(单链表)。
- 尾结束:最后一个结点
- 尾指针:找尾结点的指针
- 头结点:第一个结点
- 头指针:指向头结点的指针变量
- 首结点:第一个有效结点
- 循环链表,尾指针指向头结点地址。
- 双向链表:每个结点增加一个front用来存放前一个结点地址。
二、数组和字符串
数组:表示n个数据类型相同的元素所组成的序列。
字符串:字符构成的一维数组。
- 空串: 没有任何字符
- 空白串:字符都是不可见的
- 子串:串中任意个连续的字符组成的子序列
- 非平凡子串:非空且不同于字符串本身
- 串的模式匹配:模式串在主串中首次出现的位置
- 字符串的比较:从左到右按ASCIID码值进行比较
三、矩阵
1. 特殊矩阵
- 三角矩阵:上三角矩阵、下三角矩阵(存非零元素即可)。
- 对角矩阵
- 对称矩阵:A i j = A j i A_{ij}=A_{ji}Aij=Aji
- 反对称矩阵:A i j = − A j i A_{ij}=-A_{ji}Aij=−Aji
2. 非特殊矩阵
- 稀疏矩阵:使用三元组存储
3. 矩阵乘法
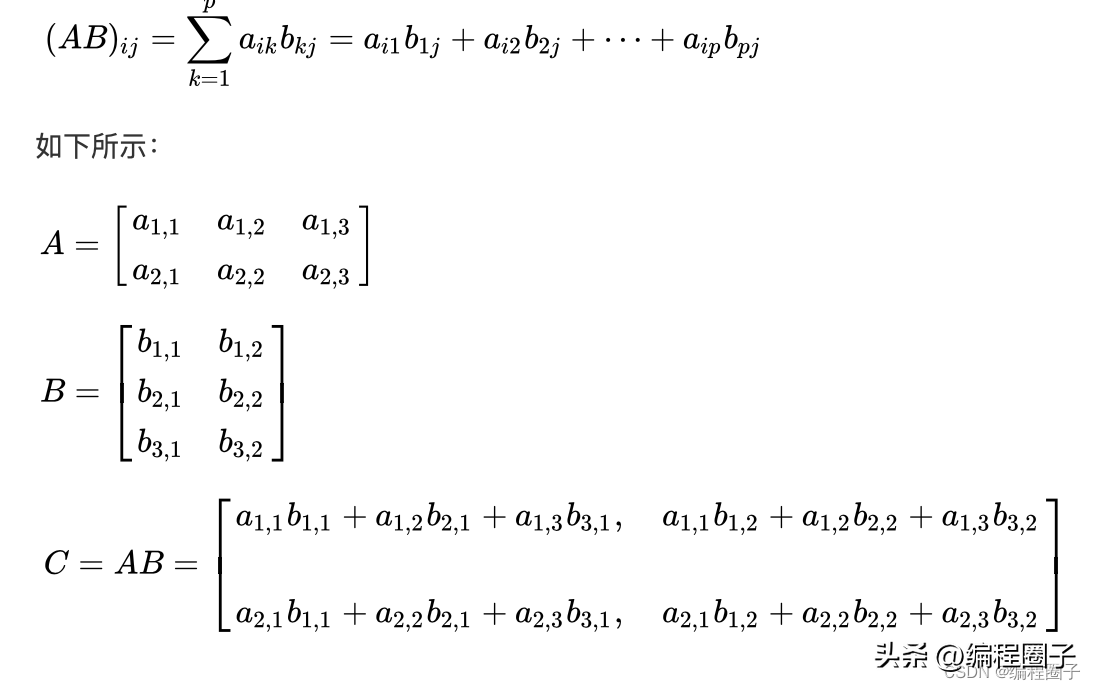
三、栈和队列
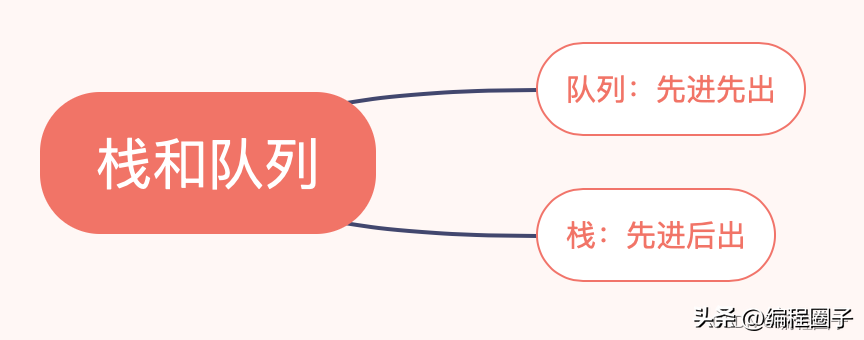
1. 队列(先进先出,FIFO——first in first out)
- 队尾: rear
- 队头:front
2. 栈(先进后出,FILO——first in last out)
四、树
1. 树的基本概念
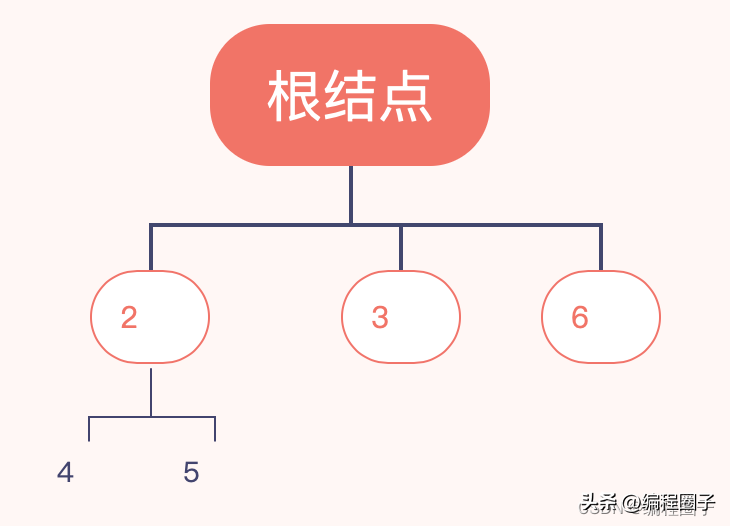
- 父结点
- 子结点
- 兄弟结点
- 叶子结点:没有子结点
- 结点的度:结点有几个子结点
- 树的度:所有结点度最大的值
- 二叉树:树的度不超过2
- 层(深度、高度)
2. 二叉树
(1)一些概念
满二叉树
每一层都不能增加结点
完全二叉树
除了最后一层,都不能增加结点。 最后一层左侧连续有,右侧连续无。
非完全二叉树
除了最后一层,都不能增加结点。但不满足最后一层左侧连续有、右侧连续无的条件 。
(2)二叉树的特性
- 每一层上最多有2 n − 1 2^{n-1}2n−1个节点
- 深度为k的二叉树最多有2 k − 1 2_k-12k−1个节点
- 如果对一棵有n个结点的完全二叉树的结点按层序编号,有:
如果i=1,则结点i无父结点,二叉树的根;如果i>1,则父结点是 i/2取整。
如果2i>n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i。
如果2i+1>n,则结点i无右子结点,否则,其右子结点是结点2i+1。
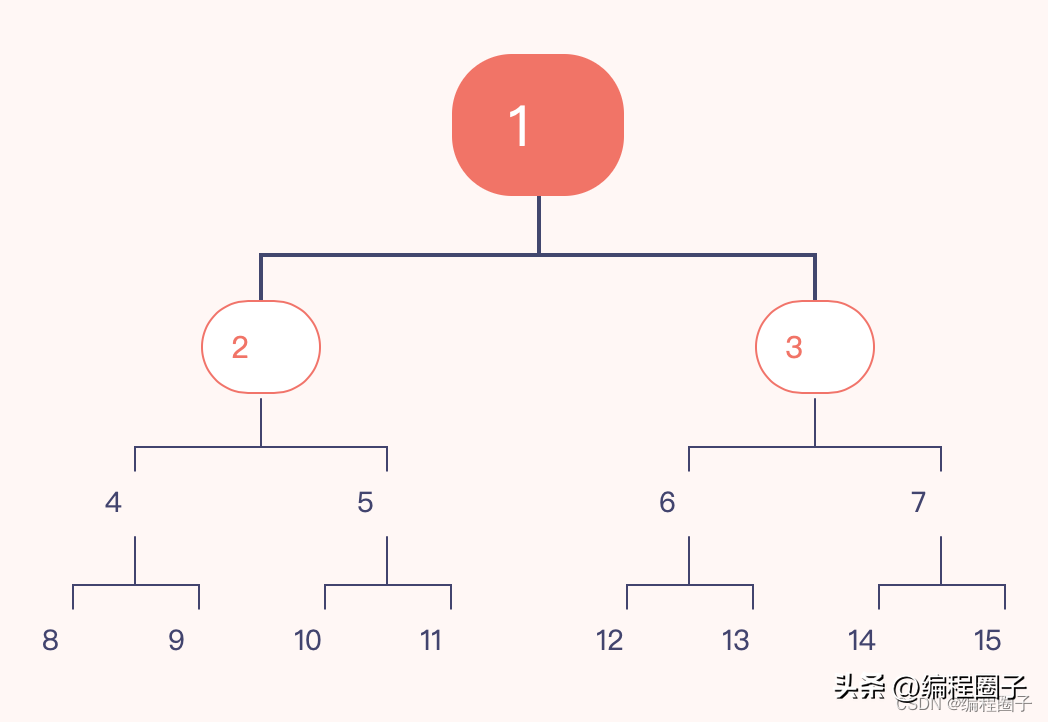
3. 树的遍历
- 前序/先序遍历
- 中序遍历
- 后序遍历
- 层序遍历
4. 特殊二叉树
(1) 二叉排序树
- 二叉排序/查找树
- 左子树小于根
- 右子树大于根
值最小的结点无左子树
值最大的结点无右子树。
二叉查找树的中序遍历序列为从小到大排列的序列
每一层从左到右进行遍历的序列为从小到大排列的序列。
(2) 哈夫曼树
- 树的路径长度:从树根到树中每一结点的长度之路
- 权:在一些应用中,赋予树中结点的一个有特定含义的数
- 带权路径长度:结点到树根之间的路径长度与该结点上权的乘积
- 树的代价:树的带权路径长度
- 哈夫曼树的构造
五、图
1. 图的分类
(1)有向图
一个顶点到另一个顶点是有方向的;
(2)无向图
(3)连通图
任意两个顶点之间都有一个路径相连。
- 强连通:有方向的情况下都连通
- 弱连通:不考虑方向的连通
(4)完全图
- 在无向图中,若每对顶点之间都有一条边相连,则为完全图。
- 在有向图中,若每对顶点之间都有两条有向连互连,则为完全图。
n个顶点的无向图和有向图的完全图边的个数计算:
- 无向图:n ∗ ( n − 1 ) 2 \frac{n*(n-1)}数据结构和算法2n∗(n−1)
- 有向图: n ∗ ( n − 1 ) n*(n-1)n∗(n−1)
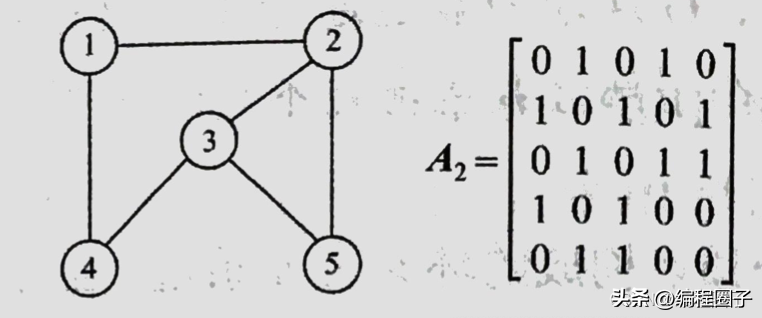
2. 图的转换:无向图转邻接矩阵
用一个n阶的方阵R来存放图中各结点的关联信息。
无向图转换的邻接矩阵为对称矩阵。
有向图转邻接矩阵
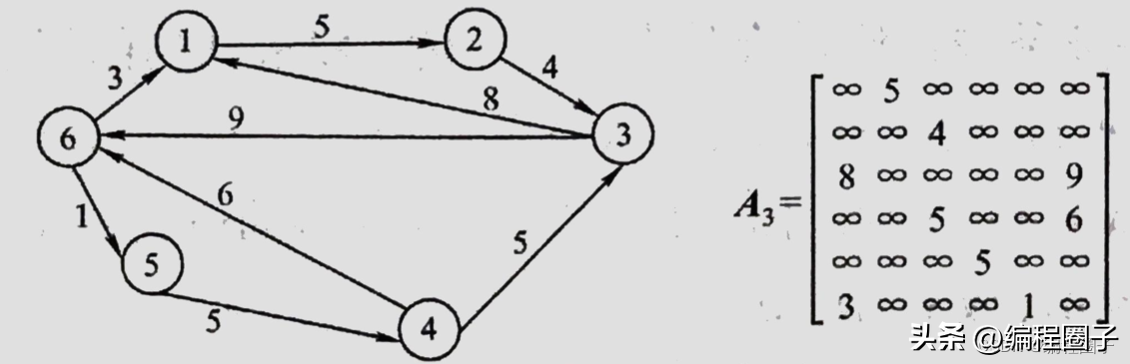
无穷大表示无连接。
3. 度
(1)入度
指向该结点的边的数量
(2)出度
从该结点指出去的边的数量。
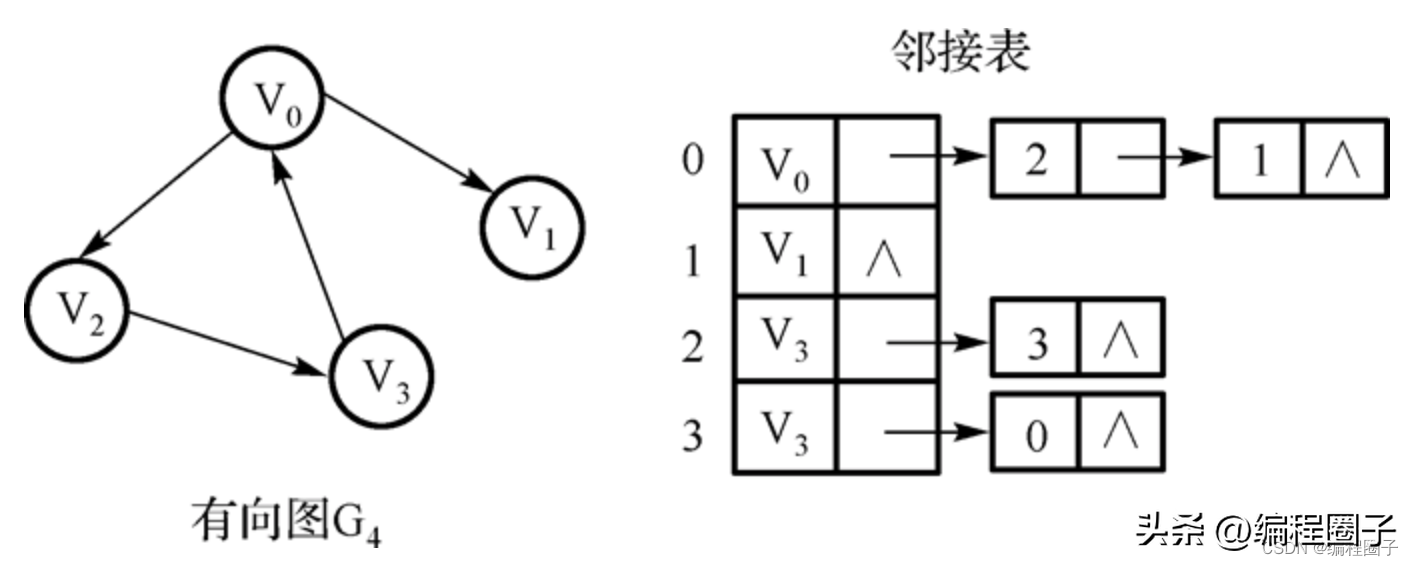
4. 有向图转邻接链表
六、算法特性与复杂度
1. 算法的特性
- 有穷性
- 确定性
2. 算法评价指标
- 正确性
- 友好性
- 可读性
- 健壮性
- 效率
3. 时间复杂度
常见的算法时间复杂度:
O ( 1 ) < ( l o g 2 n ) < O ( n ) < O ( n l o g 2 n ) < O ( n 2 ) < O ( n 3 ) < O ( 2 n ) O(1) < (log_2n) <O(n) <O(nlog_2n) <O(n^2)<O(n^3)<O(2^n) O(1)<(log2n)<O(n)<O(nlog2n)<O(n2)<O(n3)<O(2n)
- 二分查找: l o g 2 n log_2nlog2n
- 一次循环: O(n)
- 插入、冒泡、选择排序:O ( n 2 ) O(n^2)O(n2)
4. 空间复杂度
临时空间占用大小。
七、查找
1. 顺序查找
从头到尾依次查找。
平均查找长度: n + 1 2 \frac{n+1}数据结构和算法2n+1
2. 二分查找(折半查找)
- 前提:有序表、顺序表。
- 折半出现小数时向下取整。
- 折半查找的时间复杂度为O ( l o g 2 n ) O(log_2n)O(log2n)
- 折半查找成功时关键字的比较次数最多为l o g 2 n + 1 log_2n+1log2n+1次。
(1)二分法查找循环算法
int biSearch(int r[], int low, int high, int key){ int mid; while(low<=high ){ mid = (low+high)/2; if(key == r[mid]) return mid; else if(key<r[mid]) high = mid-1; else low = mid+1; } return -1;}int main(){ int data[] = {1,2,3,4,5}; int low=0; int high=sizeof(data) /sizeof(int); int key=3; int find = biSearch(data, low, high, key); printf("result: %d", find);}(2)二分法排序递归算法
int biSearchRecursion(const int r[], int low, int high, int key){ int mid; if(low<=high){ mid = (low + high) /2; if(key ==r[mid]) return mid; else if(key<r[mid]) return biSearchRecursion(r, low, mid-1, key); else return biSearchRecursion(r, mid+1, high, key); } return -1;}int main(){ const int data[] = {1,2,3,4,5}; int low=0; int high=sizeof(data) /sizeof(int); int key=3; int find = biSearchRecursion(data, low, high, key); printf("result: %d", find); return 0;}3. 散列表查找:
(1)线性探查法
- 示例散列函数: h = k e y h=key%7h=key
- 冲突解决:放在后面最近的空格里
(2)拉链法
仍使用散列函数,用链地址法。按关键码构造链,链的数量与关键码一致。
八、排序
1. 基本概念
- 稳定排序:相同值排序后保持前后序号
- 不稳定排序:相同值排序后序号不保持原来顺序
2. 插入类排序
(1) 直接插入排序
插入的元素与现有元素挨个比较,每次从元素前面一个元素比较,比前一元素小的话就继续往前比较。
直接插入排序在元素基本有序时比较有优势。
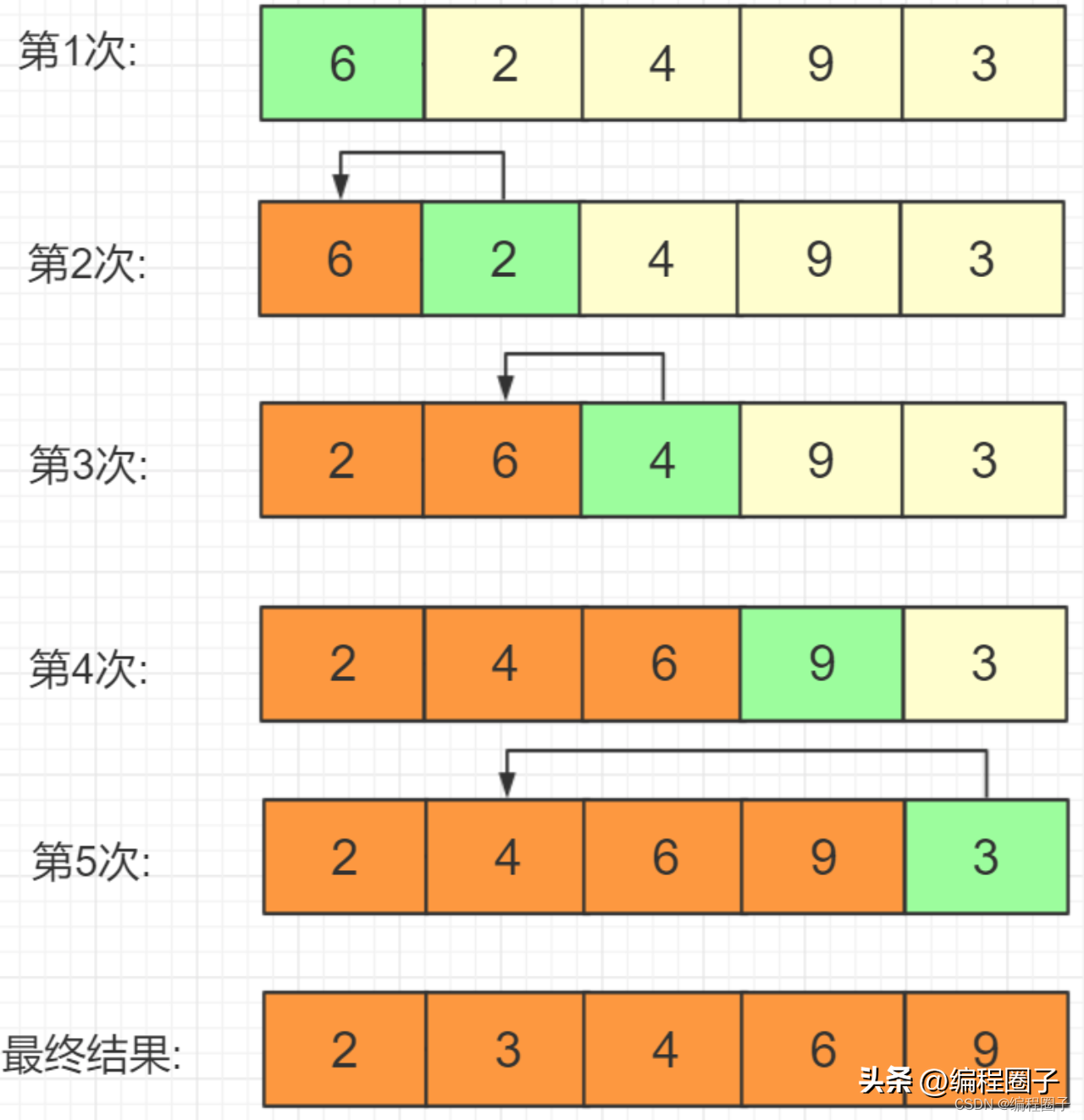
代码示例:
void insertSort(int data[], int n){ int i,j; int tmp; for(i=1;i<n;i++){ if(data[i]<data[i-1]){ tmp = data[i]; data[i] = data[i-1]; // 元素往后移 for(j=i-2;j>=0 && data[j]>tmp;j--){ data[j+1]=data[j]; } data[j+1]=tmp; } }}int main(){ int data[] = {3,4,5,3,5,1,22}; insertSort(data, 7); for(int i=0;i<7;i++){ printf("%d=%d\n", i, data[i]); } return 0;}(2)希尔排序
不稳定排序
3. 交换类排序
(1)冒泡排序
相邻元素比较和交换,一趟排序后最大移到最右、或最小移到最左。
示例代码:
#include <stdio.h>int less(int x,int y){ return ((x<y)?1:0);}int large(int x, int y){ return ((x>y)?1:0);}void bubbleSort(int arr[], int n, int(*compare)(int,int)){ int i,j; int swapped =1; for(i=0;swapped;i++){ swapped=0; for(j=0;j<n-1;j++){ if(compare(arr[j+1],arr[j])){ swap(arr[j+1], arr[j]); swapped = 1; } } }}void bubbleSortTest(){ int data1[] = {4,2,6,3,1}; bubbleSort(data1, 5, less); for(int i : data1){ printf("%d ", i); }}int main() { bubbleSortTest(); return 0;}(2)快速排序
代码:
int qusort(int s[],int start,int end) //自定义函数 qusort(){ int i,j; //定义变量为基本整型 i=start; //将每组首个元素赋给i j = end; //将每组末尾元素赋给j s[0]=s[start]; //设置基准值 while(i<j) { while(i<j&&s[0]<s[j]) j--; //位置左移 if(i<j) { s[i]=s[j]; //将s[j]放到s[i]的位置上 i++; //位置右移 } while(i<j&&s[i]<=s[0]) i++; //位置左移 if(i<j) { s[j]=s[i]; //将大于基准值的s[j]放到s[i]位置 j--; //位置左移 } } s[i]=s[0]; //将基准值放入指定位置 if (start<i) qusort(s,start,j-1); //对分割出的部分递归调用qusort()函数 if (i<end) qusort(s,j+1,end); return 0;}4. 选择类排序
(1)直接选择排序
void selectSort(int data[], int n){ // k 指向最小值的下标 int i,j,k; int temp; for(i=0;i<n-1;i++){ for(k=i,j=i+1;j<n;j++){ if(data[j]<data[k])k=j; if(k!=i){ temp = data[i]; data[i]=data[k]; data[k]=temp; } } }}(2) 堆排序
- 大顶堆:越往上越大,父亲节点大于孩子结点;
- 小顶堆:越往下越大,孩子结点大于父亲结点;
5. 归并排序
6. 基数排序
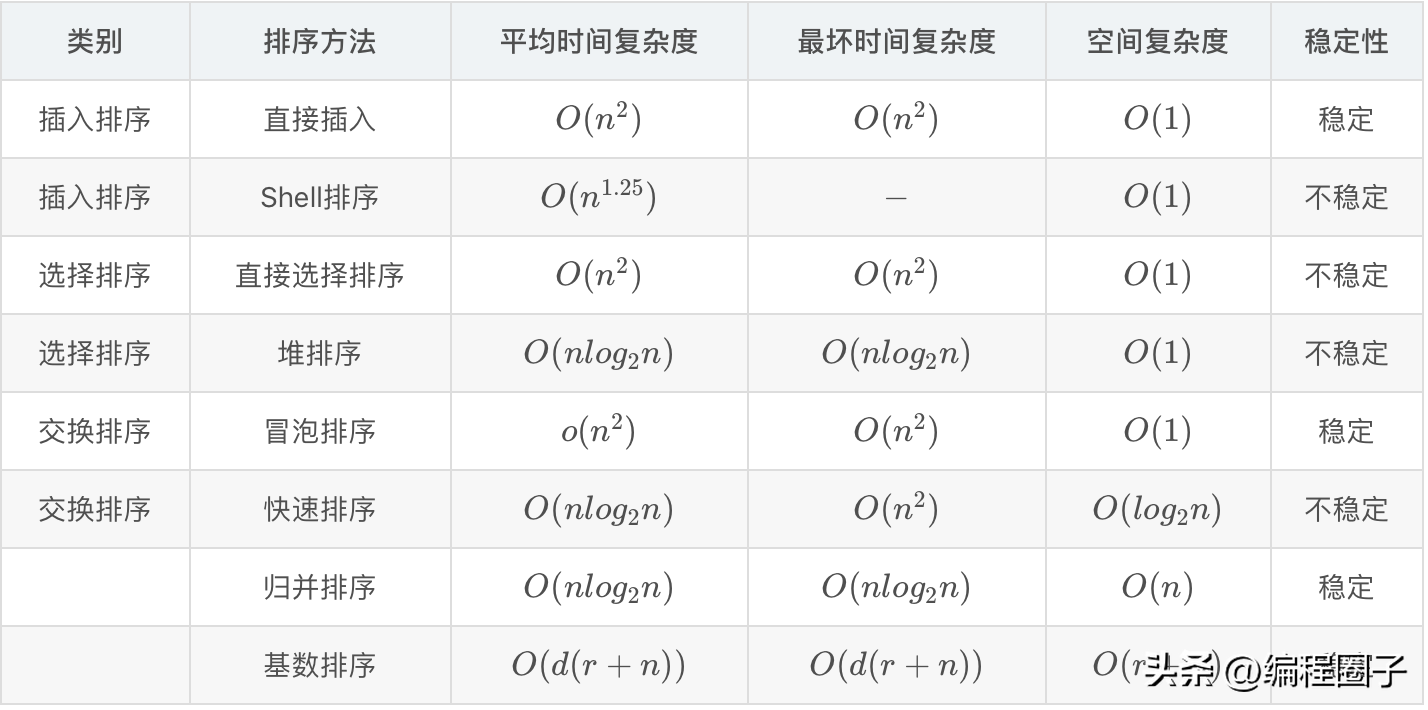
7. 总结
 鲁公网安备37020202000738号
鲁公网安备37020202000738号