C++编程高手接受「十亿行挑战」，速度提升惊人！

“十亿行挑战”是对 Java 开发者的一项挑战，目标是要在最快时间内处理 10 亿行数据。虽然最初这个挑战是针对 Java 的，但本次挑战是展示 C++ 代码优化和相关性能工具的绝佳机会。（本文涉及的完整源代码地址：
https://github.com/HappyCerberus/1brc。）

挑战内容

我们的输入是一个名为 measurements.txt 的文件，其中包含来自不同测量站的温度测量数据。该文件包含十亿行数据，格式如下：

station name;valuestation name;value

测量站名称是一个最多 100 字节的 UTF-8 字符串，包含任何 1 字节或 2 字节的字符（但不能包含‘;’或‘\n’），测量值介于 -99.9 到 99.9 之间，均保留一位小数。另外，唯一键的总数最多为 10,000 个。

输出是一个按字母顺序排序的测量站列表，每个站点都有测得的最低温度、平均温度和最高温度。

{Abha=-23.0/18.0/59.2, Abidjan=-16.2/26.0/67.3, Abéché=-10.0/29.4/69.0, ...}

最初实现

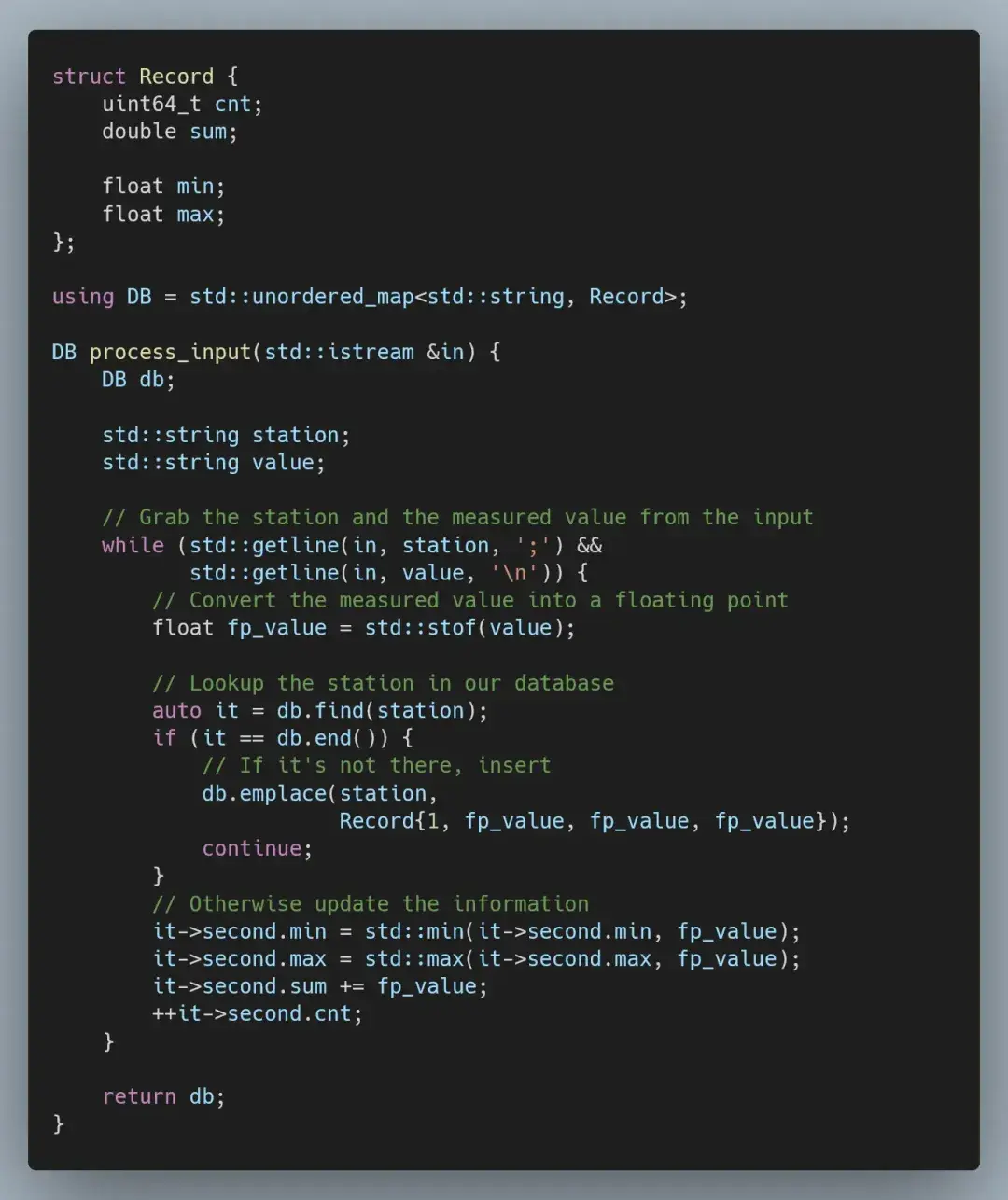
当然，我们首先要从基准实现开始。我们的程序将分为两个阶段：处理输入和格式化输出。对于输入部分，我们解析测量站名称和测量值，并将它们存储在一个 std::unordered_map 中。

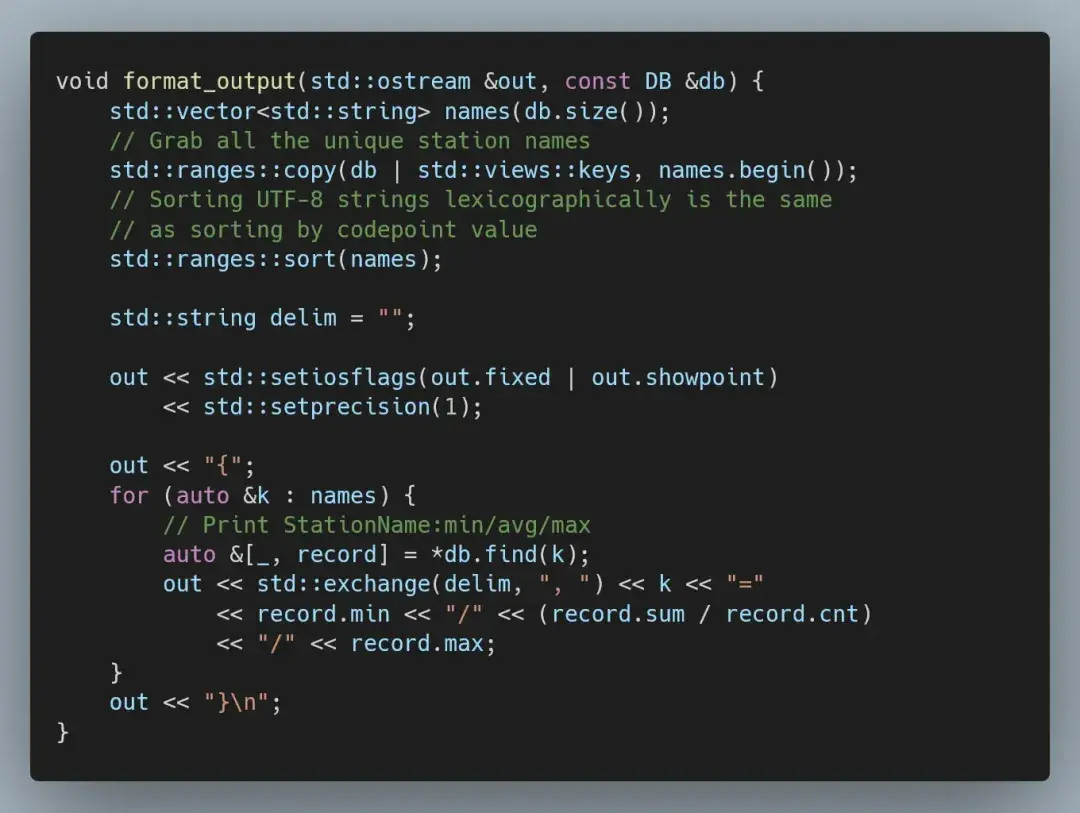
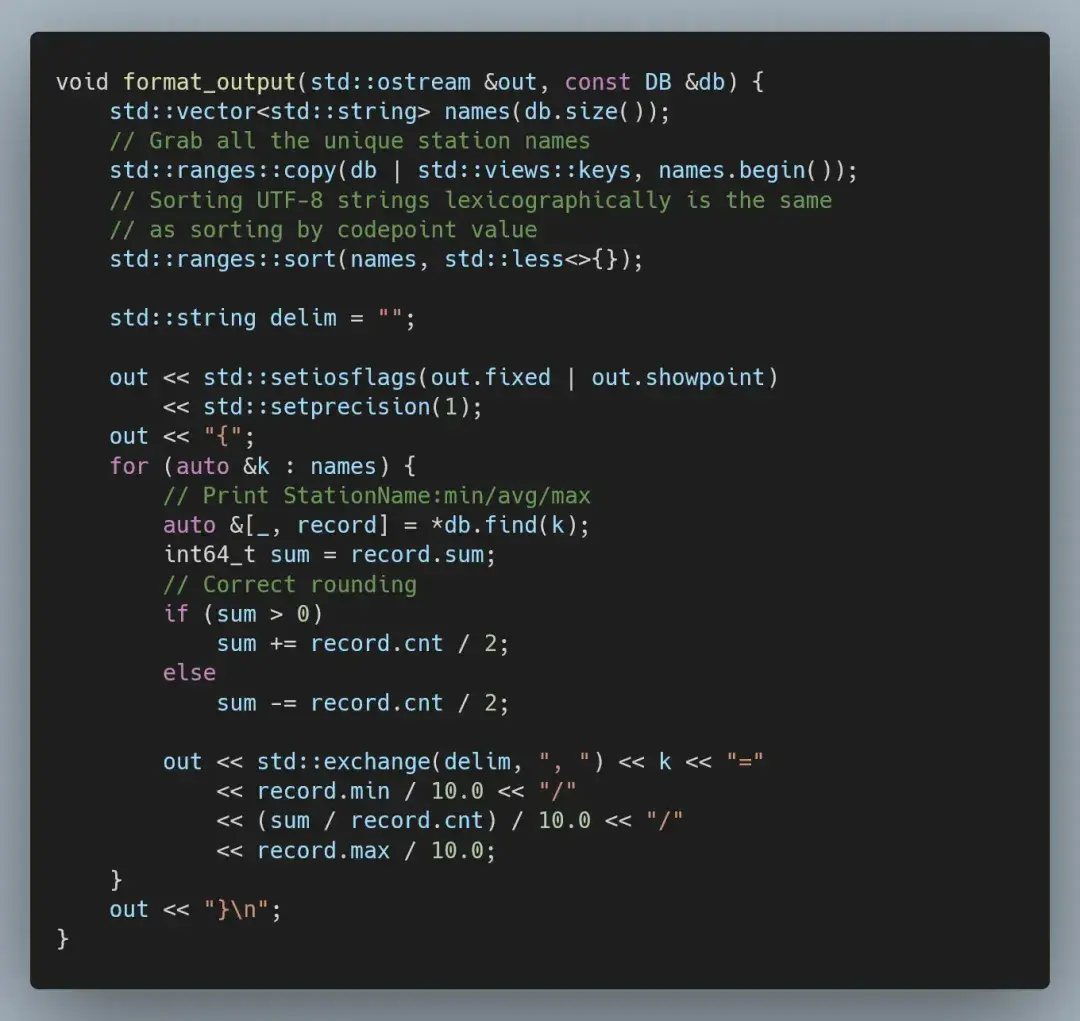
为了生成输出结果，我们整理了唯一名称并按字母顺序对其进行排序，然后打印出最低、平均和最高测量值。

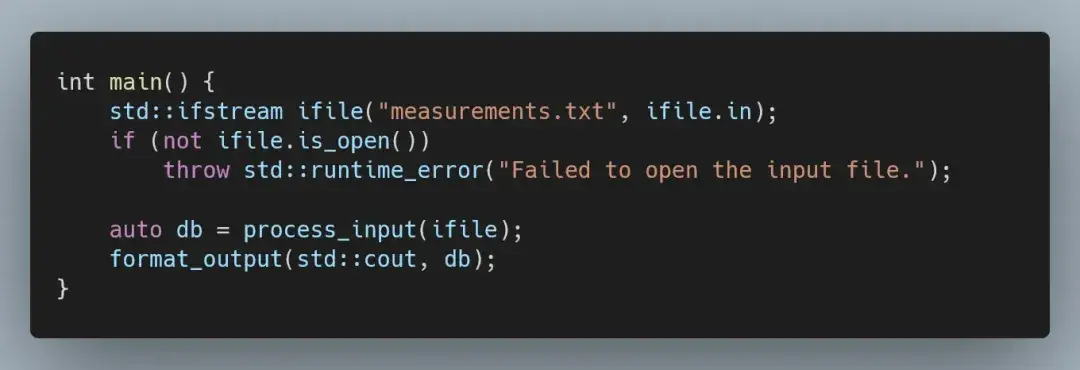
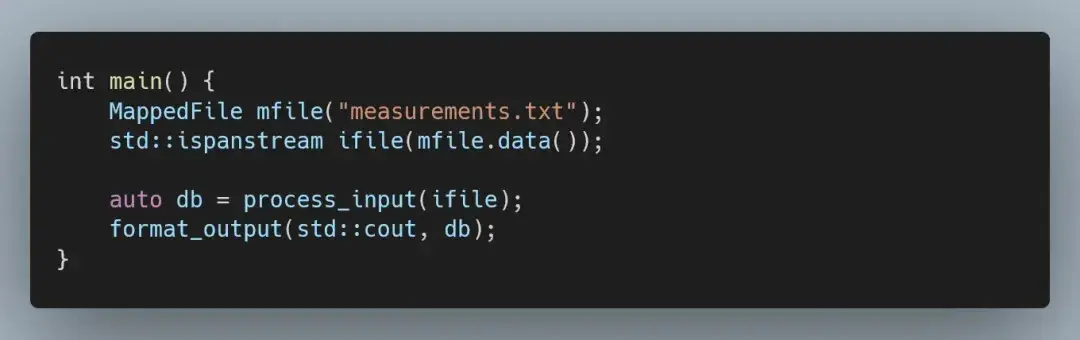
只剩下一个简单明了的主函数，将这两个部分连接在一起。

这个实现非常简单，但它有两个主要问题：一是不正确（暂时先不管），二是速度非常慢。为此，我们在以下三台设备上跟踪性能：

● Fedora 39 上的 Intel 9700K

● Windows Subsystem for Linux（WSL）上的 Intel 14900K

● Mac Mini M1（8 核）

在 9700K 上用 clang 17 编译二进制文件，在 14900K 上用 clang 18 编译二进制文件，在 Mac Mini 上用 Apple clang 15 编译二进制文件。这三台设备都用了相同的编译标志：

-O3 -march=native -g0 -DNDEBUG -fomit-frame-pointer

由于我们主要关注的是相对性能的提升，因此测量结果仅为相应设备上的最快运行时间。

● 9700K（Fedora 39）：132 秒

● 14900K（WSL Ubuntu）：67 秒

● Mac Mini M1：113 秒

消除拷贝

对于第一步优化，我们并不需要特殊工具：高性能代码最重要的原则就是避免过多拷贝，而我们却无意间进行了大量拷贝。

当我们处理一行数据时（记住，共有 10 亿行数据），会将测量站名称和测量值读入 std::string 中。这本质上就产生了数据拷贝，因为当我们从文件中读取数据时，文件内容已经在内存中的缓冲区了。

为了消除这个问题，我们有几个选择：改用非缓冲读取，手动处理 istream 的缓冲区；用更系统级的方法，例如对文件进行内存映射——在本文中，我们将采取后者。

当我们将文件进行内存映射时，操作系统会为文件内容分配地址空间，而数据仅在需要时才会读入内存。这样做的好处是，我们可以将整个文件视为一个数组；缺点是，我们无法控制当前内存中文件的哪些部分是可用的。

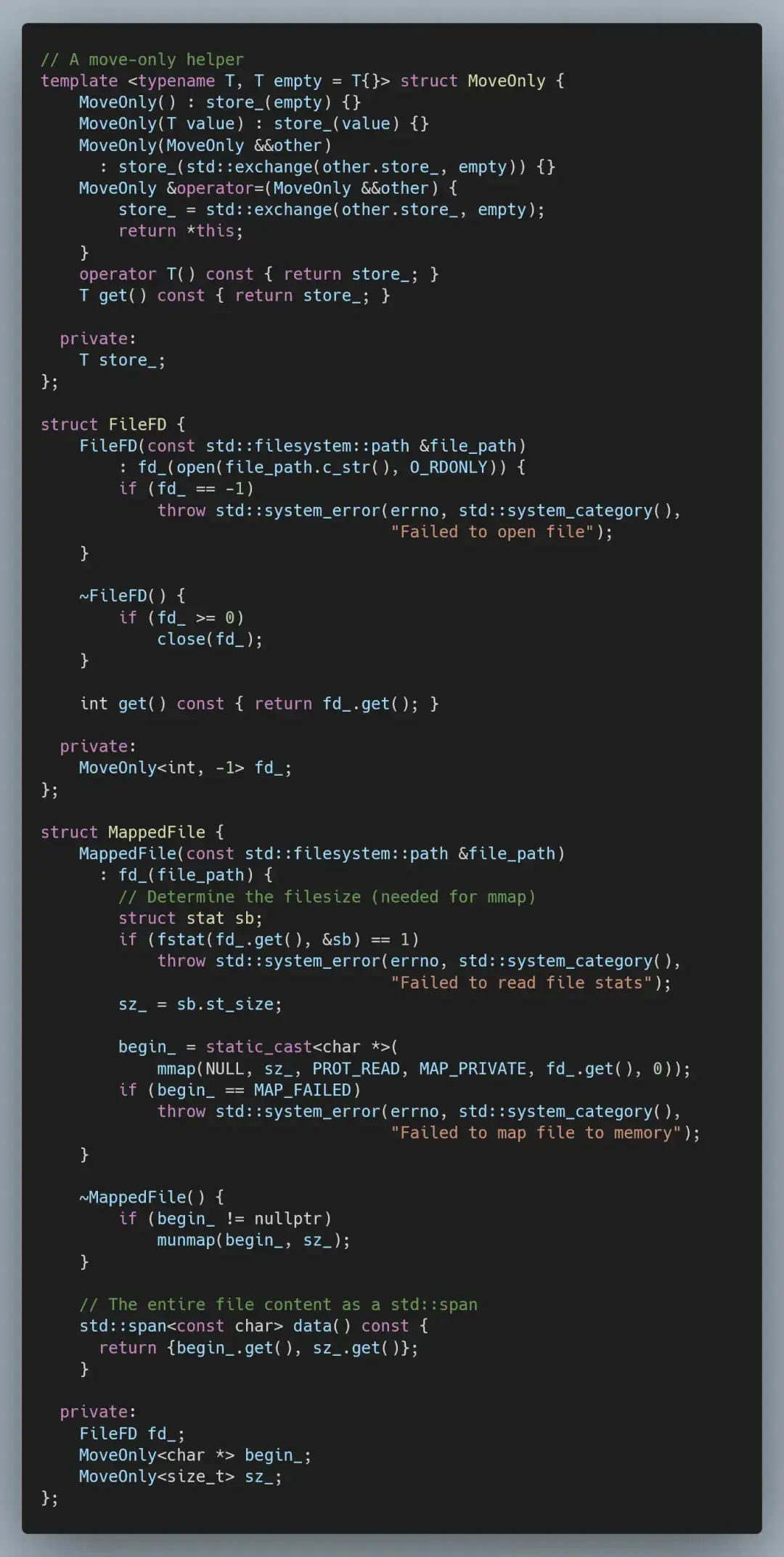
既然我们用的是 C++，那么就用 RAII 对象来封装底层系统逻辑吧。

因为我们将内存映射文件封装在 std::span 中，因此只需将 std::ifstream 换成 std::ispanstream 就能验证一切是否正常。

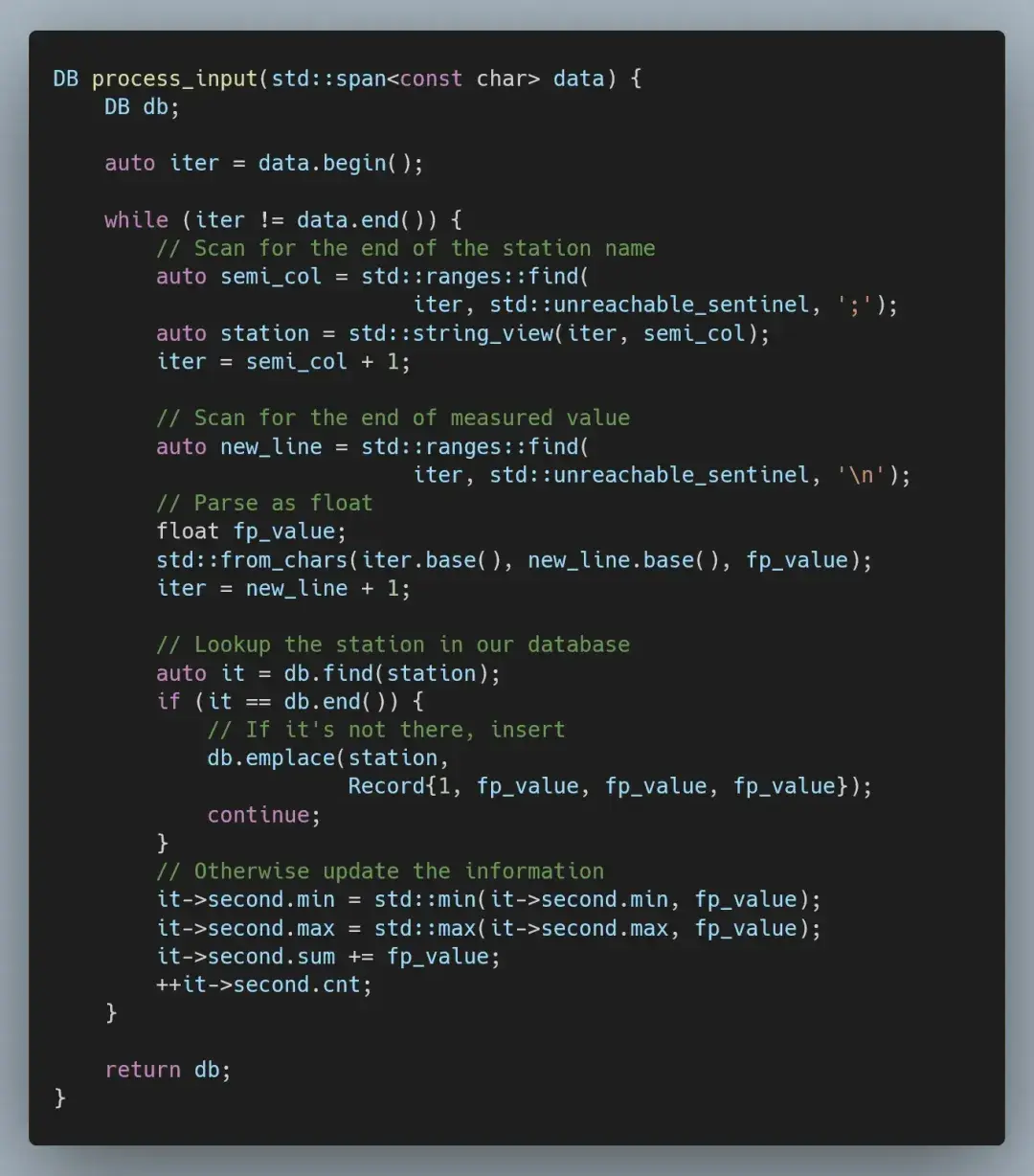
不过，虽然这可以确保一切正常，但并不能消除任何过多的拷贝。为此，我们必须将输入处理从在 istream 上操作切换为将输入视为一个大 C 风格字符串。

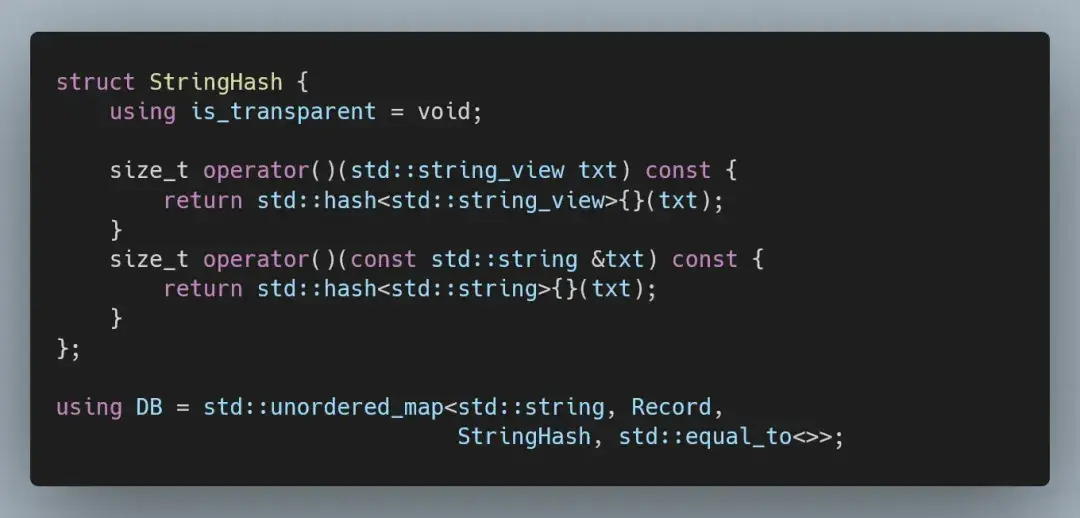
我们需要调整哈希映射以支持异构查找，因为现在用 std::string_view 查找测量站，这会涉及更改比较器和添加自定义哈希函数。

这一优化使我们的解决方案运行速度大幅提高（暂时跳过 M1，因为 clang 15 不支持浮点类型的std::from_chars）。

● 9700K（Fedora 39）：47.6 秒（2.8 倍）

● 14900K（WSL Ubuntu）：29.4 秒（2.3 倍）

分析情况

为了进一步优化解决方案，我们必须分析哪些部分是主要瓶颈，这就需要一个性能分析工具。

至于分析工具的选择，我们必须在精度和低开销之间做出平衡。在本文中，我们将使用 perf：这是一个 Linux 性能分析工具，开销极低的同时能提供合理精度。

要记录性能分析，我们必须在二进制文件中注入一些调试信息：

-fno-omit-frame-pointer # do not omit the frame pointer-ggdb3 # detailed debugging information

接着在 perf 工具下运行二进制文件：

perf record --call-graph dwarf -F999 ./binary

callgraph 选项允许 perf 利用二进制文件中存储的调试信息，将低级函数归属于正确的调用者。第二个选项会降低 perf 捕捉样本的频率；如果频率过高，可能会丢失一些样本。

然后，我们就可以查看性能分析了：

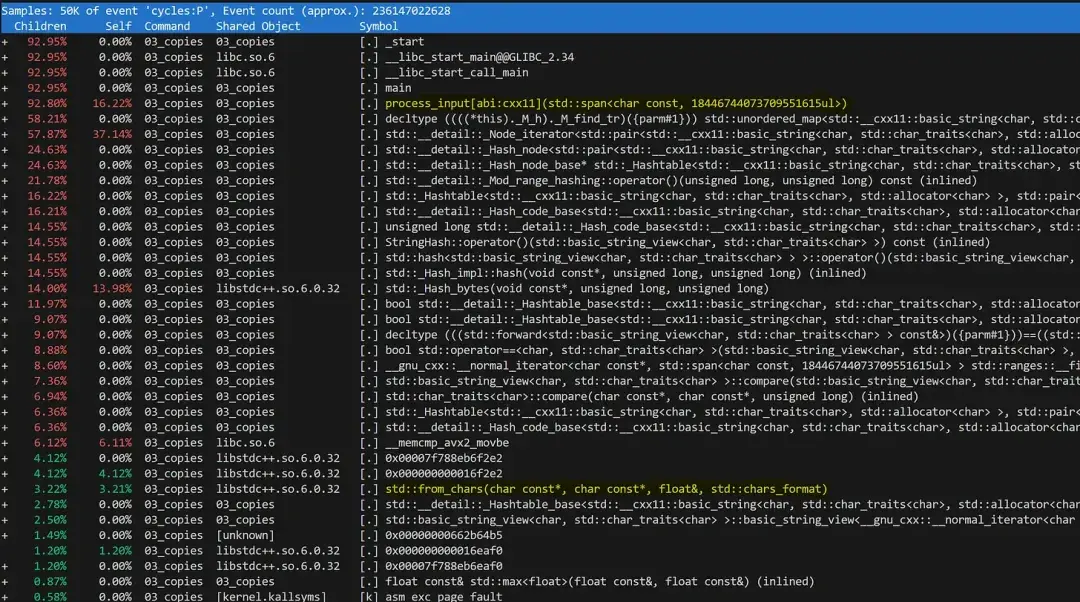
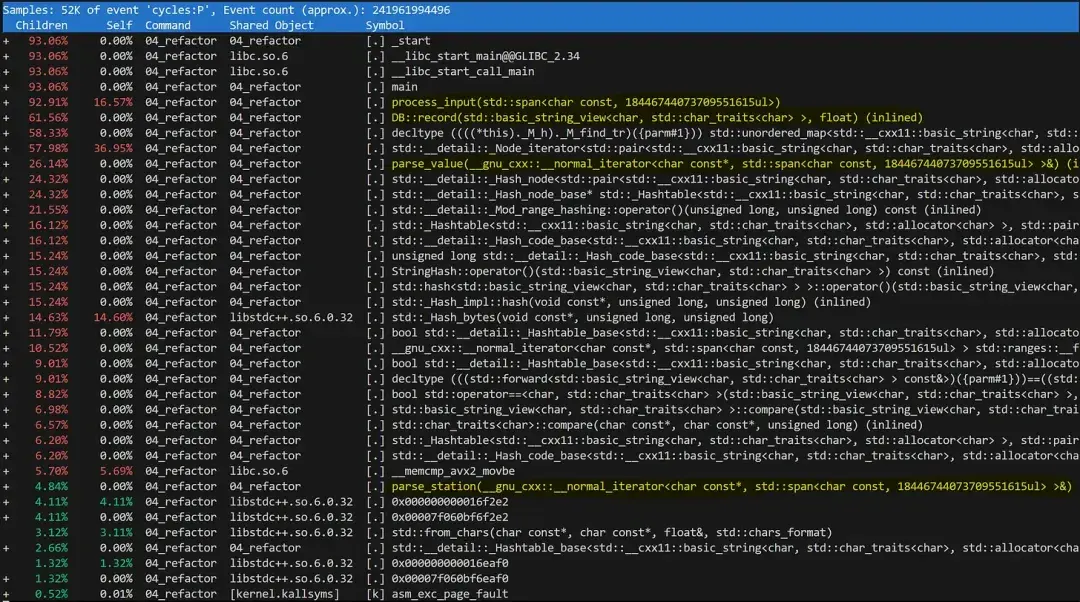
perf report -g 'graph,caller'

不过，如果我们在当前实施方案中运行 perf，只能得到一个信息量较为有限的性能分析。

可以推断出，运行时间的最大部分都花费在 std::unordered_map 中，而其余操作都在低级函数中被淹没了。例如，你可能会得出这样的结论：解析测量值只占 3%（std::from_chars 函数）——但这其实是错的。

由于我们将所有逻辑都放在了一个紧密的循环中，这样的性能分析就很差。虽然这对性能来说有好处，但却完全失去了正在执行的逻辑操作的意义：

● 解析测量站名称；

● 解析测量值；

● 将数据存储到数据库中。

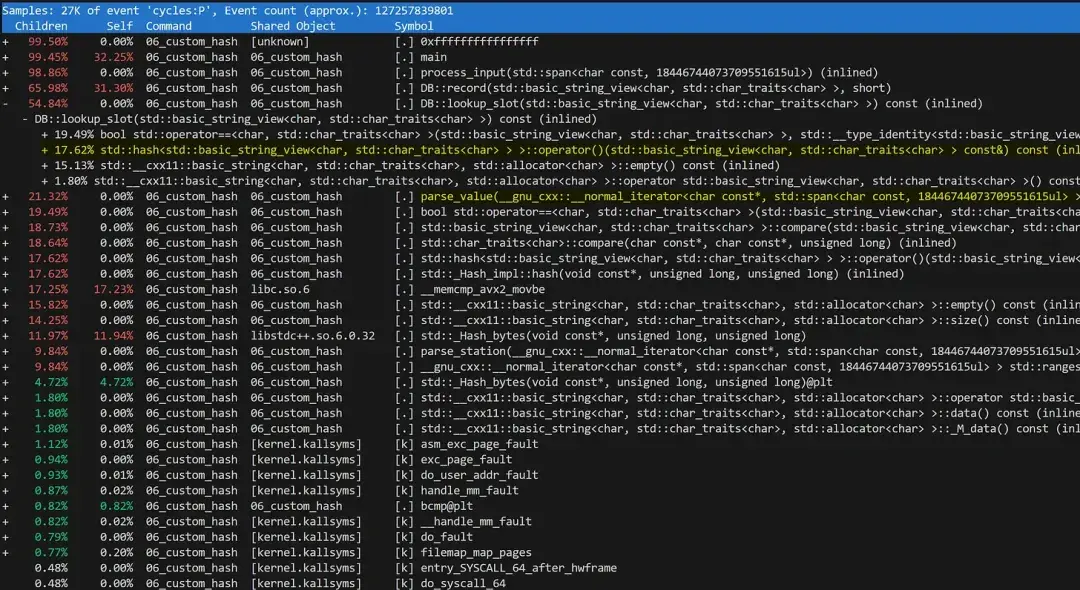
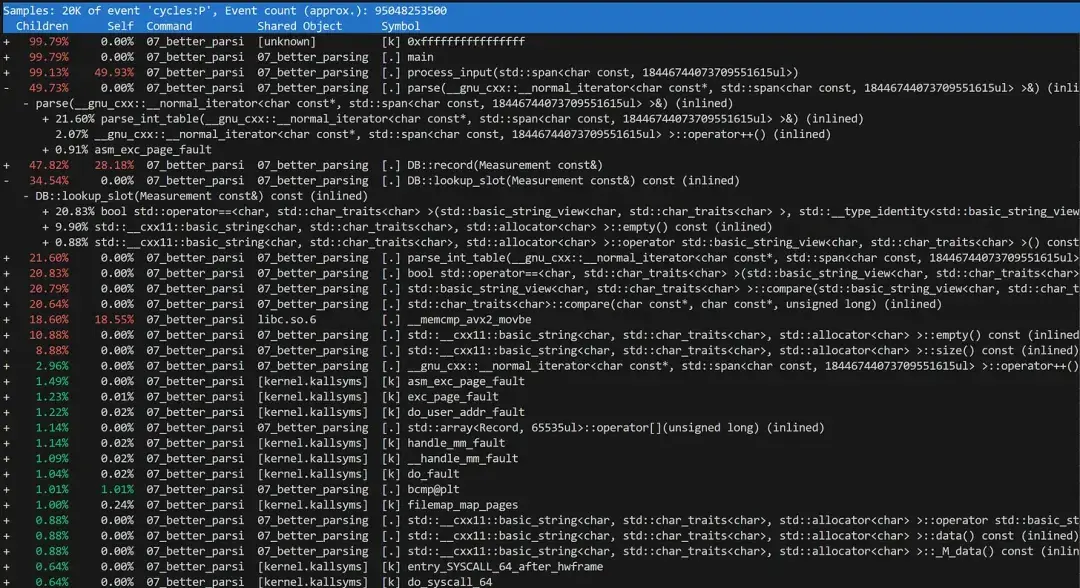
如果我们将这些逻辑操作封装成单独的函数，性能分析的清晰度将大幅提高。

可以看到，我们花费了 62% 的时间将数据插入数据库，26% 的时间解析测量值，以及 5% 的时间解析测量站名称。

接下来应该处理哈希映射，但在此之前，我们先处理一下数值解析问题，这也将修复我们代码中一个长期存在的错误（四舍五入错误）。

虚假的整数

输入包含 -99.9 到 99.9 范围内的测量值，并始终保留一位小数——这意味着，我们首先处理的不是浮点数，因为测量值是定点数。

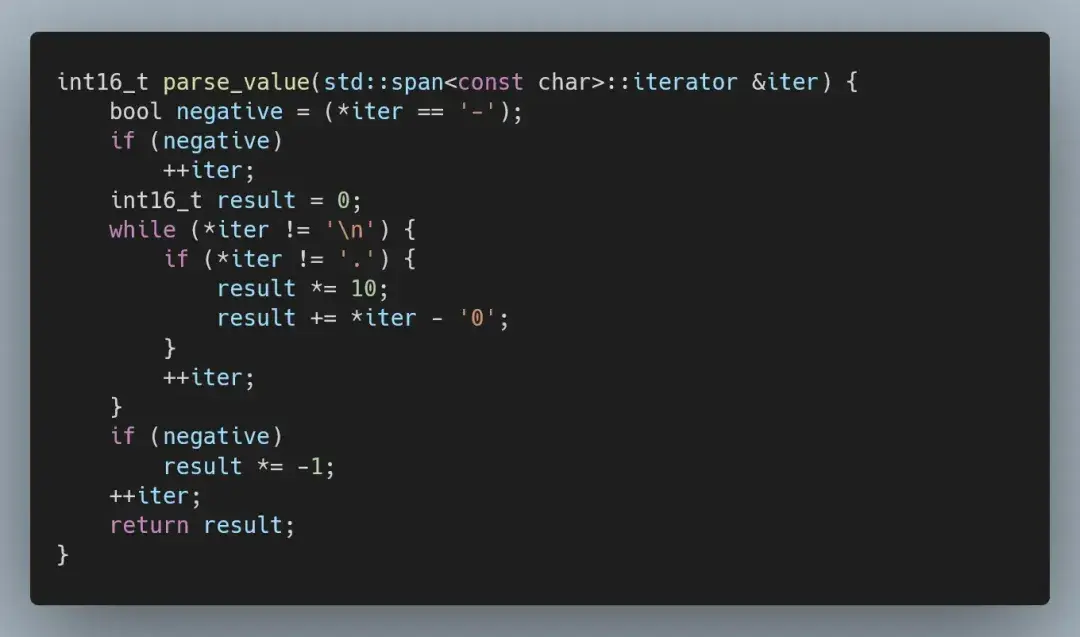
表示定点数值的正确方法，是将其表示为整数，我们可以手动解析（先用直接解析）：

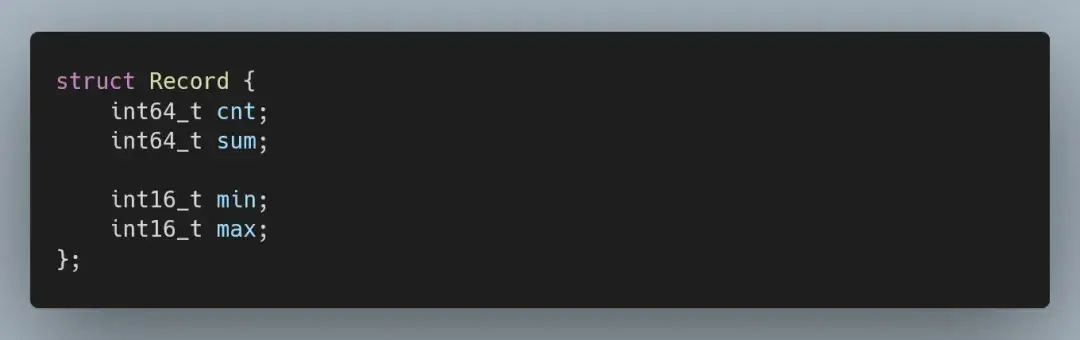
这种变化也会影响到记录的结构：

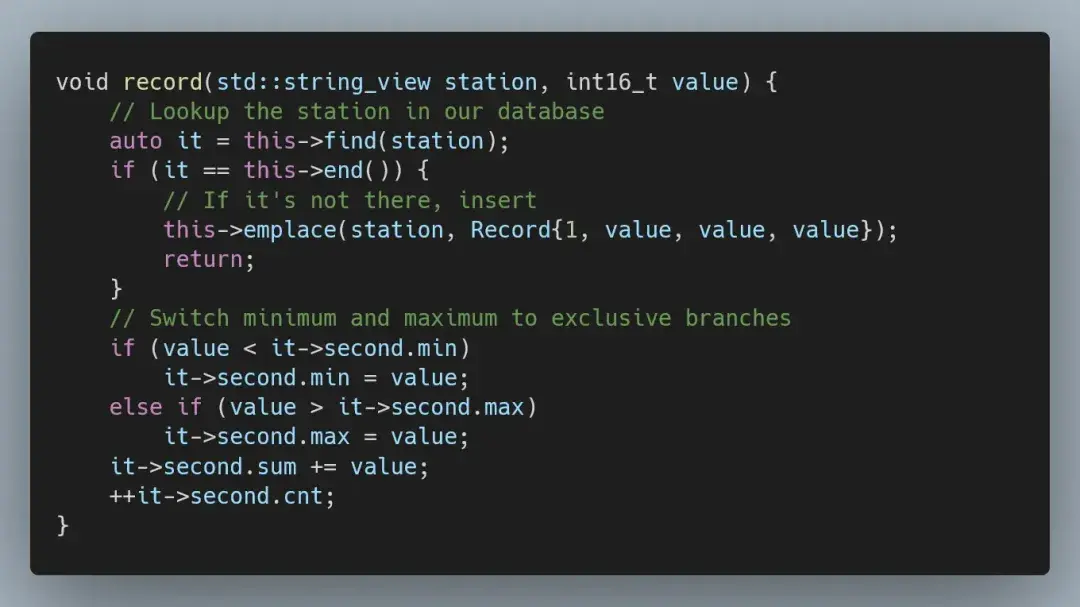
数据库插入可以保持原样，但我们可借此机会稍微优化一下代码。

最后，我们需要修改输出格式的代码。由于现在用的是定点数，所以我们必须将存储的整数值转换并四舍五入成浮点数。

这一优化修复了前面提到的四舍五入错误，并提高了运行时效率（浮点运算速度较慢），且该实现也与 M1 Mac 兼容。

● 9700K (Fedora 39)：35.5 秒（3.7 倍）

● 14900K（WSL Ubuntu）：23.7 秒（2.8 倍）

● Mac Mini M1：55.7 秒（2.0 倍）

自定义哈希映射

标准库中的 std::unordered_map 以速度慢而闻名，这是因为它使用了节点结构（实际上是节点链表数组）。按理说，我们可以改用平面映射（来自 Abseil 或 Boost），但这会违背 1brc 挑战赛的规则——即禁止使用外部库。

更重要的是，我们的输入也非常有限。对于 10 亿条记录，我们只有 1 万个唯一键，因此命中率会极高。

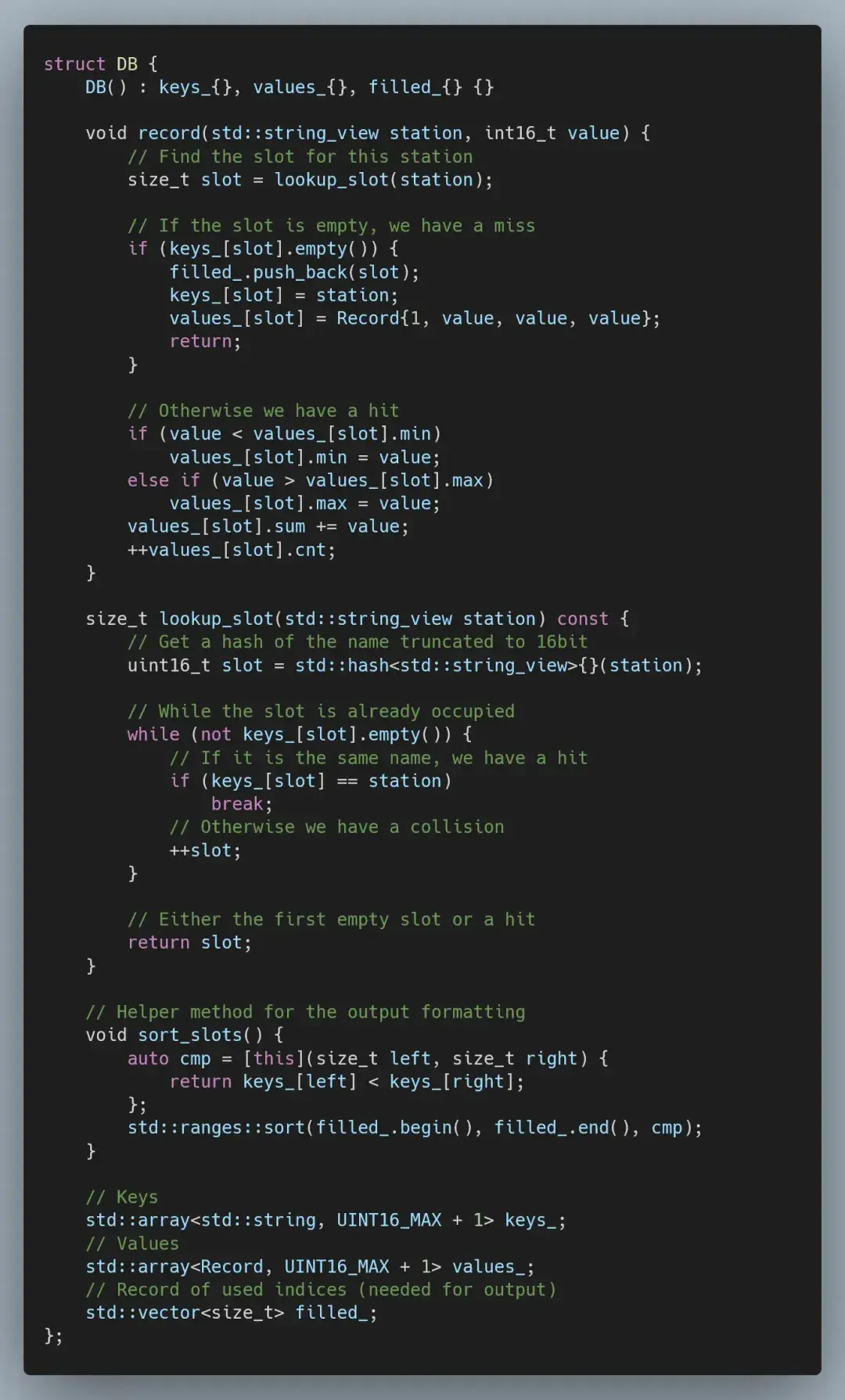
由于我们只能用 1 万个唯一键，因此可用基于 16 位哈希的线性探测哈希映射，直接索引静态数组。当遇到碰撞时（两个不同站点映射到相同的哈希/索引）时，我们将使用下一个可用的槽位。

这就意味着，在最坏的情况下（所有站点都映射到相同的哈希/索引），我们最终会进行线性复杂度查找。然而，这种情况极少发生，对于使用 std::hash 的输入示例，我们最终会遇到 500 万次碰撞，即 0.5%。

这一变动，带来了相当大的速度提升：

● 9700K（Fedora 39）：25.6 秒（5.1 倍）

● 14900K（WSL Ubuntu）：18.4 秒（3.6 倍）

● Mac Mini M1：49.4 秒（2.3 倍）

微调代码

以上，我们已经梳理了高层次的优化途径，接下来是时候深入挖掘并微调代码中的关键部分了。先让我们回顾一下目前的情况。

我们可以在哈希（17%）和整数解析（21%）方面进行一些低级优化。微调代码的正确工具是基准测试框架，我们将实现几个目标函数的版本，并把结果相互比较。在本文中，我们选择使用 Google Benchmark。

（1）解析整数

当前版本的整数解析（故意）写得很差，有过多的分支。

由于数值可以短至三个字符，我们无法有效地利用宽指令（AVX）。在这种情况下，唯一能消除分支的方法就是通过查找表。

当我们解析数字时，只有两种可能的情况（忽略符号）：

● 遇到一个数字：累加器乘以 10 并加上数字值。

● 遇到一个非数字：累加器乘以 1 并加上 0。

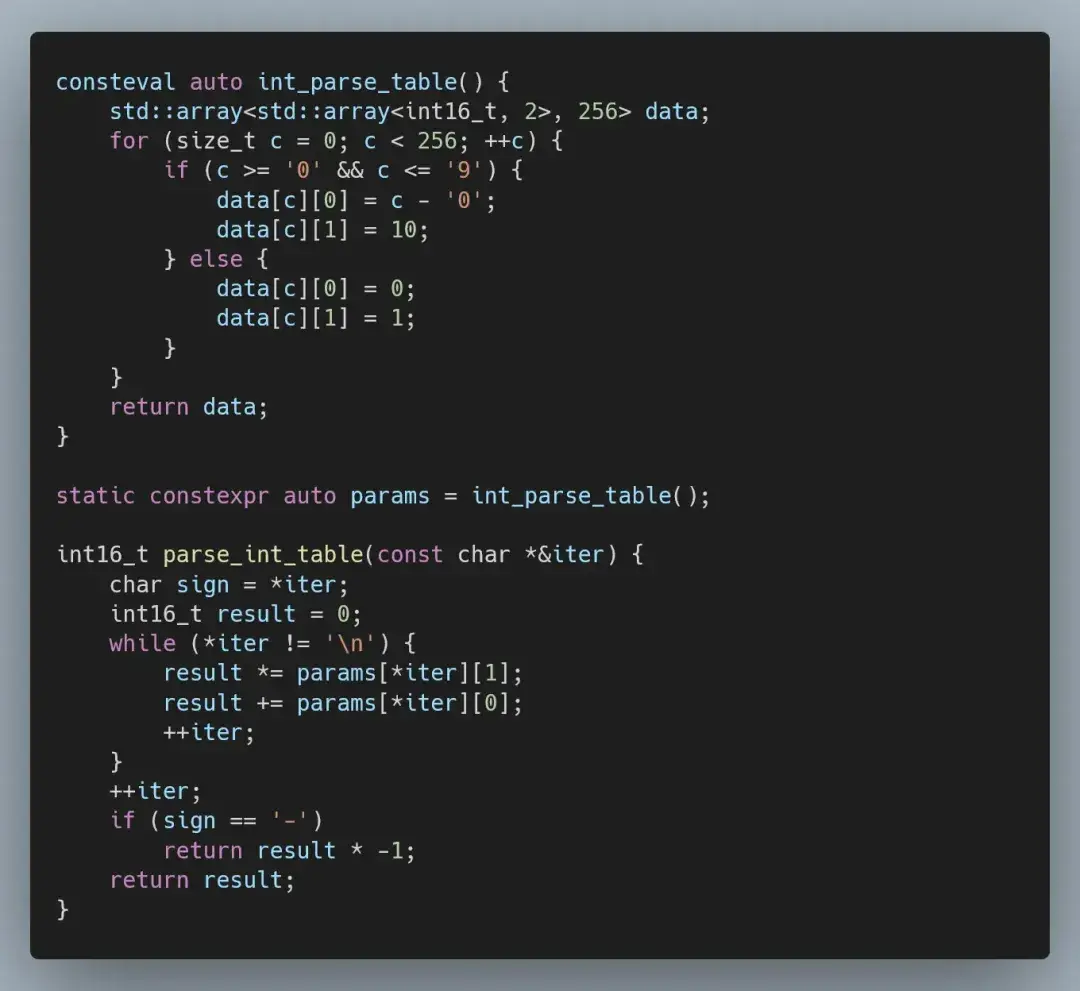
我们可以把这个过程编码为一个二维的、在编译时生成的数组，其中包含 char 类型所有 256 个值的信息。

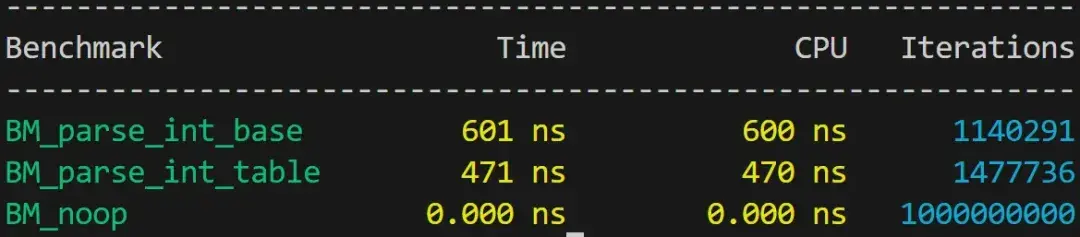
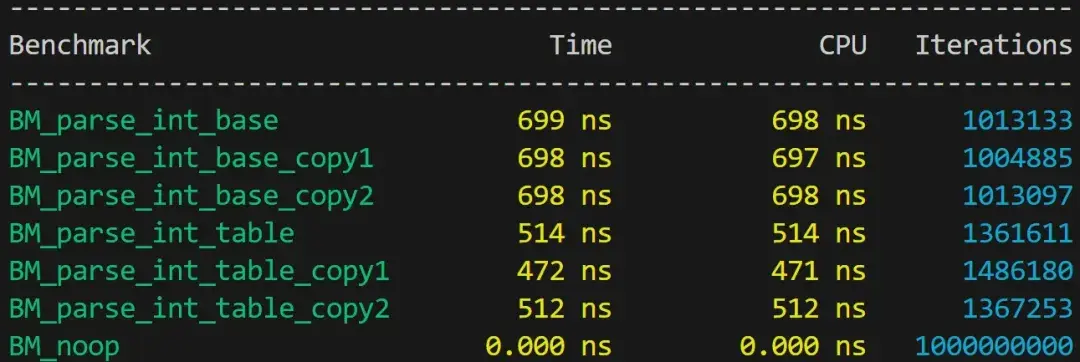
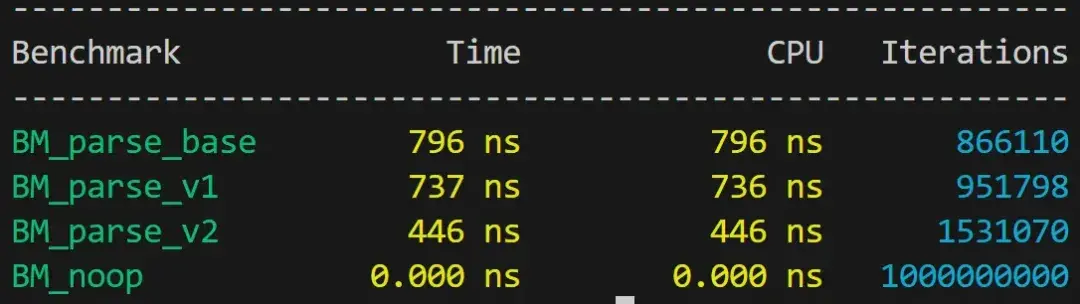
如果我们把这两个版本插入到微基准测试中，就会得到一个非常明确的结果。

但很可惜，我们并不能把这两个版本直接插入到 Google Benchmark 中。我们的实现是一个超过 5 个字符的紧密循环，因此对布局非常敏感，可以用 LLVM 标志来对齐这些函数。

-mllvm -align-all-functions=5

不过即使这样，结果也会有很大波动（高达 40%）。

（2）哈希处理

在进行哈希处理时，我们有两个优化的机会。

目前，我们是先解析站点的名称，然后在 lookup_slot 中计算哈希值，这意味着要对数据进行两次遍历。此外，我们计算的是 64 位的哈希值，但实际上只需要 16 位的哈希值。

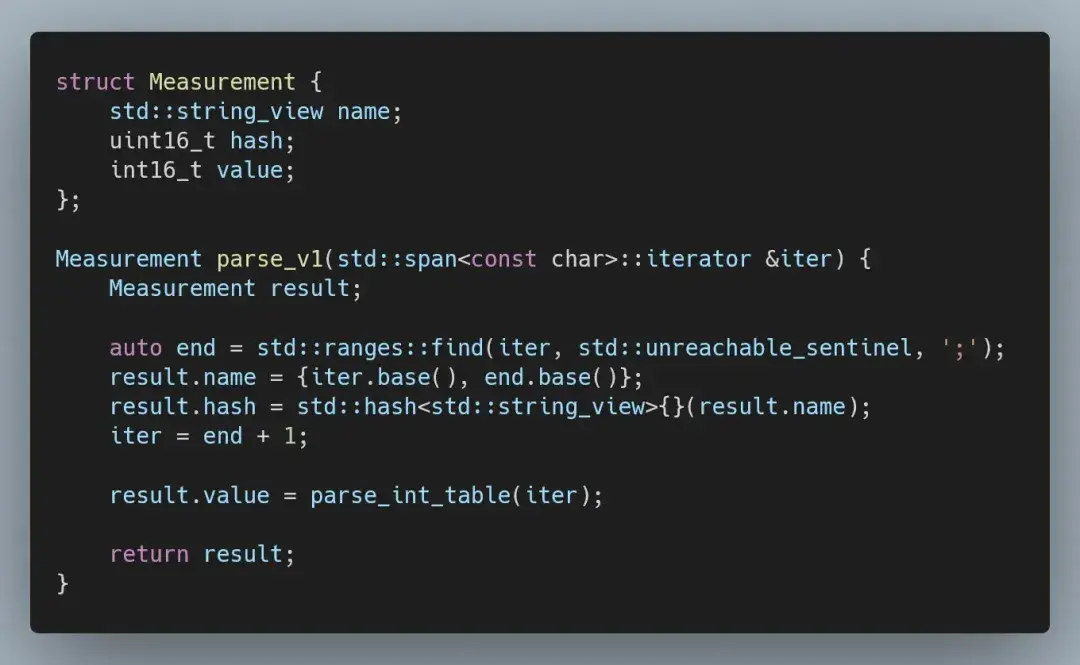
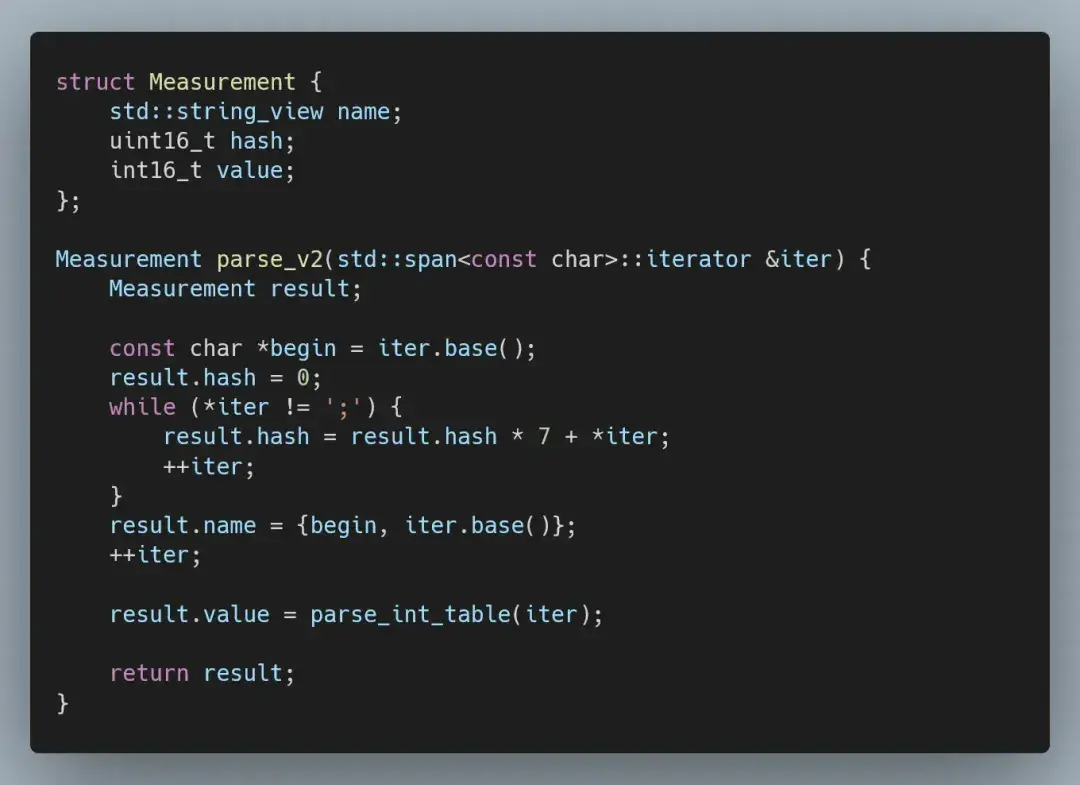
为了减少整数解析时遇到的问题，我们将把解析合并为一个步骤，生成一个站点名称的 string_view、一个 16 位哈希和定点测量值。

我们可以用一个简单公式来计算自定义的 16 位哈希，依赖无符号溢出而不是取模。

这将大幅加快计算速度（同时具有合理的稳定性）。

当我们将这个改进纳入解决方案中后，就会得到整体速度的提升：

● 9700K (Fedora 39)：19.2 秒（6.87 倍）

● 14900K（WSL Ubuntu）：14.1 秒（4.75 倍）

● Mac Mini M1：46.2 秒（2.44 倍速）

释放线程

如果现在研究一下性能分析，就会发现我们已经达到了可行的极限。

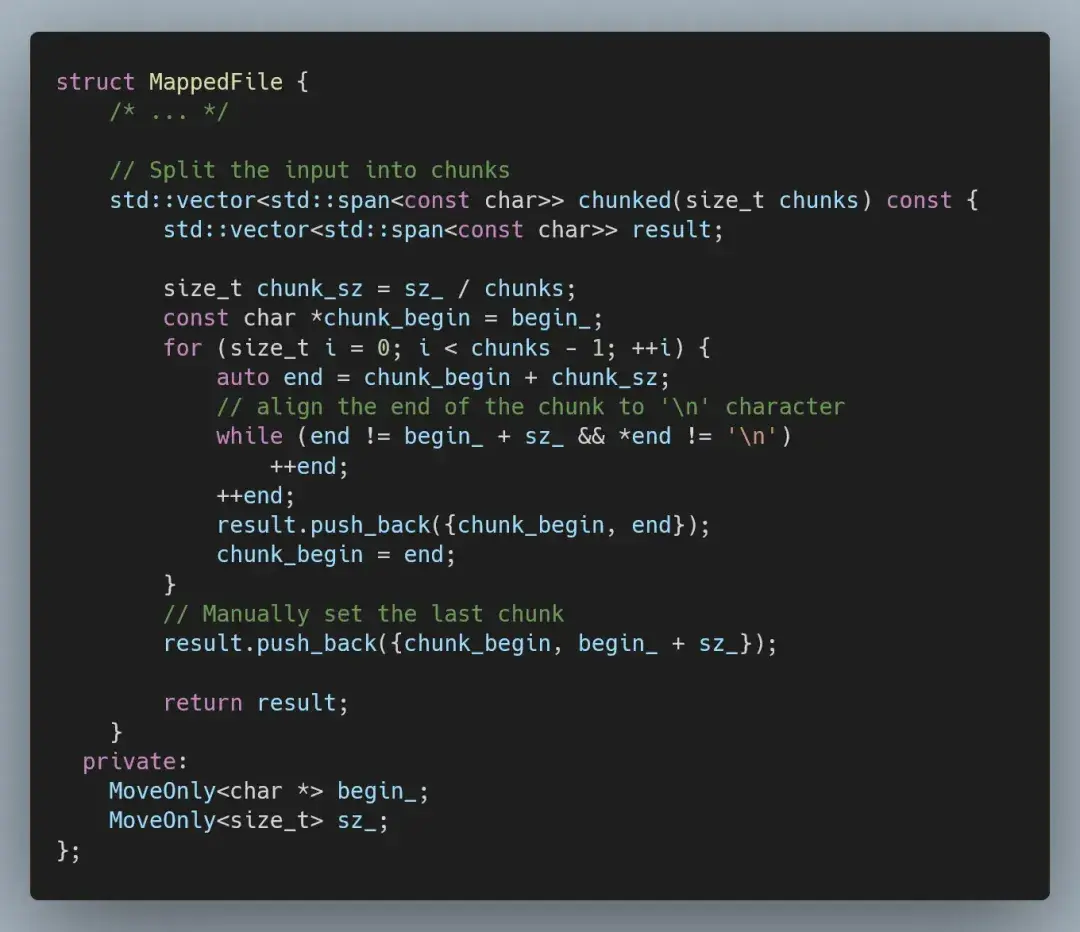
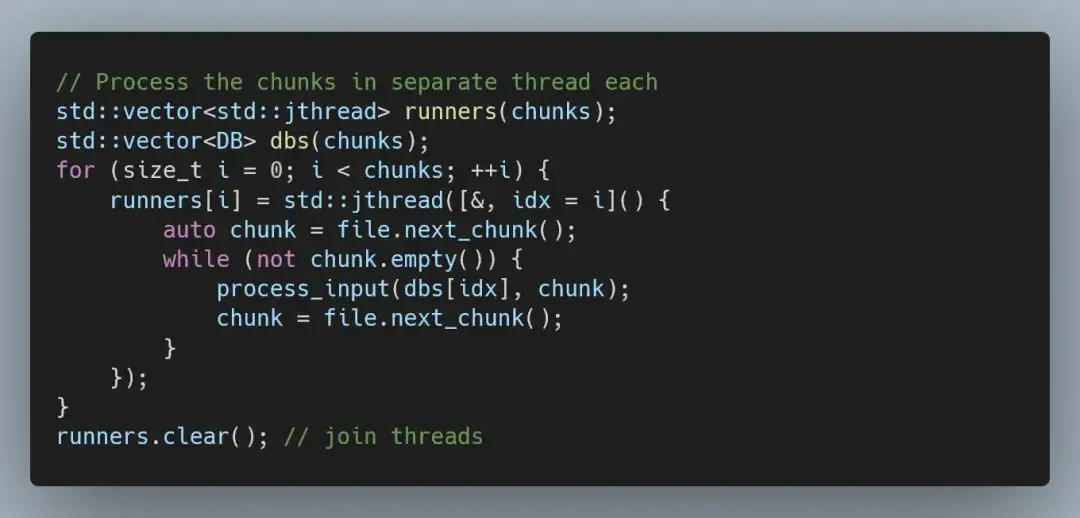
因此，下一步自然是并行化我们的代码。最简单的方法是将输入分成大致相同的块，在单独的线程中处理每个块，然后合并结果。我们可以扩展 MappedFile 类型，以提供分块访问。

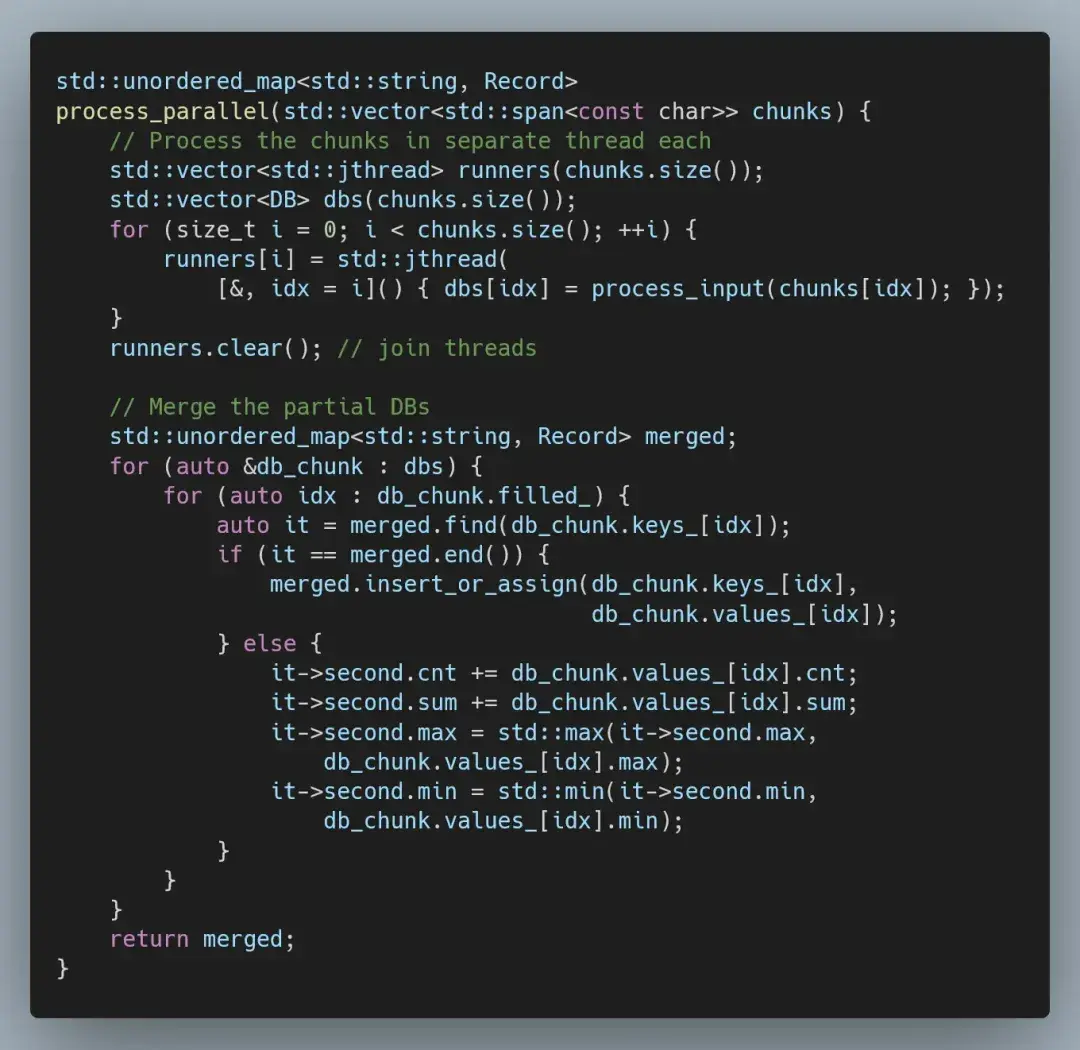
这样，我们就可以简单地在每个线程中按块运行现有代码。

这样的优化效果相当不错。

以下是最佳结果。请注意，这些只是相对比较下的最佳运行结果，而不是严格的基准测试。

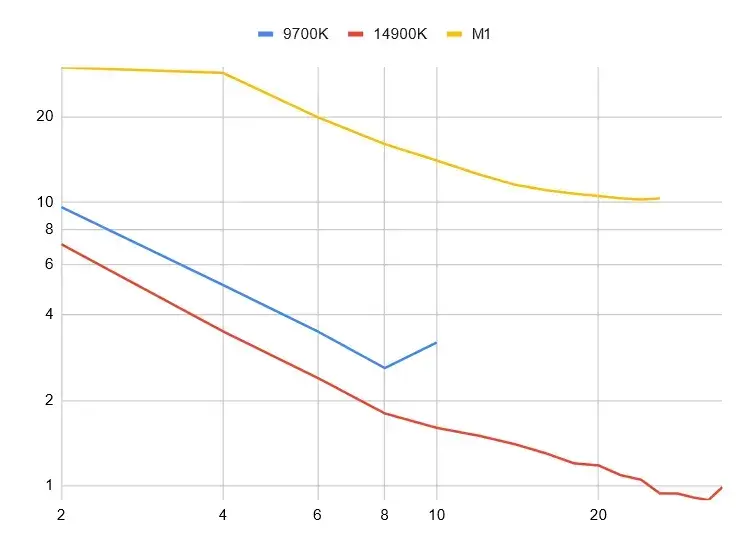
● 9700K（Fedora 39）：2.6 秒（50 倍）（在 8 个线程上）

● 14900K（WSL Ubuntu）：0.89 秒（75 倍）（在 32 个线程上）

● Mac Mini M1：10.2 秒（11 倍）（在 24 个线程上）

（1）处理非对称处理速度

9700K 的缩放非常简洁，但这是因为这款处理器有 8 个不支持超线程的相同内核。一旦我们升级到 14900K，架构中的性能和效率内核就会变得复杂得多。

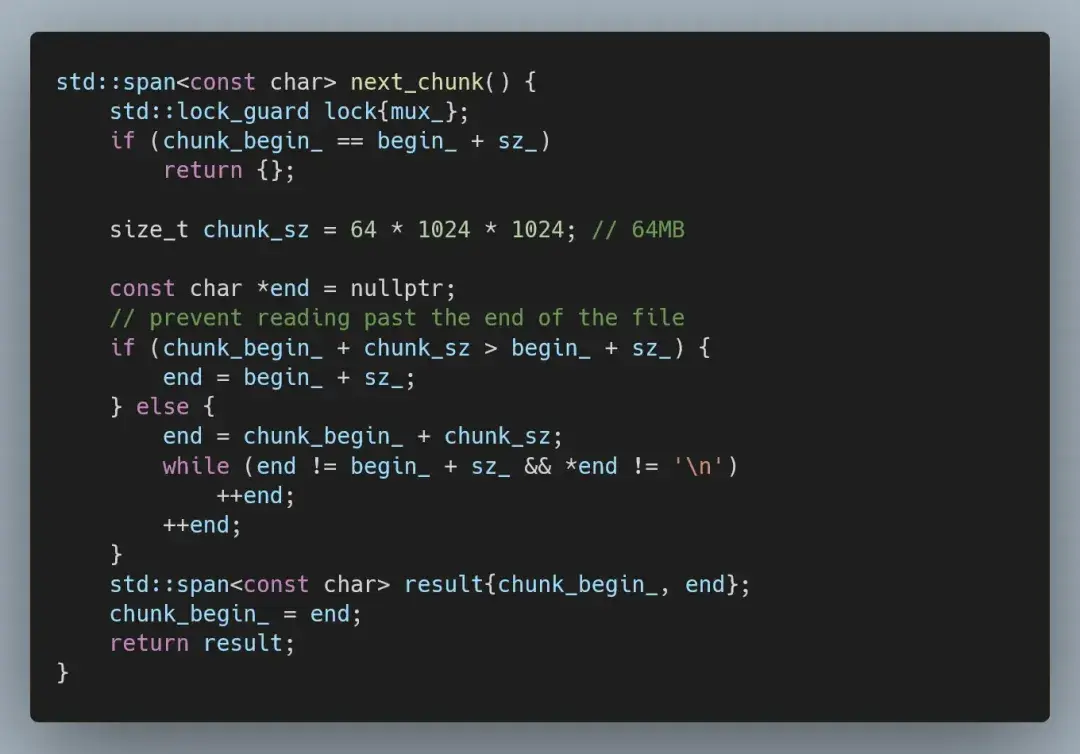
如果我们简单地将输入分成相同的块，效率核心会落后于主核心，拖慢整体运行速度。因此，我们不再将输入分成每个线程一个块，而是让线程按需请求块。

以及 MappedFile 中相应的 next_chunk 方法。

这样我们就可以从 14900K 中挤出最后一丝性能：

● 14900K（WSL Ubuntu）：0.77 秒（87 倍）（在 32 个线程上）

结论

对比最初实现的性能，现在我们已经提高了 87 倍——你可能会问：这值得吗？

那要看情况了。写这篇文章我花了很长时间，也耗费了大量精力，特别是用微基准测试时出现的对齐问题是一个很大的难题。如果我正在优化一段生产代码，我可能会止步于基本优化这个环节。微调代码的效果可能不错，但要投入大量时间，而且这些优化在现代架构上的稳定性很差。

最后，本文中涉及的完整源代码可在这个 GitHub 存储库中获取：
https://github.com/HappyCerberus/1brc。