一、树的相关概念
在学习各种树的算法以及应用时,让我们先来学习一下树的相关概念。
✨1.1 结点的度
在树中,结点的度表示结点拥有的子树的数目,即结点有几颗子树,该结点就有几度。
下面来看图理解下。

在上图中,结点 A 有两棵子树,分别是 B 和 C,所以 A 的度为 2,B 有三棵子树,所以 B 的度为 3,同理,C 的度为 1,D 的度为 0。
✨1.2 叶子/终端结点
叶子结点是指度为 0 的结点,也称终端结点。
下面来看一个例子,如下所示:

上图中,红色结点 D、E、F、G 都是叶子结点/终端结点,因为它们都没有子树,度为 0。
✨1.3 非终端结点/分支结点
非终端结点是指度非 0 的结点,又称分支结点。
下面来看图理解下,如下所示:
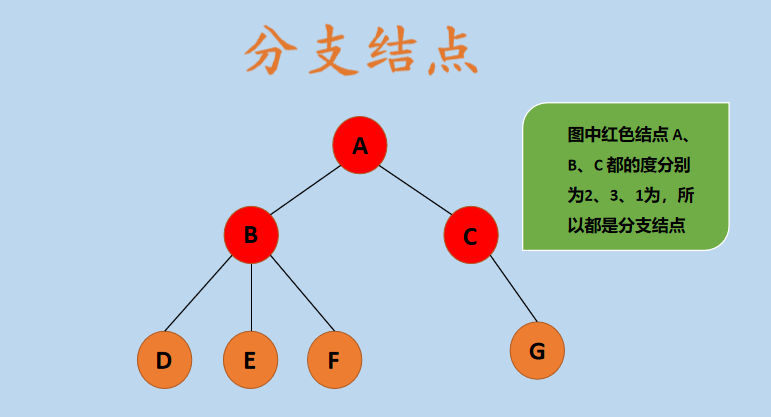
在上图中,红色结点 A 、B、C 都是分支结点,因为它们的度都是大于 0 的。
✨1.4 分支
分支是指父子结点之前的连接,二叉树最多有两个分支,这两个分支是父节点分别与左孩子和右孩子各有一个分支。来看图理解下,以二叉树为例。
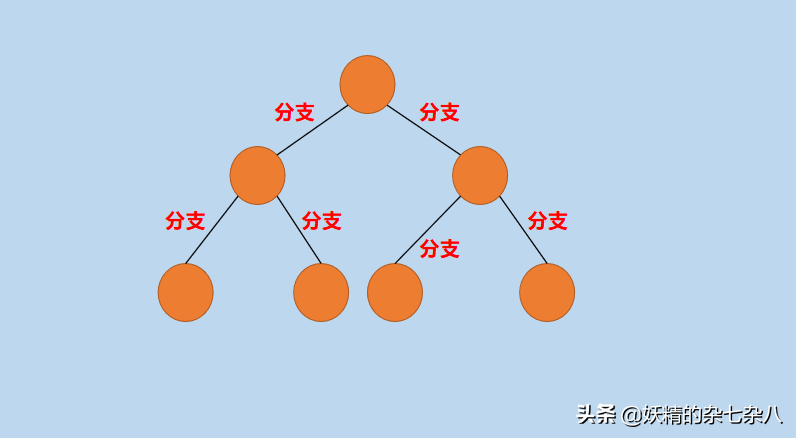
在上图中,分支都被标识了出来。
✨1.5 路径
路径是指树中任意一个结点到另外一个结点之前的分支组成的链路。

在上图中,标出了两条路径,分别是红色:A-B-D,紫色:G-C-F。
✨1.6 路径长度
路径长度是指在路径上的分支数目。

经常会有题目涉及求两个结点之前的路径长度。
✨1.7 树的路径长度
从树根到每一个结点的路径长度的总和。
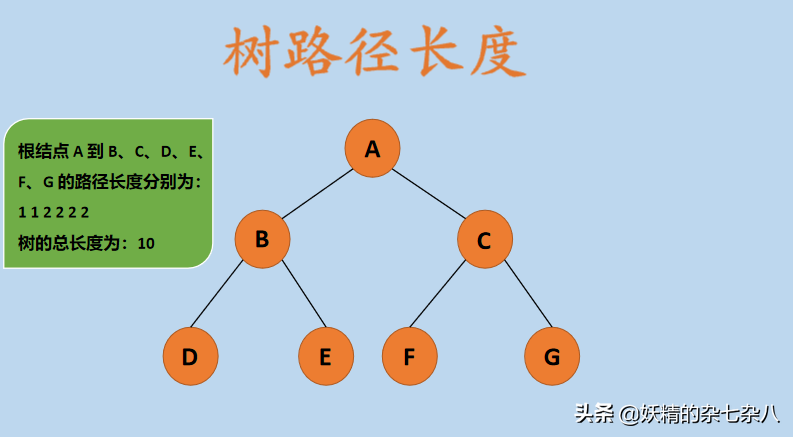
上图中,根结点 A 到其它节点 B、C、D、E、F、G的路径长度分别为:1 、1、2、2、2、2,所以树的总长度为 :1 + 1 + 2 + 2 + 2 + 2 = 10。
再来看一个例子,如下所示:
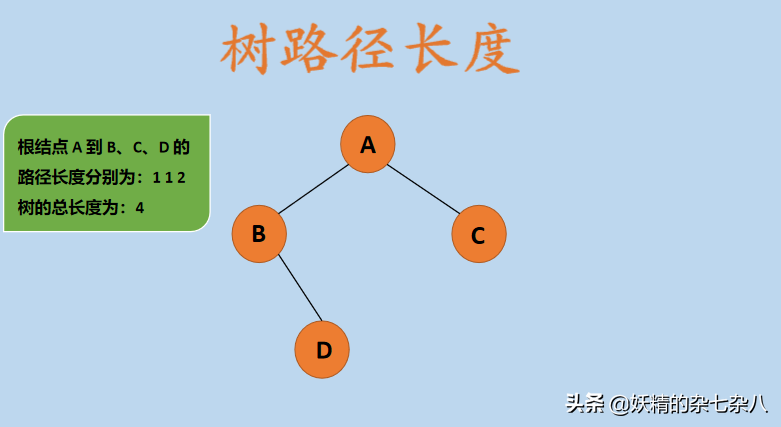
在上图中,根结点 A 到其它结点 B、C、D 的路径长度分别为:1、1、2,所以树的路径长度为:4。
✨1.8 树的带权路径长度
树的带权路径长度是指树中所有叶子结点的带权路径长度之和,使用如下公式计算:

其中,
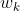
为叶结点 k 的权值,
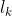
为叶结点 l 的路径长度。
来看一个实例,如下所示:
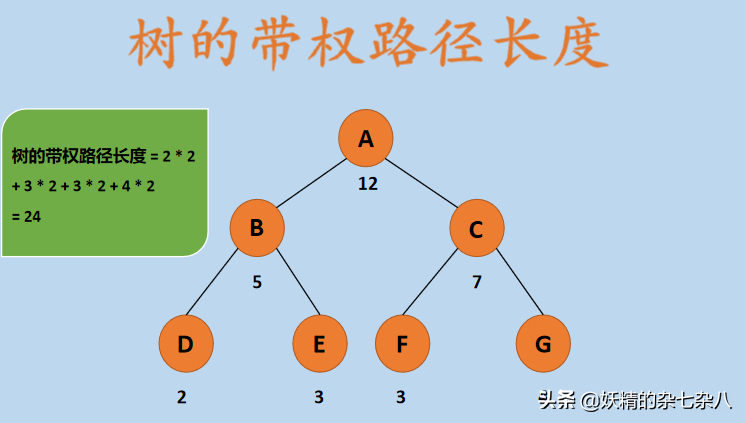
在上图中,叶结点分别为:D、E、F、G,其权值分别为:2、3、3、4,路径长度都为 2,所以树的带权路径长度:
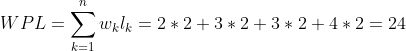
 鲁公网安备37020202000738号
鲁公网安备37020202000738号