来源:CreateAMind
AI of Brain and Cognitive Sciences: From the Perspective of First PrinciplesAI of Brain and Cognitive Sciences: From the Perspective of First Principleshttps://arxiv.org/pdf/2301.08382如今,我们已经见证了AI在各种应用中的巨大成功,包括图像分类、游戏、蛋白质结构分析、语言翻译和内容生成。尽管这些强大的应用,我们日常生活中仍有许多任务对人类来说非常简单,但对AI来说却极具挑战性。这些任务包括图像和语言理解、少样本学习、抽象概念以及低能耗计算。因此,从大脑中学习仍然是一条有前景的道路,可以为下一代AI的发展提供启示。
大脑可以说是宇宙中已知的唯一智能机器,它是动物在自然环境中生存进化的产物。在行为层面上,心理学和认知科学已经证明,人类和动物的大脑可以执行非常智能的高级认知功能,如灵活学习、长期记忆和在开放环境中做出决策。在结构层面上,认知和计算神经科学揭示了大脑具有极其复杂但优雅的网络形式来支持其功能。多年来,人们一直在收集关于大脑结构和功能的知识,这一过程随着全球范围内大型脑项目的启动而加速。那么,AI最应该从大脑中学到什么?
在这里,我们认为在现阶段,大脑功能的一般原则是最有价值的东西,可以启发AI的发展。这些一般原则是大脑提取、表示、操作和检索信息的标准规则,它们是大脑执行其他更高认知功能的基础。在某种意义上,它们是指导大脑运行的原则,我们称之为大脑的第一原则。
本文收集了北京智源人工智能研究院(BAAI)“脑与认知科学AI”研究团队总结的六个第一原则。它们是吸引子网络、临界性、随机网络、稀疏编码、关系记忆和感知学习。在每个主题上,我们回顾了其生物学背景、基本属性、潜在的AI应用以及未来的发展。
大脑由大量神经元组成,这些神经元通过突触形成各种网络。普遍认为,单个神经元的计算相对简单,而神经网络的动力学完成了大脑的功能。简而言之,神经网络接收来自外部世界和其他脑区的输入,其状态演化以进行信息处理。因此,动力系统理论是一个有价值的数学工具,用于量化大脑如何通过网络进行计算。
动力系统描述了一组变量如何随时间演化,这为研究复杂行为提供了一个强大的数学框架。通常,一个简单的确定性动力系统可以描述为:
在一个动力系统中,不同的状态演化规则和变化的外部输入可以在动力系统中产生多样的动力学现象。在一个循环连接的神经网络中,神经群体的发放率向量在网络的状态空间中演化并形成一条轨迹。如果一个状态向量的所有邻近状态都流向它,则称该状态向量为稳定吸引子。具有稳定吸引子的网络称为吸引子网络。类似地,网络状态可能流向一个闭环轨迹并产生周期性响应。这样的闭环轨迹称为极限环吸引子,具有这种吸引子状态的网络称为振荡吸引子网络。还有其他吸引子动力学,如鞍点和混沌吸引子。这些多样的吸引子动力学使得神经系统能够执行各种大脑功能[1,2,3,4,5,6]。在这里,我们的重点是具有稳定吸引子状态的吸引子网络,我们认为它们构成了大脑信息表示、操作和检索的基础。直观地思考,吸引子是神经网络中唯一能够使神经系统在环境中普遍存在的噪声和大脑中可靠地存储信息的状态。对吸引子动力学的研究有着悠久的历史。早在1972年,Shun-ichi Amari就研究了一个循环连接的神经网络,并发现它可以表现出离散的吸引子动力学[7]。这种现象后来被John Hopfield重新发现,并被称为Hopfield模型[8]。Hopfield证明,Hopfield模型可以将一个模式存储为网络的稳定吸引子,这解释了大脑的联想记忆。
连续吸引子神经网络(CANNs)是离散吸引子网络的扩展,其中吸引子在状态空间中连续分布。CANNs首先由Shun-Ichi Amari引入[9],后来成功应用于解释视觉皮层的方向调谐[10]、头部方向表示[11]和空间导航[12]等。到目前为止,离散和连续吸引子网络已被广泛用作文献中的典型模型,用于阐明各种大脑功能。
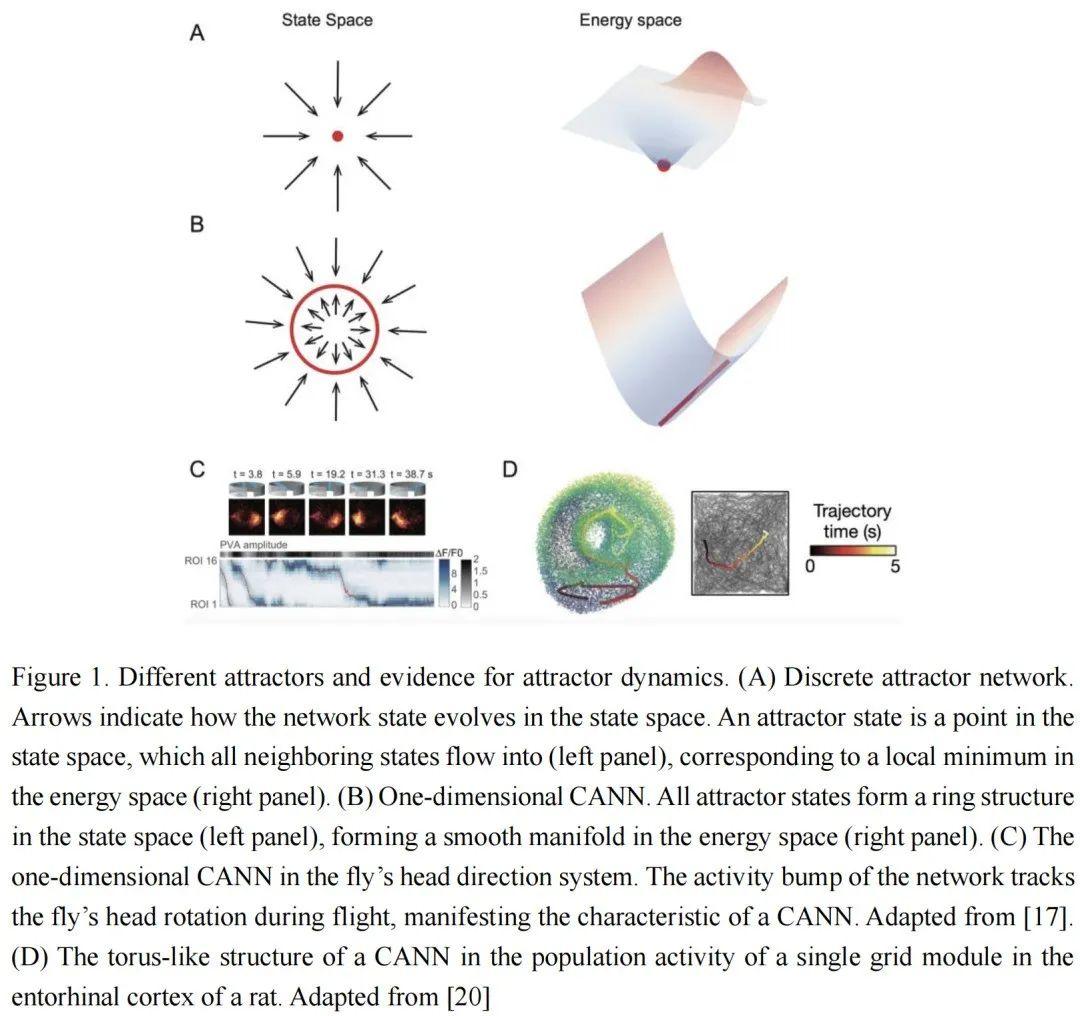
我们可以将具有稳定状态的吸引子网络大致分为两类:离散吸引子网络和连续吸引子网络,如图1A-B所示。在神经网络中,状态向量对应于网络状态空间中的一个点,其所有邻近状态都演化到该点。因此,这个状态向量是一个吸引子,对应于网络能量空间中的局部最小值,如图1A所示。在离散吸引子网络中,每个吸引子都有自己的吸引域。从随机状态开始,网络的循环动力学降低能量,直到将网络状态驱动到具有局部最小能量的邻近吸引子状态。这种离散吸引子动力学的特性使得网络能够纠正输入噪声并检索干净的记忆表示。离散吸引子网络常用于建模工作记忆、长期记忆和决策等。
与离散吸引子模型不同,CANN中的吸引子在状态空间中连续分布,形成一个平滑的流形,如图1B所示。这一特性使得CANN中的吸引子状态能够快速转移到附近的状态,称为中性稳定性。这为CANN带来了许多吸引人的计算特性[3,4,12],如路径积分、证据积累和预测跟踪。在结构上,神经元之间突触连接的平移不变性,即两个神经元之间的连接强度由它们之间的距离而不是特征空间中的偏好位置决定,是CANN的关键特性。
值得注意的是,离散和连续吸引子网络都是数学上的理想化模型。在自然神经系统中,很可能采用介于离散和连续吸引子网络之间的网络结构来编码信息,这种结构具有部分重叠的计算特性,即相对可靠地检索信息(如离散吸引子动力学)和相对快速地改变状态(如连续吸引子动力学)。
实验研究已经积累了大量证据,证明了大脑中存在吸引子动力学[13,15,16,17,18,20,21]。早在1971年,Fuster等人[13]就发现,在延迟反应任务的记忆保持期间,许多前额叶神经元持续发放脉冲。这些持续活动被认为在工作记忆中起着基础性作用,并且是吸引子动力学的指示[14]。与离散吸引子相比,连续吸引子具有更可预测的特征,已在不同皮质区域(如海马体及其相关区域)中发现。例如,头部方向系统可以整合头部旋转速度和外部线索信息来编码头部方向[15]。
CANN成功地用于模拟头部方向系统,该系统通过连续吸引子编码头部方向的角度。最近的研究[16]发现,果蝇头部方向系统中的神经元形成了一个与一维CANN完全相同的环状拓扑结构。除了结构相似性外,Kim等人[17]对飞行果蝇头部方向系统中的神经元进行了大规模群体记录。他们发现,该系统的动力学特性也与CANN非常一致,例如,系统中的局部活动凸起可以通过外部线索触发。随着果蝇头部的转动,凸起会平滑地跟踪头部方向(图1C)。凸起可以在黑暗中作为吸引子保持。此外,当创建新的凸起时,它会抑制先前位置的凸起。当在凸起的邻近位置施加刺激时,凸起活动会漂移到刺激位置。上述现象是一维CANN的特性。二维CANN也在动物(如啮齿动物)的海马体和内嗅皮层中发现。在海马体中,位置细胞在动物访问环境中的某些特定位置时发放,并被认为形成了空间位置的内部表示。它们表现出许多吸引子特性,如在黑暗中持续存在[18],这可以通过CANN很好地解释[19]。在内嗅皮层中,网格细胞编码抽象的空间位置,并形成规则的三角形网格放电模式。与头部方向系统类似,网格细胞网络可以整合运动和视觉线索来表示空间位置[12,19]。为了解释周期性网格模式,CANN预测网格细胞的状态在状态空间中形成一个拓扑环面。最近,Gardner等人[20]在行走和睡眠期间对网格细胞进行了大规模记录,并确认了来自同一模块(共享相同周期和方向的细胞)的网格细胞群体活动形成了一个环面拓扑结构(图1D)。此外,CANN不仅涉及空间导航,还涉及其他认知功能,如证据积累。例如,Mante等人[21]发现,当猴子执行依赖于上下文的决策任务时,随着证据的积累,猴子前额叶皮层的群体状态沿线吸引子演化,直到达到决策阈值。
总之,积累的实验和建模证据表明,吸引子网络可以被视为大脑用于信息处理的一种典型计算模型。
吸引子神经网络已被广泛用于建模大脑功能。在这里,我们回顾了它们在信息表示中的基本属性,这些属性奠定了它们在认知功能中的作用基础。
吸引子网络可以鲁棒地表示信息。在离散吸引子网络中,记忆信息作为吸引子状态存储。给定一个部分或带有噪声的线索,网络动力学演化到一个吸引子状态,并检索相应的记忆。不同的吸引子对应于不同的局部能量最小值,并有自己的吸引域。如果噪声扰动不足以将网络状态推离吸引域,吸引子状态是稳定的。因此,记忆信息被鲁棒地编码。与离散吸引子网络不同,CANN中的吸引子在网络状态空间中形成一个平坦的流形,并且对噪声具有部分鲁棒性。如果噪声扰动与流形正交,网络状态通过吸引子动力学保持稳定。然而,如果噪声扰动沿着流形,网络状态将在吸引子流形上扩散,从一个吸引子移动到邻近的吸引子。为了防止CANN中的记忆漂移,Lim等人[22]提出了一种依赖于负导数反馈的机制来保持吸引子状态的稳定性。
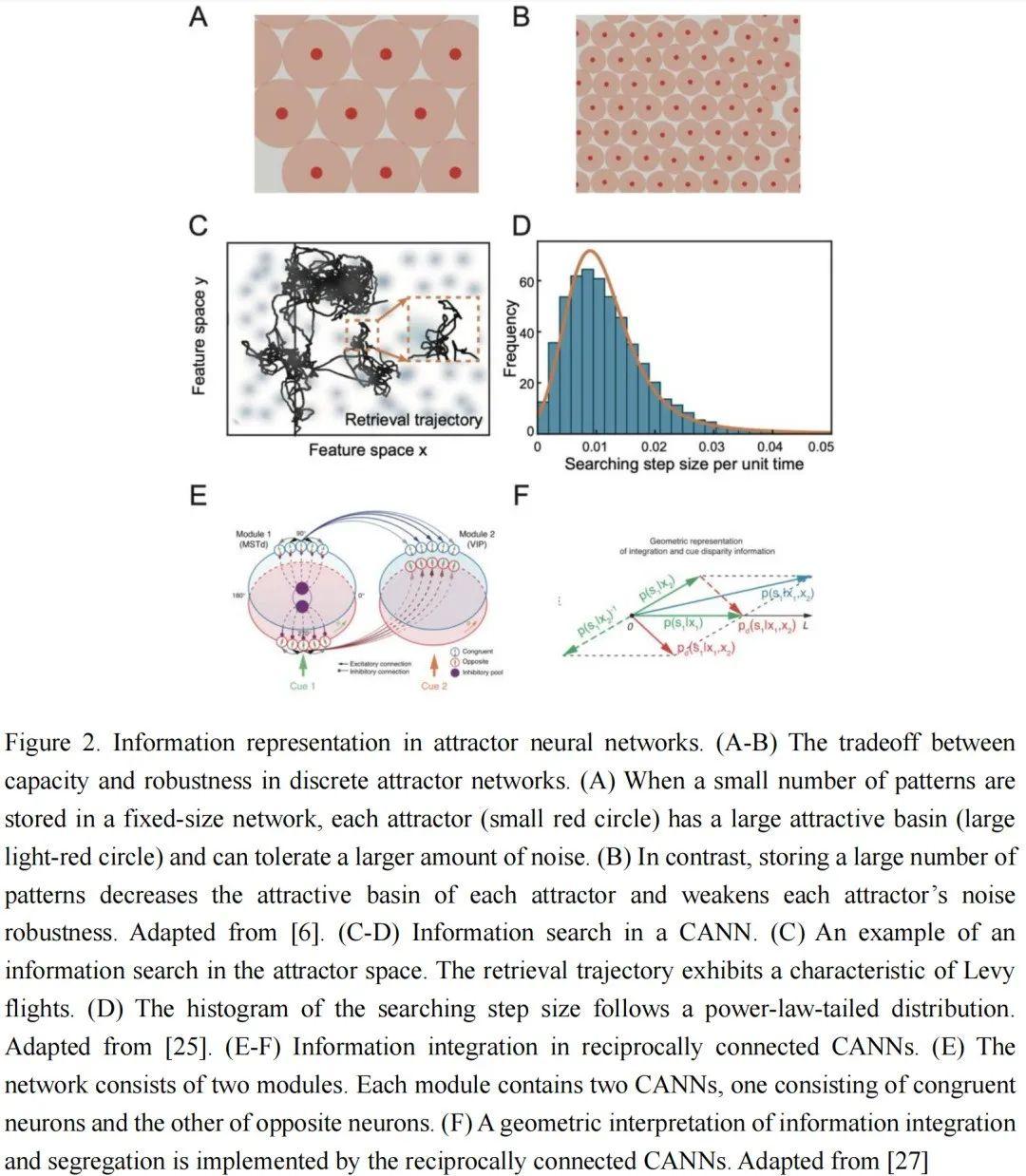
记忆容量指的是吸引子网络中可以可靠存储的记忆数量。有几个因素影响吸引子网络的记忆容量。一个是噪声。当网络中存储了太多记忆时,每个吸引子的吸引域缩小,这降低了吸引子对噪声的容忍度,如图2A-B所示。另一个因素是记忆相关性。当记忆模式高度相关时,它们会相互干扰并破坏记忆检索。对于N个神经元的Hopfield模型,如果所有记忆都是随机模式,其记忆容量约为0.14N。然而,当模式高度相关时,邻近的吸引子合并为一个,这引入了错误的表示,称为虚假吸引子。此外,当学习的记忆模式数量超过Hopfield模型的容量时,所有现有吸引子的稳定性将被破坏。
为了增加吸引子网络的记忆容量,已经提出了许多方法,从学习规则到网络结构,如基于新颖性的Hebbian规则[23]和模块化Hopfield网络[24]。
除了大记忆容量外,一个好的信息处理系统还需要高效的信息搜索。在吸引子网络中,记忆通常以内容可寻址的方式检索,即网络通过吸引子动力学执行相似性计算,并检索与线索最相似的记忆。在大容量网络中,从大量吸引子中找到正确的记忆是具有挑战性的。例如,在自由记忆检索任务中,参与者需要尽可能多地搜索和回忆动物名称。一个好的回忆策略是局部记忆搜索和记忆空间中的大跳跃的适当组合,表现为Levy飞行行为。Dong等人[25]证明,在具有噪声神经适应的CANN中,网络状态的动力学显示出交替的局部布朗运动和长跳跃运动,表现出与Levy飞行行为相似的最佳信息搜索行为,如图2C-D所示。吸引子网络还可以相互作用,以完成模态之间的信息整合。最近,Zhang等人研究了相互连接的CANN如何实现多感官信息处理[26,27],如图2E-F所示。在他们的模型中,他们考虑每个模块包含两组神经元,每组神经元形成一个CANN,它们的调谐函数在模态输入方面要么一致要么相反。他们表明,具有一致神经元的耦合CANN实现信息整合,而具有相反神经元的耦合CANN实现信息分离,它们之间的相互作用有效地实现了同时的多感官整合和分离。这项研究证明,互联的吸引子网络可以支持皮质区域之间的信息交流。
由于篇幅限制,我们只介绍了一些吸引子网络的基本属性。在应用中,当网络结构中引入额外元素时,吸引子网络可以表现出更丰富的动力学行为,并具有相关的吸引人的计算特性。例如,具有脉冲频率适应(SFA)的CANN可以执行预测跟踪[28],具有反馈连接的CANN可以表现出振荡跟踪行为[29],具有噪声SFA的CANN可以实现基于采样的贝叶斯推断[30]。
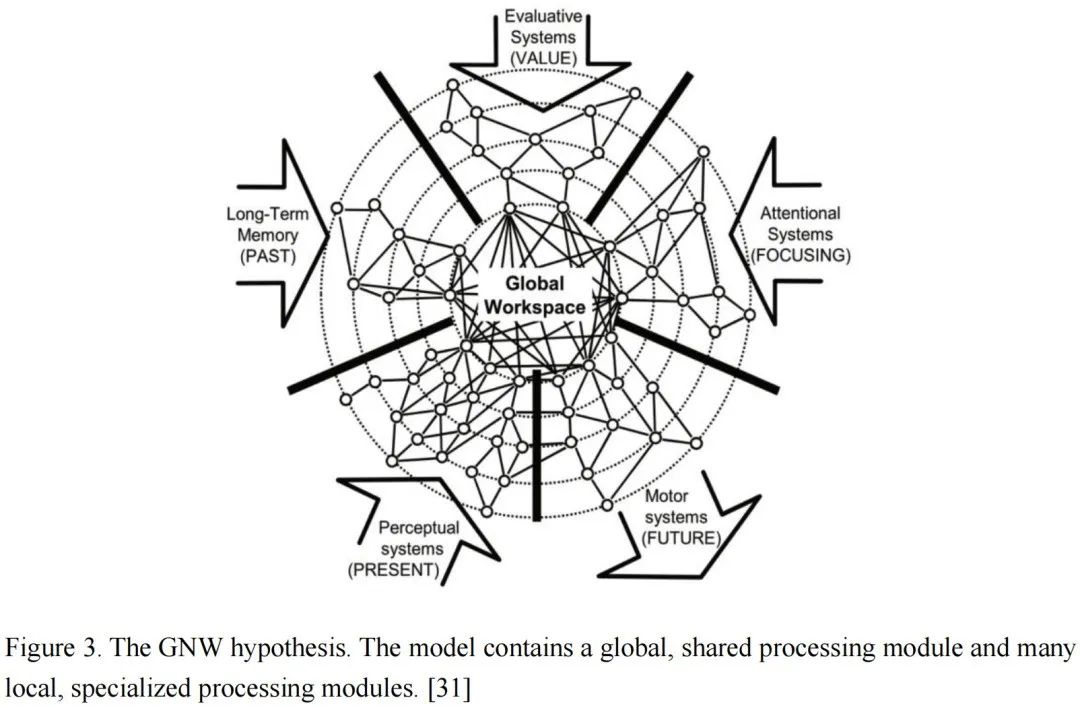
在过去几年中,由于数据和技术的限制,该领域的计算建模主要集中在研究单个神经元和局部电路的动力学和功能上。最近,随着技术进步和全球大型脑项目的推动,大量关于大脑结构和神经活动细节的数据正在涌现。现在是时候构建大规模网络模型来模拟更高认知功能了。吸引子网络作为神经信息处理的典型模型,为我们完成这一任务提供了基础。在这里,我们以全局神经工作空间理论(GNW)[31]为例,讨论吸引子网络的潜在应用。GNW提出了一个框架,说明大脑如何实现意识。根据GNW,大脑被分为一个共享的全局处理模块和许多分布式的专门处理模块,如图3所示。每个独特的模块处理来自一种模态的信息,如视觉、听觉、嗅觉或运动系统。相比之下,全局模块接收并整合来自所有专门模块的信息,同时将整合后的信息广播回这些局部模态。为了实现这一目标,需要一个抽象的信息表示接口,使不同模块能够相互通信。从这个意义上说,CANNs作为实验和理论研究中已被证明的典型模型,自然地作为模块之间表示、转换、整合和广播信息的统一框架。未来研究这一问题将会非常有趣。Zhiqiang Chen, Jinying Gao, Yu Zhu, Shan Yu*临界性框架是理解和分析复杂系统的有力工具,因为物理学和自然界中的许多系统都处于临界状态。在过去的20年里,研究人员发现大脑中的生物神经网络接近临界状态,这为研究脑动力学提供了新的视角。众所周知,临界状态对脑活动/功能至关重要,因为它优化了信息传输、存储和处理的许多方面。此外,一些脑疾病被认为与偏离临界状态有关,这也为诊断和治疗这些疾病打开了新的窗口。在人工智能领域,临界状态框架用于分析和指导深度神经网络的结构设计和权重初始化,表明接近临界状态可能是神经网络计算的基本原则之一。
在统计物理学中,具有相同物理和化学性质的材料系统中的均匀状态称为相[1]。例如,水可以处于固相、液相或气相。当温度变化时,水可以从一个相变为另一个相,这称为相变[2,3,4]。临界状态是一种所谓的二阶相变,表明系统从有序相过渡到无序相。在有序和无序之间的边缘,或“混沌的边缘”,临界状态表现出许多特殊性质。
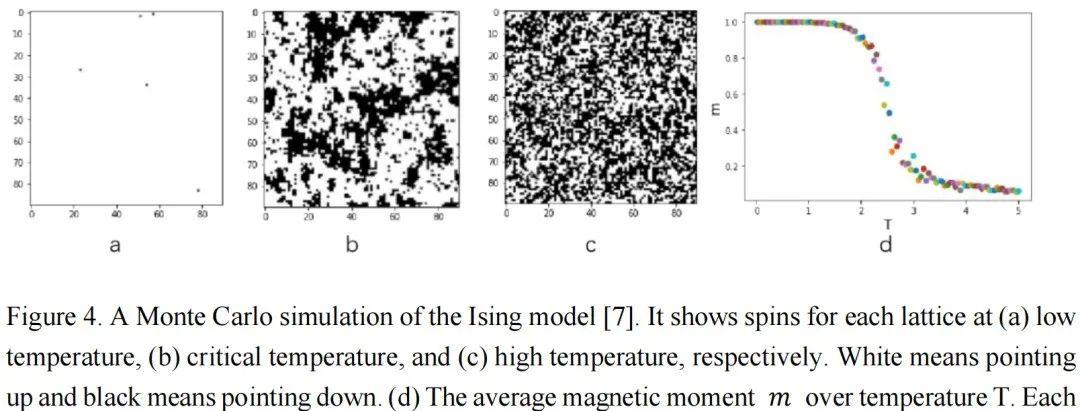
图4通过Ising模型的模拟展示了铁磁材料的相变过程和临界状态[5,6,7,8]。在Ising模型中,自旋相互作用和热运动的竞争导致有序和无序相。图1a和1c分别显示了低温下的有序相和高温下的无序相。当温度从低到高变化时,如图1d所示,系统将经历相变。在相变边缘的温度下,如图1b所示,有序和无序处于平衡状态,两者都不能主导整个系统。在这个温度下,系统极其复杂,处于所谓的临界状态。在有序或无序相中,域大小[9]的分布分别集中在较大或较小的尺寸上。但在临界状态下,域大小几乎分布在所有尺寸上。不同尺度的分布是自相似的,这意味着分布是分形的[10]和无标度的[11]。这种自相似分布可以用幂律[12]数学形式化:?(?) ∝ ?−?。如果我们在对数-对数坐标系中使用,分布将呈现为一条直线。幂律分布是临界状态的一个重要特征。当系统处于临界状态时,许多统计变量服从幂律分布。除了在Ising模型或其他系统中精确调整温度或控制参数以达到临界状态外,一些系统可以自发地达到临界状态,这称为自组织临界性(SOC)。一个著名的SOC模型是沙堆模型[13,14]。在这个模型中,沙子缓慢地堆积在一个表面上,沙堆的斜率逐渐增加。当达到临界斜率时,添加更多的沙子会使沙堆崩塌,形成各种大小的沙崩,使沙子离开沙堆,从而回到临界斜率。这些沙崩的大小服从幂律分布。自SOC提出以来,它已被用于解释许多复杂现象,包括经济系统的波动[15]、选举中的投票[16]、脉冲星[17]、黑洞[18]等。重要的是,越来越多的研究表明,大脑可能也处于自组织临界状态[19,20]。在下一章中,我们将详细介绍相关研究。
在过去的二十年中,通过在体外培养的脑组织或体内完整的大脑中记录神经元活动,许多实验表明皮层网络也可以自组织成临界状态,级联神经元活动的空间和时间分布近似服从幂律。这种现象称为“神经元雪崩”,为我们理解脑网络动力学提供了新的视角。它不仅在信息处理中具有许多计算优势,还为偏离临界状态引起的疾病的治疗和诊断打开了新的窗口。
在皮层网络中,每个神经元通过突触连接从大量周围神经元接收输入。当输入达到其阈值时,将产生动作电位,该电位将传递给其他神经元,导致其他神经元放电。Beggs和Plenz[21]发现了生物神经网络和沙堆模型之间的共性,并首次通过脑组织中的多电极阵列记录证实了临界大脑的猜想。他们发现神经元雪崩的大小和寿命都服从幂律,这是临界状态的一个重要特征。后来,其他研究人员在不同物种的不同大脑皮层中记录了神经元活动,在清醒和麻醉状态下重新确认了网络自发活动中神经元雪崩的幂律分布特征。这表明脑网络接近临界状态是一个普遍特征,兴奋性和抑制性的平衡在帮助维持临界状态中起着关键作用[22]。为了检查神经元雪崩是否是自发神经活动的独特现象,Yu等人[23]在猴子的前运动和前额叶皮层中记录了运动和认知任务期间的细胞外单位活动和局部场电位,结果表明参与主动信息处理的网络活动也保持在接近临界状态,表明神经元雪崩是休息和行为状态下神经活动的统一现象。
幂律分布是临界状态的有力证据[24]。然而,仅凭幂律不能被视为临界性的定义。许多显然不处于临界状态的系统也可以生成幂律分布[25]。幸运的是,存在超越幂律分布的其他证据可以佐证临界性的识别。如果在Ising模型或其他临界系统中调整温度或“控制参数”,幂律分布将迅速消失,并发生相变[24]。而与临界状态无关的幂律分布不会经历相变[24]。在神经系统中,兴奋性和抑制性之间的平衡可以作为控制参数。当通过药物阻断兴奋性或抑制性递质时,E-I平衡的变化会破坏原有的幂律分布,并呈现两种不同的相(即亚临界和超临界,分别)[22]。此外,当系统处于临界状态时,会出现许多分形特征。当缩放不同持续时间的雪崩形状时,会出现干净的折叠,正如在临界状态下所预期的那样[26]。来自多个视角的这些证据很好地汇聚在一起,并提供了强有力的支持,表明大脑确实组织在接近临界状态。
为什么大脑处于临界状态?进一步的研究表明,处于临界状态的网络在信息传输、存储和处理方面具有明显的优势。这些优势已在临界模型和生物实验中得到证实。2006年,Kinouchi等人[27]构建了一个简单的神经网络,将每个神经元的局部分支比率限制为1,此时网络被认为达到临界状态。通过建模发现,在这种分支比率下,网络对输入的表示具有最佳的动态范围。当分支比率设置为小于1时,网络被认为是处于亚临界状态,此时网络不能清晰地区分弱输入。当分支比率设置为大于1时,网络被认为是处于超临界状态,此时网络很快会达到饱和。后来,Shew等人[22]在多电极阵列表面培养切片,并调节培养环境以达到临界状态,从而证明处于临界状态的系统最能敏感地感知跨越几个数量级的信号幅度。此外,其他研究人员还证实,处于临界条件的系统具有优化的计算能力[28]、最大的记忆库大小[29]和最大的信息传输保真度[30]。Hu等人[31]证明,当通过多巴胺将网络调节到临界状态时,工作记忆(WM)在生物学上合理的工作记忆模型[32]中具有最佳性能和最大敏感性/灵活性。
大脑中偏离临界状态的大偏差可能导致癫痫[33]、爆发抑制[34]和精神分裂症[35],这些疾病表现为临界状态的破坏,从而干扰信息的正常传输或处理。计算模型的快速发展使研究人员能够使用临界状态框架来模拟上述疾病,从而为理解神经系统复杂实验记录数据提供了新的视角。Dean等人[36]开发了一个系统,可以跟踪癫痫发作通过分岔空间的路径,这可以作为长期预测和诊断癫痫发作的手段。Xin等人[37]对重度抑郁症患者的静息状态功能磁共振成像数据应用了临界动力学分析。他们发现,重度抑郁症患者的宏观脑网络偏离临界状态并维持亚临界状态。重要的是,电休克疗法(ECT)恢复了临界状态,并伴随着抑郁的缓解,这为重度抑郁症本身和ECT的治疗效果提供了机制解释。尽管仍处于探索阶段,这些研究为神经系统疾病的诊断和治疗打开了新的窗口[38]。
鉴于临界状态在分析包括神经系统在内的许多复杂系统中的成功应用,一些研究人员也尝试使用临界状态来研究人工神经网络,例如改进储层计算和增强深度神经网络。
储层计算(RC)通常指的是循环神经网络(RNN)的一种特殊计算框架,其中可训练参数仅存在于最终的读出层,即非循环输出层,而所有其他参数在随后的计算中随机初始化并固定[39,40,41,42](另见第3章随机网络)。目前,RC模型已成功应用于许多计算问题,如时间模式分类、识别、预测和动作序列控制[43,44]。RC模型只有在网络处于临界状态时才能很好地工作,有时也称为“回声状态”[39]。这意味着我们需要仔细初始化网络连接[45,46]。受生物神经网络中短期突触可塑性(STP)的启发,Zeng等人[45]在RC模型中实现了由短期抑制(STD)引起的自生临界性(SOC)方案,该方案自动将RNN的状态调整到接近临界性。STD大大增强了神经网络的鲁棒性,使其能够在维持由临界性赋予的最佳性能的同时适应长期突触变化。它还表明大脑用于在不同时间尺度上组织可塑性以维持信息处理的最佳状态(临界状态),同时允许内部结构变化以进行学习和记忆的潜在机制[45]。
与浅层网络相比,深度神经网络取得了巨大的成功。为了从理论上解释这一现象,Poole等人[47]将黎曼几何与高维混沌的平均场理论相结合,揭示了深度随机网络中随着深度增加的指数表达能力的来源是混沌状态(临界状态)的瞬态变化。此外,他们证明浅层网络中不存在这种特性。这一发现对网络结构设计具有重要意义,并为现有深度神经网络的优越性能提供了理论基础。受此工作启发,Schoenholz等人[48]开发了深度网络梯度的平均场模型,并表明深度网络只有在保持在或接近临界状态时才能得到良好训练。Poole等人[47]建立的有序和混沌相位恰好对应于梯度消失和爆炸的区域。理论分析表明,在混沌边缘的权重初始化,即深度网络的输入-输出雅可比矩阵的均方奇异值应保持在接近1,这导致学习速度大幅提高[49]。此外,Pennington等人[50,51]采用自由概率理论分析了计算输入-输出雅可比矩阵奇异值的整个分布,将深度、随机初始化和非线性激活函数作为独立变量。然而,上述研究都没有涉及学习规则。Oprisa等人[52]发现,神经元的激活频率不遵循幂律分布,经典深度神经网络中不会自发出现临界状态。他们指出,设计学习规则以在网络中诱导临界状态是一个基本缺失的部分。此外,Farrell等人[53]也发现,强混沌RNN(超临界性)更擅长学习扩展和压缩的平衡,从而实现更好的性能。因此,是否处于临界状态总是有帮助仍然是一个开放的问题。
临界状态为我们研究生物和人工神经网络提供了新的视角。目前,临界性框架不仅用于理解神经动力学和脑疾病,还用于分析深度神经网络的运行并指导进一步改进的设计。通过理论分析和数值模拟,我们知道网络的临界状态可以通过一些简单的控制参数来控制,如分支比率、谱半径和输入-输出雅可比矩阵的奇异值。这使得通过易于观察的统计数据来分析或调整复杂网络的整体行为成为可能。我们相信,临界性框架将在帮助我们更好地理解施加在人工神经网络上的约束以及设计更好的架构和动力学规则以提高其在复杂信息处理中的性能方面发挥更加重要的作用。Longsheng Jiang, Sen Song*### 3.1 引言:维度自Hubel和Wiesel发现神经元对条形方向的调谐[1]以来,神经生理学家一直致力于寻找具有对单一特定刺激特征清晰调谐曲线的神经元。然而,在这一过程中,神经生理学家常常发现自己处于一种困惑的境地,即许多观察到的神经元同时非线性地反映不同的特征[2]。这些神经元被称为具有非线性混合选择性[2,3,4,5,6,7]。为了理解这一点,神经生理学家转向基于群体的神经元分析[8,9,10]。群体编码在高维状态空间中表示神经响应,其中每个神经元的活动代表空间的一个维度[另见第1章吸引子动力学]。在这个神经空间中,更多的信息可以被区分地解码[10]。
非线性混合选择性神经元的存在增加了表示的维度。结果,原本线性不可分的表示变得线性可分[3],并可以被大脑的下游结构进一步处理[11,12]。为了确保高维度,混合选择性也需要多样化[3]。为了研究大脑中支持多样化混合同时保持简单的电路,一些研究人员提出随机网络可能在工作[13,14,15,16,17,18,19]。在随机网络中,神经元连接的突触权重从某些分布中随机采样。这些连接将信号混合作为下游神经元的输入。输入在神经元内经过非线性映射。通过这种方式,神经元被赋予了非线性混合选择性。连接的随机性赋予了混合的多样性。越来越多的生物学证据支持这一观点[20,21,22,23,24,25,26,27,28,29,30,31,32]。
早在1888年,Cajal[33]就发现了神经元细胞的两种不同结构特征:轴突,它直接穿过神经毡,以及树突,它们广泛延伸,仿佛试图接触尽可能多的穿过神经毡的轴突[34]。这种基本结构交织在一起的复杂神经网络,在脑区有限的空间内密集排列,暗示了一种分布式电路模型用于神经计算。在这个模型中,一个神经元尽可能多地向其他神经元发送和接收信号[35]。理想情况下,分布式电路模型规定了在物理极限下神经元之间的全连接。虽然全连接在生物学上不可行[36],但可以使用随机连接来近似全连接[35]。
这种随机性在动物的大脑中已被观察到,其中随机连接的显著证据来自嗅觉系统。随机连接从触角叶中的气味特异性小球到蘑菇体中的Kenyon细胞(KCs)[20]。这种连接违背了连接中的任何解剖和功能结构。即使是同一只苍蝇大脑的两个半球,连接结构也不同[21]。一个实现随机连接和其他生物约束的KC模型再现了实际KC的响应[22]。同样,在啮齿动物的嗅觉皮层中,从嗅球到梨状皮层(PCx)的连接是随机的[23]。一个PCx的随机网络模型很大程度上再现了气味表示之间的成对关系。
另一个典型的例子是小脑[24,25,26]。从苔藓纤维到颗粒细胞再到浦肯野细胞的路径涉及随机连接。苔藓纤维将信号传导到小脑,随机连接到无处不在的颗粒细胞。然后,通过平行纤维,颗粒细胞连接到广泛延伸的浦肯野细胞的突触。浦肯野细胞作为小脑中的读出神经元。
尽管较少共识[27],但视觉系统中也有强有力的支持证据。猕猴视网膜中的视锥细胞到视网膜神经节细胞(RGCs)的功能连接对于感受野中心几乎是随机的,对于感受野周围是完全随机的[28]。在视觉通路中,随机性是猫的RGCs和外侧膝状核(LGN)中的中继细胞之间连接的特征。引入RGCs和中继细胞之间随机连接的模型匹配实验数据并促进了视觉空间的插值[30]。此外,猫的LGN到初级视觉皮层(V1)的连接也可能是随机的[31],因为具有随机连接的模型产生了方向图,并且模型感受野的特征与实验观察结果相匹配[31]。对于没有方向图的动物,如啮齿动物,方向选择性可以从LGN神经元和V1神经元之间的随机连接中出现[17]。这是因为ON和OFF细胞的感受野的空间偏移在皮层神经元上收敛。模型生成的模拟偏移与实验观察到的偏移相匹配。
除了感觉系统外,随机连接可能也存在于动作[13]、决策[32]和导航[15]的电路中。一个随机连接的前馈网络模拟了前运动皮层和初级运动皮层(M1)之间的连接[13]。该网络提供了一个罕见的例子,复制了M1中神经响应的规律性和异质性。异质性元素有助于从M1神经元活动中解码肌电图(EMGs)。一个具有随机连接权重的递归网络被用于模拟后顶叶皮层(PPC)在决策的证据积累任务中的行为[32]。这个简单的模型再现了实验数据中单神经元选择性的分布、成对相关性的模式等。在模拟果蝇的空间记忆网络中,随机网络可以支持持久的连续吸引子[15],从而可以记忆位置。如果随机网络确实意味着增加表示的维度,那么网络的架构应该反映这一目的。神经元群体允许的神经空间的最大维度是神经元的总数。为了增加维度,在完全随机连接的极端情况下,后连接神经元的群体应该大于前连接神经元的群体。因此,网络应该具有发散架构[26]。
发散架构确实存在于生物大脑中[37,38]。果蝇的触角叶到蘑菇体通路提供了一个清晰的例子。触角叶包含大约50个小球。大约150个投射神经元的一部分支配小球并投射到蘑菇体中的大约2500个KCs[39]。啮齿动物的嗅球包含大约1800个小球[40],而下游的PCx包含数百万个神经元[37]。在人类视觉通路中,来自LGN中100万个中继细胞的视神经投射到V1中大约1亿个皮层神经元[27]。在老鼠的小脑中,大约7000个苔藓纤维估计扩展到大约209,000个颗粒细胞,这些颗粒细胞是浦肯野细胞(即读出神经元)的前突触[41]。这些现象表明,通过具有随机权重的发散网络创建丰富的高维表示可能是一个潜在的计算原则。事实上,自20世纪90年代初以来,这一提示已经在人工智能(AI)中被遇到[42]。
AI中的随机网络指的是部分权重被随机初始化并且在训练期间不适应的人工神经网络(ANNs)。研究人员最初被这些网络吸引,要么是因为它们易于设置用于分析[43,44],要么是因为它们的训练速度更快[45]。然而,研究人员很快发现随机网络表现惊人地好;它们的测试准确率接近完全训练的模型[46],在短期预测、图像识别和生物医学分类等应用中[42]。受这些观察的启发,研究人员研究了各种随机网络的特性。
两类网络被广泛研究。前馈网络和类似储层的递归网络[另见第2章临界性]。在前馈网络中,输入神经元以随机权重连接到一个尺寸大得多的隐藏层。在储层计算中,输入神经元连接到一个内部神经元的储层,这些神经元之间具有随机连接。前馈网络的例子包括随机向量函数链接网络(RVFL)[47]、径向基函数链接网络[48]、具有随机权重的前馈网络[49]、无传播算法[50]、权重无关网络[51]和随机CNN[52]。储层计算的例子包括回声状态网络(ESN)[53]、液态状态机(LSM)[54]和深度ESN[55](详见[56])。
所有这些模型共享三个特征:(1)隐藏层或储层创建输入的高维表示[57],(2)连接到输出神经元的权重需要线性优化[42],(3)网络性能对不同随机权重实现的鲁棒性[46]。从这些观察中可以得出的结论是,训练好的ANN的架构,而不是精细调整的连接权重,对任务性能负有更多责任。进一步的有趣研究表明,甚至架构本身也可以是随机的。由随机图生成器创建的架构在ImageNet上显示出良好的分类准确率(随机连接网络为79%,ResNet-50为77%)[58]。这些观察表明,随机性几乎不是一个简单的技巧,而是可能是机器智能的基本原则。这一点与我们在上面总结的神经科学中的类似猜想相呼应。随机网络的有效性和效率及其体现未发现计算原则的潜力因此激励了许多工作对其进行分析研究[5,37,41,59,60]。
随机网络在生物大脑或计算机中的目的是增加表示的维度。但高维度的确切好处是什么?对于?个不同的点,这些点在?维表示空间中变得线性可分的概率是[61]:随着?的增加,分离的概率也增加,使得下游解码更容易。为了收获解码优势,维度应该增加得相当快。为了阐明表示维度的增加,我们在这里关注一个简单的前馈网络。假设隐藏层有?个神经元,它们创建一个?维的隐藏空间。隐藏层中表示的维度?定义为[62]:其中??是隐藏空间中点的协方差矩阵的特征值。根据这个定义,如果每个维度是独立的并且具有相同的方差,那么? = ?。然而,如果维度是相关的,那么? < ? [41]。
维度?受网络架构的约束。假设输入层有?个神经元,输入层中的表示是?维。还假设每个隐藏神经元连接到?个输入神经元,并且连接权重是均匀的。当?和?很大时,在通过非线性激活函数之前,到达隐藏层的混合输入的维度?是[41]:对于固定的?,具有? ≫ ?的发散架构增加了?的值。如所见,?保证? ≤ ?,因为线性混合不能超过原始维度。然而,在非线性激活之后,表示维度?可以是? ≤ ? ≤ ? [41]。输入层和隐藏层之间的随机连接可以进一步加速维度的增加。如果连接权重从均值为?和方差为?2的分布中采样,并且当? ≫ ? ≫ 1时,混合输入的维度?是[41]: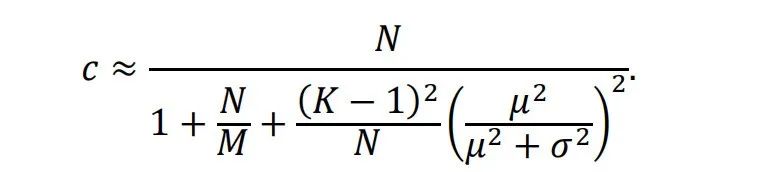

了解随机网络实际上实现了什么算法同样重要。Dasgupta等人发现,果蝇嗅觉电路的机制与计算机科学中的局部敏感随机哈希算法非常相似[59]。也就是说,局部敏感哈希和嗅觉电路保留了表示之间的相似性[64]。研究人员发现,在深度学习中添加随机哈希显著提高了训练效率(使用5%的计算量,同时保持1%的准确性)[65]。因此,有人认为局部敏感哈希可能是大脑中的一个计算原则。生物学证据、工程实践和理论分析似乎指向一个观点,即分布式随机网络足以实现认知功能。然而,这一观点过于简化。随机网络必须与其他网络特征结合才能实现复杂功能。这些特征包括收敛读出[66]、可塑性[67,68]、兴奋-抑制平衡[14,44]和稀疏性[5,14,37]。
在神经电路中,发散的随机连接层通常后面是收敛连接到读出神经元[22,38]。收敛结构对于维持神经表示的个体间一致性是必要的[66]。由于连接是针对个体大脑随机初始化的,两个大脑几乎不可能具有相同的连接模式。因此,表示的个体间一致性在神经元水平上丢失。也就是说,相同的刺激在个体中激活不同的神经元。然而,个体间一致性在群体水平上仍然存在。将群体的活动收敛到一个读出神经元继承了一致性[66]。
人们普遍认为,随机层之后的收敛连接是可塑的。它们依赖于经验[20]并需要训练[42]。可塑性对于个体间一致性至关重要。在两个随机网络的实现中,只有对一个刺激进行Hebbian学习训练其收敛连接后,这些实现在整个刺激集上显示出一致的泛化[68]。此外,有人建议发散层的随机连接可能经历Hebbian学习[67]。在随机连接中添加这一简单机制后,模型模拟的结果惊人地匹配了神经元群体的实验选择性剖面[67]。
除了收敛连接到读出神经元外,发散随机层的另一个显著特征是它受到反馈抑制,在果蝇[22]和啮齿动物[23]的嗅觉系统中,以及在小脑[26]中。抑制的一个可能功能是确保神经元的选择性。在一个神经元连接到数千个其他神经元的分布式网络中,如果所有连接都是兴奋性的,那么总输入的波动会被淹没[44]。抑制活动平衡了兴奋活动,使得预期的总活动为0[68]。因此,波动被突出,网络表现出高刺激选择性[14]。
抑制的另一个可能功能是在发散层中创建稀疏表示[另见第4章稀疏编码],这可能实现赢家通吃算法[59]。更高的抑制水平导致更稀疏的表示。稀疏性至关重要,因为它控制了网络在区分和泛化之间的权衡[5]。在高维状态空间中,发散层创建的区分需要区分点,而泛化需要分组点。计算模型的分析表明,高稀疏性导致较低的区分性但较高的泛化性[5]。事实上,稀疏性对神经电路很重要,因为它本身可能是一个生物计算原则[69,70]。
所有这些附加特征,包括收敛读出、可塑性、兴奋-抑制平衡和稀疏性,对神经电路都是不可或缺的。它们必须建立在发散随机层之上,而随机连接是前提。随机网络是产生神经生理学中常见混合选择性的最简单神经电路。尽管与功能只能从组织网络中产生的常识相悖,随机网络在过去几十年中在生物大脑的各种系统中被发现。同时,随机性在AI中被用作构建ANNs的计算高效方法。由于其独特性和有效性,随机网络吸引了许多理论研究,这些研究有助于揭示其背后的原则。
这些原则可以在三个概念层面上解释[71]。在计算层面上,随机网络像训练好的神经网络一样是通用函数逼近器。通过发散架构,随机网络创建高维状态空间,其中区分性解码更加灵活和可实现。在算法层面上,随机网络作为计算机科学中的局部敏感哈希算法工作。这些算法可以大大节省训练深度网络的计算需求。在实现层面上,随机网络是大脑中密集排列的神经毡中分布式网络的最可能物理实现。随机网络的原则不应被孤立地看待。它只有在与其他特征(包括收敛读出、可塑性、兴奋-抑制平衡和稀疏性)一起工作时才能完全发挥功能。因此,随机网络不应被视为或应用为孤立的电路。
过去十年的研究帮助我们认识到随机网络的重要性并澄清了一些关键概念。然而,仍有许多问题需要回答。在计算层面上,除了维度和稀疏性,我们几乎不知道随机网络中的表示。状态空间中的内在状态流形是什么样的?在算法层面上,随机采样权重的分布仍然是经验性的和任意的。如何指定这些分布?是否应该使用先验知识?生成的权重应该是固定的还是经过缓慢的Hebbian学习?在实现层面上,大脑也具有模块性,例如功能柱。模块性应如何与随机分布的网络结构协调?在回答这些问题时,我们对随机网络的知识将得到推进。届时,我们可能会确实确认随机网络代表了智能的一个基本原则。
Xiang Liu, Linlu Xu, Liangyi Chen*大脑是一个存储和处理信息的机器。为了实现这些功能,需要对外部信息进行准确的量化和合理的表示[1]。稀疏编码策略是实现这些目标的关键方式。大脑在多个层面上利用稀疏机制,包括视觉、嗅觉、触觉和其他感知层面,这些机制参与了皮质信息处理等过程[2]。讨论这些机制对于理解神经系统组织和智能形成的原则至关重要。
稀疏编码意味着在任何给定时间,只有极少数神经元放电,而总神经元数量的大部分处于静默状态[3]。因此,稀疏性是一个相对概念,没有明确的阈值。稀疏编码的优势在与两种更极端的编码方案——局部编码和密集编码[4]——相比时最为明显。局部编码有时称为独热编码:每个神经元仅参与编码一个项目,如“祖母细胞”的情况,任何两个项目之间的表示没有重叠。在另一个极端,密集编码是一种完全分布式编码:每个项目将由一个群体内所有神经元的联合活动表示[另见第3章随机网络]。稀疏编码介于两者之间,通常兼具两者的优势[5]。
稀疏编码在编码容量(以及能量效率)和解码难度之间提供了良好的权衡。由于局部编码不允许重叠,N个二进制神经元的群体最多可以表示N个不同的项目。随着更多神经元被招募来编码更多项目,将消耗更多能量。因此,大脑可用的能量为局部编码设置了上限。另一方面,密集编码通过允许N个二进制神经元编码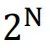 个项目,显著提高了表示能力。即使对于一个项目,只有少数(最多K个)神经元可能同时激活,如稀疏编码的情况,不同代码的总数也将是
个项目,显著提高了表示能力。即使对于一个项目,只有少数(最多K个)神经元可能同时激活,如稀疏编码的情况,不同代码的总数也将是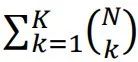 。与局部编码相比,这种配置节省了神经元,并以更少的能量编码相同的信息。然而,分布式代码的读出不简单,并且以生物学上合理的方式学习可能具有挑战性。相比之下,局部代码及其输出的关联可以通过简单的Hebbian机制建立;因此,如果神经活动模式是稀疏编码的,学习将更加高效[3, 6]。
。与局部编码相比,这种配置节省了神经元,并以更少的能量编码相同的信息。然而,分布式代码的读出不简单,并且以生物学上合理的方式学习可能具有挑战性。相比之下,局部代码及其输出的关联可以通过简单的Hebbian机制建立;因此,如果神经活动模式是稀疏编码的,学习将更加高效[3, 6]。稀疏编码还平衡了泛化和干扰。在局部编码中,每个模式与其他任何模式正交。由于不同模式之间没有相似性,因此不可能从一个模式泛化到另一个模式。密集和稀疏编码允许代码之间存在部分重叠和不同程度的相似性,从而实现具有相似代码的项目之间的泛化。然而,密集编码规定许多项目(如果代码空间被完全占用,最多可达所有项目的50%)可能激活一个神经元。这种广泛的调谐可能导致不同模式之间的干扰[7]。在学习过程中,形成一个新的代码模式与输出单元之间的关联可能会干扰与重叠代码和共享连接权重相关的老记忆[5]。稀疏编码可能有助于解决这种灾难性遗忘[8]并最小化模式之间的干扰[9]。在极端情况下,局部编码不会受到干扰,多个项目可以同时表示。
最后,稀疏编码明确表示自然刺激的结构,这些结构尖锐地调谐了神经元的响应。感受野类似于环境中遇到的频繁结构,因此只有少数神经元的激活就可以表示自然刺激。结合过完备基,稀疏编码可以产生自然刺激聚集的弯曲流形的分段平坦表示,简化了后续阶段的表示和分析[3]。这些优势支持生物体更高效的编码、传输和存储信息。
4.3 大脑中的稀疏编码
稀疏编码在神经系统中无处不在,尤其是在初级感觉皮层中。先前的研究表明,稀疏编码与视觉、听觉、嗅觉和体感系统有关[2,10,11,12]。此外,在运动和记忆相关的大脑区域中也发现了稀疏编码[13,14,15]。关于神经系统中稀疏编码的一些观点是,稀疏编码体现在三种形式中:群体稀疏性、生命周期稀疏性和连接稀疏性[16,17]。群体稀疏性意味着在给定时刻,一个群体中放电的神经元数量是稀疏的。生命周期稀疏性描述了神经元在其生命周期中稀疏放电[18]。以前,从代谢能量约束的角度推测,在大脑皮层中,大约0.5%到2%的神经元能够在给定时刻同时激活[19,20]。2018年,Tang等人直接测量了清醒灵长类动物大脑皮层的神经元群体激活的稀疏性。他们向猕猴展示大量自然场景图片,并使用大视野双光子显微镜同时记录猕猴初级视觉皮层浅层的神经活动。虽然只有0.5%的这些神经元对任意自然图片有反应,但每个神经元对不到0.5%的所有自然图像有强烈反应[12]。由于猕猴的V1神经元表现出高群体和生命周期稀疏性,神经元的高选择性可能在猕猴视觉皮层中执行稀疏编码。
生物大脑还表现出连接稀疏性,通常通过一组或一层神经元连接到另一层的百分比来衡量。根据多电极细胞内记录,锥体神经元在层间的局部互连性低于层内。例如,锥体神经元在同一层内的互连比率为1:10[21]或1:4[22],而在层间的比率跳到1:86[23]或1:29[22]。这种连接比率在物种和亚层之间有所不同,并且在实验测量之间略有差异,但总体属性是一致的。有趣的是,Carl Holmgren等人发现同一亚层内锥体神经元之间的连接比率较低,并且随着神经元之间距离的增加,连接性显著下降。这与中间神经元和锥体神经元之间的高连接比率形成对比,后者不会因物理距离的增加而改变[24]。因此,锥体神经元可能采用与中间神经元紧密全连接的方式,而在相互连接时不遵循相同模式。电子显微镜(EM)的最新进展允许精确重建皮层体积内的所有突触,这为建立神经元连接组提供了金标准。使用大体积串行EM,Wildenberg等人发现灵长类动物的皮层神经网络比小鼠更稀疏,这可能是由于突触维护成本的限制[25]。
关于稀疏编码在自然神经系统中如何实现,已经提出了许多理论和模型。Rozell和Olshausen[26]提出了一种局部竞争算法,将稀疏编码归因于同一区域内神经元之间的相互抑制。人们认为这种机制可能与压缩感知理论有关[27]。嗅觉系统中的稀疏编码具有类似的机制,并额外增加了反馈皮层[28],这种机制也出现在视网膜中。稀疏编码和稀疏神经活动实现了高效的信息压缩或维度降低。Ganguli指出,随机投影可以将高维稀疏信号投影到低维空间,而不会破坏原始信号的结构[27]。这些随机投影可以简单地作为神经系统中的随机突触连接矩阵来实现[另见第3章随机网络]。通过这种方式,稀疏编码信号的神经生物学实现可能是微不足道且普遍的。
4.4 稀疏编码的理论研究和应用
稀疏性和稀疏编码一直备受关注。Barlow在1961年提出了他的高效编码假设[29],随后有人提出稀疏性可能是感知表示的基本原则[30]。其他研究表明,自然图像可以进行稀疏编码,这种编码特性与V1中的神经元细胞响应非常相似[31]。
许多人试图理解和解释稀疏性的潜在机制及其相关的生物学意义。为了帮助机器学习和智能算法的发展,人们从几个方面探索了稀疏性和稀疏编码的优势,包括但不限于编码能力、鲁棒性和泛化性、压缩感知和信息传输效率[1,27,32]。这些研究导致了字典学习算法[33]和新算法(如分层时间记忆(HTM)[32])的发展,这些算法利用稀疏性进行神经计算。
4.4.1 稀疏编码提高表示效率
稀疏编码的优势是什么?从学习角度来看,大脑对外部感知信息的表示和编码应该是一个提取“有效信息”的过程。为了解决这个问题,Ma等人[34]提出了简约原则[1]:一个智能系统试图从外部信息中提取低维信息,并将其组织成紧凑(即高效)和结构化的形式。提取的低维信息应遵循三个特征:可压缩性、线性和稀疏性。稀疏编码可以有效提高编码系统的表示能力。Ma等人使用量率减少来描述表示能力以说明这一点。使用稀疏字典学习[33]或独立成分分析等方法,稀疏编码下的特征可以保证尽可能正交,从而最大化不同特征的表示能力。
4.4.2 稀疏性有效提高机器学习模型的性能
稀疏性也应用于机器学习中。稀疏性可以用来对抗维度灾难[27]。理论上,对于单层感知器(单个神经元的简化模型)中的学习,只有当训练集的数量大于感知器中突触(即权重的数量)的数量时,才会出现较小的泛化误差[35]。这在复杂模型(如深度学习网络)中是不可接受的,因为参数的数量远大于样本的数量。Lage-Castellanos等人[36]发现,在单层感知器中引入L1正则化可以规避上述问题。因此,当将稀疏性作为先验知识添加到模型中时,可以提高机器学习模型的性能。
事实上,单个神经元比感知器复杂得多。通过模仿皮质锥体神经元的特性,Jeff Hawkins等人[32]开发了一种基于神经元稀疏分布的学习模型,即分层时间记忆(HTM),它具有分层突触结构和远端突触接收。这种结构似乎会影响层间信息的传输,因为远端突触不一定将神经排放传输到细胞质。然而,他们的研究表明,通过稀疏编码(即下层神经元的数量远大于激活神经元的数量),模型对输入噪声具有鲁棒性,同时确保匹配精度[32]。这种鲁棒性正是高维稀疏向量的特性。
4.4.3 稀疏性和压缩感知
自Tao等人[37,38]在2006年提出并发展了压缩感知理论以来,该理论在神经科学和人工智能中的应用也得到了广泛研究[26,27,39,40]。压缩感知理论指出,如果满足某些条件,高维中稀疏编码的信息可以通过低维通道传输而不会丢失信息。这在大脑中可能发挥重要作用,因为神经系统从外部世界接收的信号具有一定的稀疏性(自然图像、声音、气味等)。信息传输到更深大脑区域的效率和准确性是基本问题,压缩感知理论可能提供解决方案。例如,研究人员提出了一个在神经系统中可行的长程大脑通信理论模型[27,40],该模型可以在长程大脑传输中压缩高维信息,提高神经系统的信息传输效率。压缩感知理论还可以增强生物系统的工作记忆[39,41]。理论模型表明,神经电路可以记录长度超过其自身细胞数量的稀疏信号。相比之下,它们只能记录长度不超过神经元数量的信号。
4.5 结论:稀疏性和维度
正如Suryaz等人[27]指出的,“存储、通信和处理高维神经活动模式或外部刺激的问题对任何神经系统都提出了根本性挑战。”处理和学习外部信息是神经系统的基本任务。此外,高维信息通常在本质上具有稀疏性。稀疏编码策略可能是生物大脑处理外部信息所必需且可行的方法,并且可以提高这一过程的效率和鲁棒性。
第五章关系记忆:神经群体编码和流形
Bo Zhang, Jia Liu*
5.1 引言:关系记忆
知识存储是我们不可或缺的认知能力之一,一直是神经科学和计算科学的关键问题。关于大脑如何组织并将大量日常经验最终存储为知识的问题,最近的神经科学发现表明,大脑的记忆系统使用参照框架,通过该框架,不同信息的关系在中颞叶(MTL)中被精确形成。如今,参照框架的概念已经调和了海马体在非空间和空间记忆中的实验观察,并推动了一个新的有前景的研究方向:关系记忆。我们在这里提出参照框架作为神经元群体的第一个原则之一。
5.2 关于MTL功能的长期争论
MTL由海马体形成和几个解剖学上相邻的结构组成,包括内嗅皮层、旁海马皮层和内嗅皮层[1]。海马体是从患者研究中已知对记忆至关重要的最早区域。两个著名的研究案例是患者H.M.[2]和患者R.B.[3]。患者H.M.在无法控制的癫痫发作后接受了双侧中颞叶切除术。手术显著减少了癫痫发作的发生率和严重程度,而人格和一般智力没有明显变化。然而,意外观察到严重的短期记忆丧失。H.M.无法再识别医院工作人员,找到去洗手间的路,也无法回忆起他在医院日常生活中的事件。相比之下,他入院前的早期记忆仍然生动完整。与H.M.类似,患者R.B.在失忆后出现短期记忆障碍,但长期记忆和认知能力完好无损,组织学检查将他的记忆丧失限制在海马体CA1区的双侧损伤。这些20世纪60年代左右的记忆缺陷临床案例表明了短期记忆和长期记忆之间的区别,并强调了MTL在记忆巩固中的作用,即海马体的损伤导致学习经验无法从短期记忆转化为长期记忆。随着发展,短期和长期记忆都被归类为陈述性记忆,相关早期研究加深了我们对MTL功能的理解,并促进了经典记忆理论的构建[4]。然而,空间记忆作为另一类记忆,长期以来一直被该理论忽视。
对大脑空间编码理解的显著进展始于20世纪70年代,O'Keefe和他的同事[5]在老鼠的背侧海马体(CA1区)植入电极,并在老鼠在24 cm × 36 cm平台上对听觉、视觉、嗅觉和触觉刺激的行为过程中监测了总共八个单位的活性。结果显示,8个单位仅在老鼠位于平台特定位置时表现出响应。通过扩展观察[6]确认,从海马体CA1区记录的50个单位中有26个被分类为位置单位,这些单位在老鼠位于38 cm × 15 cm平台上的特定位置时表现出优先响应,选择性响应并非由于任何感官刺激、老鼠的行为或代表位置发生的任何动机因素,而是取决于其在平台上的位置。这些发现表明,海马体中的位置细胞提供了独立的位置代码。因此,可以通过位置细胞群体形成空间参照图,该图充当认知地图系统[7]。位置细胞的发现挑战了海马体的传统观点,并导致了一个对比的观点:海马体CA1区的细胞真的专门用于事件(非空间信息,例如医院工作人员的身份、去洗手间的路或日常经验)还是它们专门用于编码空间位置(空间信息,例如我站在房间门口附近)?尽管以Howard B. Eichenbaum为代表的研究人员开始提出海马体功能作为关系处理系统的桥梁框架[8],但陈述性记忆和空间记忆的研究主要并行进行,尽管两者都关注海马体功能(图1a)。
5.3 MTL系统的通用代码:参照框架
Moser和他的同事[9]在老鼠的背尾内侧内嗅皮层(dMEC)植入电极,目的是寻找海马体上游区域中位置细胞形成的类似地图结构组织的证据,他们记录了11只老鼠在方形盒子中收集散落的随机抛出的食物时的57个dMEC神经元。结果,记录的神经元的放电场中出现了显著的空间组织,放电场集中在正三角形网格的顶点上,这些正三角形网格规则地铺满了整个环境。他们将这些神经元命名为“网格细胞”。网格细胞的重复感受野最初被假设为基于路径整合的地图上编码动物的位置和运动方向。后来,它成为Constantinescu和她的同事[10]在陈述性记忆和空间记忆之间建立桥梁的线索。他们假设所谓的地图是由网格细胞概念上组织的,并测试人类在抽象而非物理空间中导航时是否使用类似网格的对称代码。在他们的实验[10]中,构建了一个概念上的2D“鸟空间”,鸟的颈长和腿长在连续维度上变化,每个鸟刺激与一个圣诞符号相关联。参与者在MRI扫描中通过按键根据颈长变化与腿长变化的比率对鸟进行变形,并在任务的广泛训练后。在这种情况下,比率根据鸟空间中的运动方向变化。设计的逻辑是,如果鸟空间信息由网格细胞编码,方向选择性(网格细胞轴的对齐或未对齐)将在参与者在不同方向移动后显示6倍调制。正如预期的那样,通过MEC的平均活动作为鸟空间中变形方向的函数揭示了稳定的网格状信号。
Constantinescu等人的发现作为一个里程碑,首次提供了网格细胞不仅编码物理空间还编码概念事件的证据(图1b)。继“鸟空间”之后,网格细胞的非空间编码通过各种类型的概念空间进一步得到证实,包括视觉[11]、气味[12]、奖励[13]和序列[14]空间。总的来说,这些研究支持了Eichenbaum提出的关系处理理论,即MTL展示了一种通用代码,将非空间知识组织成一个参照框架,知识可以通过全局关系方式存储或检索(例如,在鸟空间中,圣诞树与颈长且腿短的鸟相关联[10]),类似于在物理空间中组织空间关系。到目前为止,经验证据通过网格细胞研究的线索调和了空间和非空间记忆之间的区别,而网格细胞的发现依赖于位置细胞的研究。2014年,诺贝尔生理学或医学奖授予John O’Keefe、May-Britt Moser和Edvard I. Moser,以表彰他们发现编码大脑空间坐标系统的位置细胞和网格细胞。更重要的是,这些细胞提供了关于外部世界的日常经验如何通过与记忆类别无关的参照框架组织的显著见解[15]。
MTL统一框架的首次成功实现最近由Whittington和他的同事在2020年[16]完成,他们构建了一个名为Tolman-Eichenbaum机器(TEM)的参照框架系统。基于不同方面的知识分别表示并可以灵活重组以表示新经验的假设,TEM机器使用“因式分解和结合”方法进行知识的结构泛化,以便可以学习和预测在空间和非空间记忆任务中观察到的大范围神经表示。具体来说,任务要求TEM在由一组节点组成的2D图上移动,每个节点与一个感官观察(例如,香蕉的图像)相关联,通过生成模型训练的TEM机器能够预测下一个感官观察并成功泛化结构知识。结果,通过TEM的性能和成功复制生物观察(包括位置细胞和网格细胞的出现以及重映射现象)证明了使用关系知识模拟MTL功能的效率。
5.4 使用参照框架的知识存储和检索的群体编码
理论上,参照框架可以以连续和定量的方式尽可能多地存储知识,以对应于特定特征[18]。不可避免地,单个维度的参照框架将无法存储由多特征构成的知识,这已被强调为两种灵活记忆表达形式的基础[17],“传递性”表示判断共享共同特征的知识对的能力(例如,A > B & B > C,则A > C),以及“对称性”表示将知识对按事件顺序的反向关联的能力(例如,B到C,则C到B)。为了满足多样性的需求,必须要求群体编码从多个维度链接知识片段,这依赖于数十万个参照框架[18]。最近,来自神经科学和计算科学的研究集中在神经元放电率的拓扑结构上,他们的结果显示了证据,表明神经元群体协调嵌入在参照框架中的知识(即知识存储)并在复杂环境中辅助导航(即知识检索)。鉴于群体编码的动态性,这些研究为揭示神经元如何高效地相互作用以存储和检索关系记忆的原则指明了方向,这是一个经典问题,几十年来一直有待解答。
神经元相互作用机制的研究最初来自计算建模领域,如Amari提出的竞争-合作机制[19],该机制假设形成一系列吸引子的周期性权重函数[另见第1章吸引子网络]。在空间导航场景中,每个吸引子都以二维欧几里得空间中的一个位置为中心,神经相互作用由周期性函数的兴奋(正)或抑制(负)权重决定。吸引子网络,特别是其变体之一称为“连续吸引子神经网络”(CANN),成功模拟了位置细胞[20]和网格细胞[21,22]的模式动态,从而空间知识可以被细胞稳定编码。在CANNs的基础上,Samsonovich和McNaughton[20]进一步提出,网格细胞群体的放电率依赖于称为“环面”的拓扑结构(图1c)。与运动最终会被限制的欧几里得空间不同,环面结构没有边界以适应网格细胞的周期性模式,因此从环面上任何位置开始的运动永远不会被限制,但最终会回到原点。最近,Moser和他的同事提供了第一个生理学证据,证明了这种环面结构的存在[23]。在他们的实验中,当老鼠进行觅食行为或睡眠时,通过高密度Neuropixels硅探针同时记录了数百个网格细胞。在对单个尺度内的149个网格细胞的放电率进行降维处理并将主成分转换为3D可视化后,清晰地揭示了一个环面状结构,并且在动物的认知状态(即清醒或睡眠)中保持稳定。在环面结构中,网格细胞群体作为一个整体组织,环面的内圈和外圈分别对应于欧几里得空间的水平轴和垂直轴。因此,环面上的每个位置代表一个具有唯一相位对(分别对应于内圈和外圈)的网格细胞,在给定的空间模块下无缝编码物理空间。鉴于拓扑形态,假设数十万个参照框架由欧几里得空间之外的高维拓扑空间灵活组织的假设因此直接得到证明。
从动态角度来看,环面结构表面的运动对应于一系列知识检索的过程。然而,每个运动决定下一个“位置”(例如,A到B然后B到C)的原则是什么?受网格细胞的生理学证据启发,发现模块大小(场大小的间距)的梯度沿着dMEC的背侧到腹侧部分,并且网格细胞的相位随机分布,提出了大脑的模块化系统[9,24]。该系统说明了相位和位置之间的映射关系,从而动物的位置可以通过一组相位唯一指定,
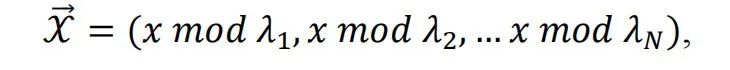

支持这一算法的证据最近由O’Keefe和他的同事[28]发现。在他们的实验中,当老鼠在蜂窝迷宫中导航到目标以获取食物奖励时,记录了5只老鼠的456个CA1位置细胞。令人惊讶的是,456个细胞中的142个细胞的放电模式显示出向目标附近位置收敛的矢量场。当将细胞的矢量场相加时,当动物朝向目标时,可以从群体矢量图中清晰地看到最大放电率(称为“收敛汇”)(图1c)。此外,矢量场灵活地适应目标位置,即当原始目标位置移动时,群体编码的最大放电率重新组织到新目标。这些结果直接支持了赢家通吃机制,即ERC-HPC系统创建了一个基于矢量的模型来支持灵活导航。
随着对基于矢量导航的神经元群体编码的最新理解,机器学习领域的神经网络在基于大脑启发的识别记忆[26]和空间导航[27]应用中取得了巨大成功。Bicanski和Burgess开发了一个视觉记忆模型,使用网格细胞群体驱动扫视,从而可以识别熟悉的面孔、物体和场景[26]。在模型的导航部分,图像上每个注视位置由100个网格细胞在注视位置的九个空间尺度的独特放电率矢量表示。给定当前和随机目标位置,可以使用赢家通吃机制计算决定扫视的位移矢量。最终,通过在图像特征(例如,给定面孔的鼻子)和位置细胞(称为特征标签细胞)、位置细胞和网格细胞以及网格细胞和位移矢量之间建立权重关系,成功模拟了海马体形成导航功能,以指导眼动。在Banino的研究[27]中,一个递归网络被训练在2.2 m × 2.2 m的方形竞技场中执行基于矢量的导航。结果,网络表现得像哺乳动物一样准确,暗示了网格细胞群体在编码非空间和空间知识方面的巨大能力。
5.5 结论:参照框架系统
通过回顾关系记忆的最新发现,我们主张未来的研究应更多关注大脑的参照框架系统。尽管参照框架的某些方面,如群体编码的作用,已经揭示,但仍需要更多工作来全面理解参照框架的本质,例如,参照框架的多样性、可塑性或脑区依赖的功能。此外,据我们所知,参照框架的研究也将有助于促进基于大脑启发的发现向AI研究的转化,至少在以下两个方向上。一是图论的发展,参照框架可能用于解决子图同构问题,而赢家通吃机制可能有助于解释路由问题。更重要的是,群体编码将有助于基于生物学的节点和边概念的理解。另一个是认知推理和判断,通过这些过程,我们的大脑不仅检索存储的知识(即判别模型),还生成超越经验的新知识(即生成模型)。例如,我们可以使用“想象力”能力反复模拟未来计划,直到找到最优解决方案。总之,未来对参照框架的研究将有助于灵活的知识安排,这是揭示关系记忆机制和开发AI通用知识编码框架的关键。
第六章神经可塑性:知觉学习的教训
Luyao Chen, Xizi Gong, Fang Fang*
6.1 引言:感知学习和可塑性
大脑是一个涉及几乎所有生命活动的庞大有序动态神经网络系统。经验可以在这个神经网络系统中引起神经元和神经回路功能特性的变化,这被称为大脑可塑性,有助于个体适应环境。感知学习是感知系统适应外部环境的典型现象,指的是通过反复练习或经验对物理刺激的感知产生持续和牢固的变化[1,2,3]。它表现为在数月和数年内逐渐无意识地提高识别感知特征和物体的能力[4]。这种感知能力的提高伴随着大脑多个结构和功能水平上的神经变化,从而为研究大脑可塑性提供了极好的范式。
6.2 感知学习的特异性和迁移
6.2.1 现象学
传统观点认为,感知系统在个体发展的早期阶段具有高度可塑性。然而,这并不意味着成年个体的脑功能是固化的。感知学习,即通过练习产生的长期性能改善,已被广泛用作研究成年个体经验依赖性大脑可塑性的范式[1,2,3]。感知学习是感知系统适应外部环境的典型现象。它指的是通过练习或经验对某些刺激的感知产生更持续和牢固的变化。与一般意义上的学习不同,感知学习不获取显性知识,而是与隐性记忆相关,表现为辨别或识别感知特征和物体能力的提高。感知学习可以发生在多种感觉模式中,如视觉、听觉、嗅觉、触觉和味觉。在本章中,我们的回顾主要集中在视觉感知学习上。
感知学习的特异性和迁移被定义为第二个任务的性能是否显示改善。在早期研究中,视觉感知学习的特异性通过将获得的行为改善与训练刺激和任务的物理特性相结合来证明。这意味着感知学习可能发生在低级皮质区域。学习中使用的感官信息源自早期视网膜定位视觉区域,具有较小的感受野[5]。“早期”理论将感知学习效应归因于初级视觉皮质中神经元调谐的变化[6,7]。Dosher和Lu根据涉及的部位或皮质水平将特异性分为五类:视网膜位置、训练眼、刺激特征或物体、判断性质和测试上下文[8]。对于每个类别,部分特异性和部分迁移是常见的模式,在不同的观察任务中积累了证据。以标志性的视网膜位置特异性为例,Schoups等人精确评估了方向辨别任务中的视网膜位置特异性[9]。参与者首先在中央凹练习,然后在5°环周围的一系列外周位置练习。结果表明,学习改善特定于外周位置。由于在不同外周位置的预训练性能优于中央凹,因此可以得出结论,迁移从中央凹到外周位置。
另一方面,一系列研究表明,感知学习的特异性可以减少甚至完全消除[10,11,12,13,14]。例如,通过在第一个位置进行对比训练和在第二个位置进行方向训练的双重训练范式,Xiao等人展示了对比到第二个位置的完全迁移[11]。这种感知学习的迁移表明,学习过程可能还涉及高级皮质,以便为不同刺激进行更复杂的处理参与者。在下一部分中,我们将回顾单神经元和fMRI研究,揭示学习相关变化在大脑多个阶段发生,从而调和感知学习的特异性和迁移之间的冲突。
6.2.2 感知学习的神经机制
对应于感知学习的特异性,大量电生理和fMRI研究表明,感知学习与早期视觉皮质区域活动的增强相关。2001年,Schoups对猕猴的研究将训练神经元的神经性能改善与行为改善在方向识别中联系起来[7]。观察到训练神经元的调谐曲线斜率有特定且高效的增加,这些神经元最有可能编码识别的方向。同时,未训练方向的调谐曲线没有变化。2010年,Hua等人结合行为评估和猫的体外单神经元记录,研究了方向识别任务中的训练效果[15]。结果显示,猫对光栅的感知对比敏感度通过训练显著提高,训练眼的效果更为显著。对于V1中的单神经元记录结果,训练猫的神经元平均对比敏感度显著高于未训练猫。他们的结果表明,训练诱导的V1神经元对比增益揭示了感知对比敏感度的行为改善。为了检查人类视觉皮质在感知学习过程中的激活变化,Yotsumoto等人使用fMRI研究中的纹理辨别任务(TDT)[16]。结果表明,V1中相应的BOLD激活随着参与者的行为表现增加,而当表现饱和时减少。此外,人类EEG实验的证据显示,当训练改善行为表现时,早期视觉皮质的C1成分迅速上升[17]。这表明,感知学习导致的早期视觉区域反应增加源于局部感受野的变化,而不是来自后期视觉区域的反馈。此外,一项应用神经反馈技术的MRI研究通过去除外部视觉输入并仅依赖视觉皮质的训练神经信号来改善行为表现,支持了初级视觉皮质在感知学习中起决定性作用的观点[18]。2016年,Yu等人使用特定眼和视觉半视野的对比检测任务进行了30天的训练,以研究皮下核的感知学习[19]。结果显示,外侧膝状核(LGN)的fMRI信号对低对比度模式增加。增加特定于训练眼和视觉半视野,仅发生在大细胞层,而在小细胞层中不存在,即使受试者不注意模式。这些发现表明,感知学习诱导的神经可塑性可能早在丘脑水平就发生。
然而,也有研究表明,与注意和决策相关的大脑区域与感知学习相关[2,20,21,22]。具体来说,感知学习与顶内沟(IPS)、外侧顶叶(LIP)和前扣带回(ACC)等前顶叶区域的选择性增强或神经反应减弱相关[23,24,25]。此外,反向层次理论声称,是自上而下而不是自下而上的信息流主导了学习过程[26]。学习首先发生在任务特定的高级层,然后在必要时在低级层实现。这一理论在一定程度上解释了感知学习中迁移的发生。同时,一些研究也表明,感知学习与视觉和决策区域之间功能连接的增加相关[27,28]。重新加权理论认为,感知学习并不改变早期视觉皮质的功能特性;相反,它改变了代表视觉信息的神经元与决策单元之间连接的强度(权重)[29]。基于重新加权理论,Law和Gold将学习建模为高级决策神经元对其与特定训练运动方向的感觉神经元连接权重的精炼过程[24,25,26,27,28]。一项关于运动辨别感知学习的研究表明,行为改善可以通过V3A中刺激的感觉表示变化以及V3A到IPS的连接变化来解释[27]。同样,为了研究感知学习如何调节人类大脑中与决策相关区域的活动,采用了一种基于模型的方法,使用运动方向辨别任务[30]。除了前顶叶网络和决策网络中神经反应的增强外,结果还显示V3A到腹侧前运动皮质(PMv)和IPS到额叶眼区(FEF)的连接增强与训练并行。总之,感知学习的机制不是一个简单的过程,而是多个大脑区域之间的复杂交互,因此在不同条件下可以观察到特异性和迁移。
6.2.3 GABA在感知学习中的作用
GABA是一种参与大脑神经元抑制调节的分子。先前的动物研究表明,GABA能抑制在学习和中突触可塑性中起重要作用[31,32]。此外,人类MRS研究表明,视觉皮质中的GABA浓度与稳态可塑性相关[33],而运动皮质中的GABA浓度与个体能力[34,35]和运动学习中的表现改善[36,37,38]相关。具体来说,在视觉感知学习中,GABA水平对两个视觉任务表现改善的影响显示出相反的方向[39]。在目标检测任务中,受试者在训练后GABA减少时表现更好,而在特征辨别任务中,受试者在训练后GABA增加时表现更好。来自药理学操作的证据也突显了GABA在学习中的重要作用。通过长期使用选择性5-羟色胺再摄取抑制剂(SSRI)氟西汀,成年大鼠的视觉皮质可塑性可以增强,而如果使用地西泮增加GABA,增强效果将被阻断[40]。
6.3 Hebbian规则和感知学习的计算模型
1949年,Hebb提出:“当A细胞的轴突足够接近以激发B细胞并反复或持续参与激发它时,一个或两个细胞中会发生某种生长过程或代谢变化,使得A作为激发B的细胞之一的效率增加”[41]。高频间歇刺激诱导的长时程增强(LTP)和低频间歇刺激诱导的长时程抑制(LTD)共同允许双向突触修饰,并被认为是学习和记忆的突触基础[42,43,44]。进一步,脉冲时间依赖性可塑性(STDP)表明,突触修饰的方向取决于突触前和突触后脉冲的时间顺序[45,46,47,48,49]。具体来说,反复暴露于





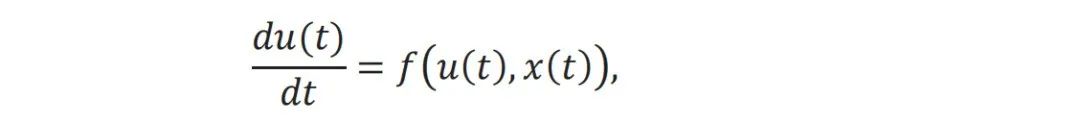


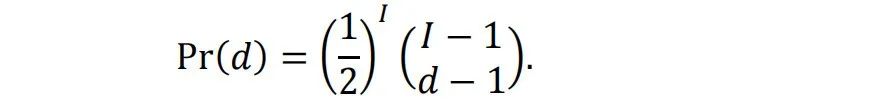
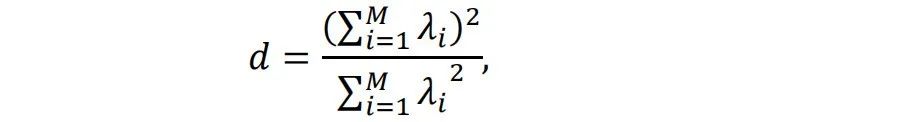
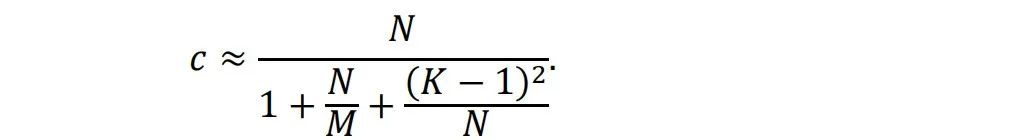
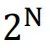 个项目,显著提高了表示能力。即使对于一个项目,只有少数(最多K个)神经元可能同时激活,如稀疏编码的情况,不同代码的总数也将是
个项目,显著提高了表示能力。即使对于一个项目,只有少数(最多K个)神经元可能同时激活,如稀疏编码的情况,不同代码的总数也将是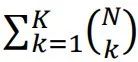 。与局部编码相比,这种配置节省了神经元,并以更少的能量编码相同的信息。然而,分布式代码的读出不简单,并且以生物学上合理的方式学习可能具有挑战性。相比之下,局部代码及其输出的关联可以通过简单的Hebbian机制建立;因此,如果神经活动模式是稀疏编码的,学习将更加高效[3, 6]。
。与局部编码相比,这种配置节省了神经元,并以更少的能量编码相同的信息。然而,分布式代码的读出不简单,并且以生物学上合理的方式学习可能具有挑战性。相比之下,局部代码及其输出的关联可以通过简单的Hebbian机制建立;因此,如果神经活动模式是稀疏编码的,学习将更加高效[3, 6]。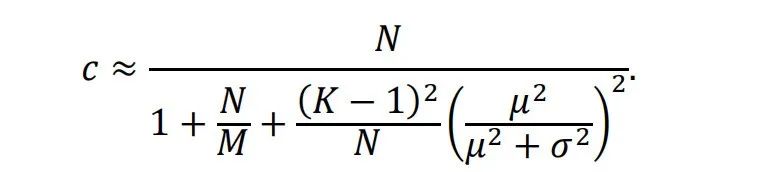


 鲁公网安备37020202000738号
鲁公网安备37020202000738号