推荐学习
- 刷透近200道数据结构与算法,成功加冕“题王”,挤进梦中的字节
- 牛掰!“基础-中级-高级”Java程序员面试集结,看完献出我的膝盖
01 前言
学习算法,我们不需要死记硬背那些冗长复杂的背景知识、底层原理、指令语法……需要做的是领悟算法思想、理解算法对内存空间和性能的影响,以及开动脑筋去寻求解决问题的最佳方案。相比编程领域的其他技术,算法更纯粹,更接近数学,也更具有趣味性。
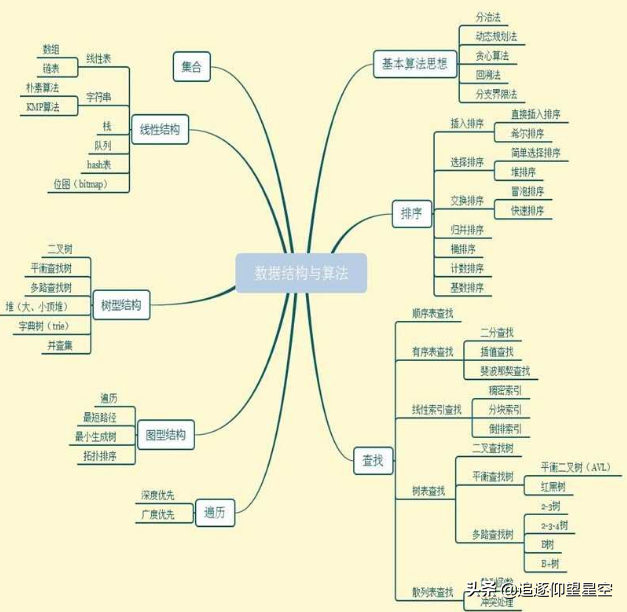
本文将回顾数据结构与算法的基础知识,学习日常所接触场景中的一些算法和策略,以及这些算法的原理和他背后的思想,最后会动手写代码,用java里的数据结构来实现这些算法,如何去做?
02 基本概念回顾
2.1 什么是数据结构?
1)概述
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。
2)划分
从关注的维度看,数据结构可以划分为数据的逻辑结构和物理结构,同一逻辑结构可以对应不同的存储结构。逻辑结构反映的是数据元素之间的逻辑关系,逻辑关系是指数据元素之间的前后间以什么形式相互关联,这与他们在计算机中的存储位置无关。逻辑结构包括:
集合:只是扎堆凑在一起,没有互相之间的关联
线性结构:一对一关联,队形
树形结构:一对多关联,树形
图形结构:多对多关联,网状
数据物理结构指的是逻辑结构在计算机存储空间中的存放形式(也称为存储结构)。一般来说,一种数据结构的逻辑结构根据需要可以表示成多种存储结构,常用的存储结构有顺序存储、链式存储、索引存储和哈希存储等。
顺序存储:用一组地址连续的存储单元依次存储集合的各个数据元素,可随机存取,但增删需要大批移动
链式存储:不要求连续,每个节点都由数据域和指针域组成,占据额外空间,增删快,查找慢需要遍历
索引存储:除建立存储结点信息外,还建立附加的索引表来标识结点的地址。检索快,空间占用大
哈希存储:将数据元素的存储位置与关键码之间建立确定对应关系,检索快,存在映射函数碰撞问题
3)程序中常见的数据结构
数组(Array):连续存储,线性结构,可根据偏移量随机读取,扩容困难
栈( Stack):线性存储,只允许一端操作,先进后出,类似水桶
队列(Queue):类似栈,可以双端操作。先进先出,类似水管
链表( LinkedList):链式存储,配备前后节点的指针,可以是双向的
树( Tree):典型的非线性结构,从唯一的根节点开始,子节点单向执行前驱(父节点)
图(Graph):另一种非线性结构,由节点和关系组成,没有根的概念,互相之间存在关联
堆(Heap):特殊的树,特点是根结点的值是所有结点中最小的或者最大的,且子树也是堆
散列表(Hash):源自于散列函数,将值做一个函数式映射,映射的输出作为存储的地址
2.2 什么是算法
算法指的是基于存储结构下,对数据如何有效的操作,采用什么方式可以更有效的处理数据,提高数据运算效率。数据的运算是定义在数据的逻辑结构上,但运算的具体实现要在存储结构上进行。一般涉及的操作有以下几种:
检索:在数据结构里查找满足一定条件的节点。
插入:往数据结构中增加新的节点,一般有一点位置上的要求。
删除:把指定的结点从数据结构中去掉,本身可能隐含有检索的需求。
更新:改变指定节点的一个或多个字段的值,同样隐含检索。
排序:把节点里的数据,按某种指定的顺序重新排列,例如递增或递减。
03 数据结构基础
3.1 数组
数组对应的英文是array,是有限个相同类型的变量所组成的有序集合,数组中的每一个变量被称为元素。数组是最为简单、最为常用的数据结构。
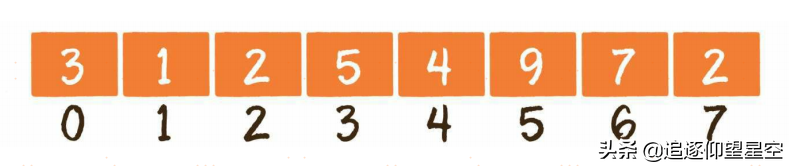
数组的另一个特点,是在内存中顺序存储,因此可以很好地实现逻辑上的顺序表。
内存是由一个个连续的内存单元组成的,每一个内存单元都有自己的地址。在这些内存单元中,有些被其他数据占用了,有些是空闲的。
数组中的每一个元素,都存储在小小的内存单元中,并且元素之间紧密排列,既不能打乱元素的存储顺序,也不能跳过某个存储单元进行存储。

3.2 链表
链表(linked list)是一种在物理上非连续、非顺序的数据结构,由若干节点(node)所组成。
单向链表的每一个节点又包含两部分,一部分是存放数据的变量data,另一部分是指向下一个节点的指针next。

双向链表比单向链表稍微复杂一些,它的每一个节点除了拥有data和next指针,还拥有指向前置节点的prev指针。

如果说数组在内存中的存储方式是顺序存储,那么链表在内存中的存储方式则是随机存储。
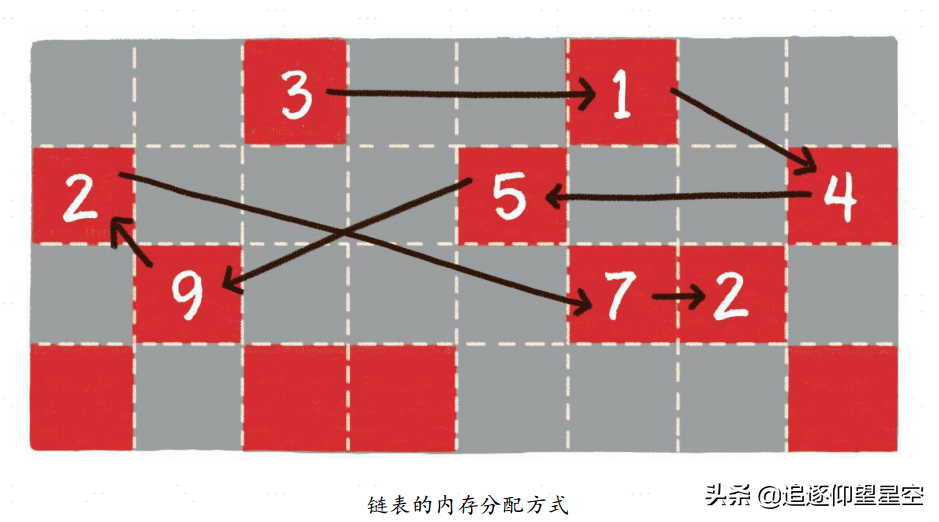
3.3 栈和队列
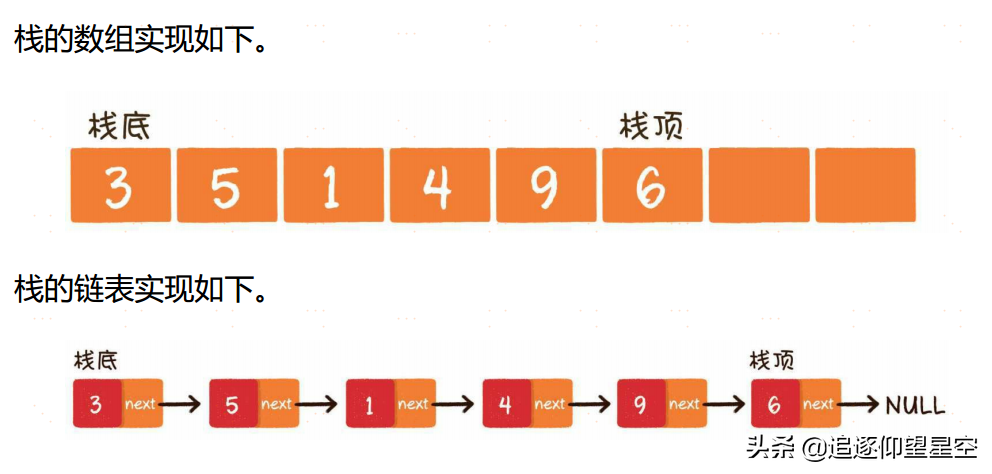
栈(stack)是一种线性数据结构,它就像一个上图所示的放入乒乓球的圆筒容器,栈中的元素只能先入后出(First In Last Out,简称FILO)。最早进入的元素存放的位置叫作栈底(bottom),最后进入的元素存放的位置叫作栈顶(top)。
栈这种数据结构既可以用数组来实现,也可以用链表来实现。
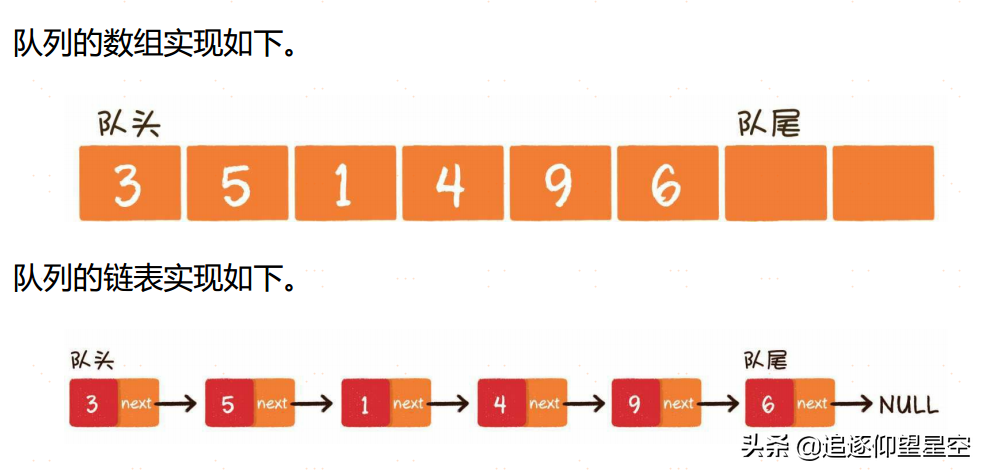
队列(queue)是一种线性数据结构,它的特征和行驶车辆的单行隧道很相似。不同于栈的先入后出,队列中的元素只能先入先出(First In First Out,简称FIFO)。队列的出口端叫作队头(front),队列的入口端叫作队尾(rear)。
3.4 散列表
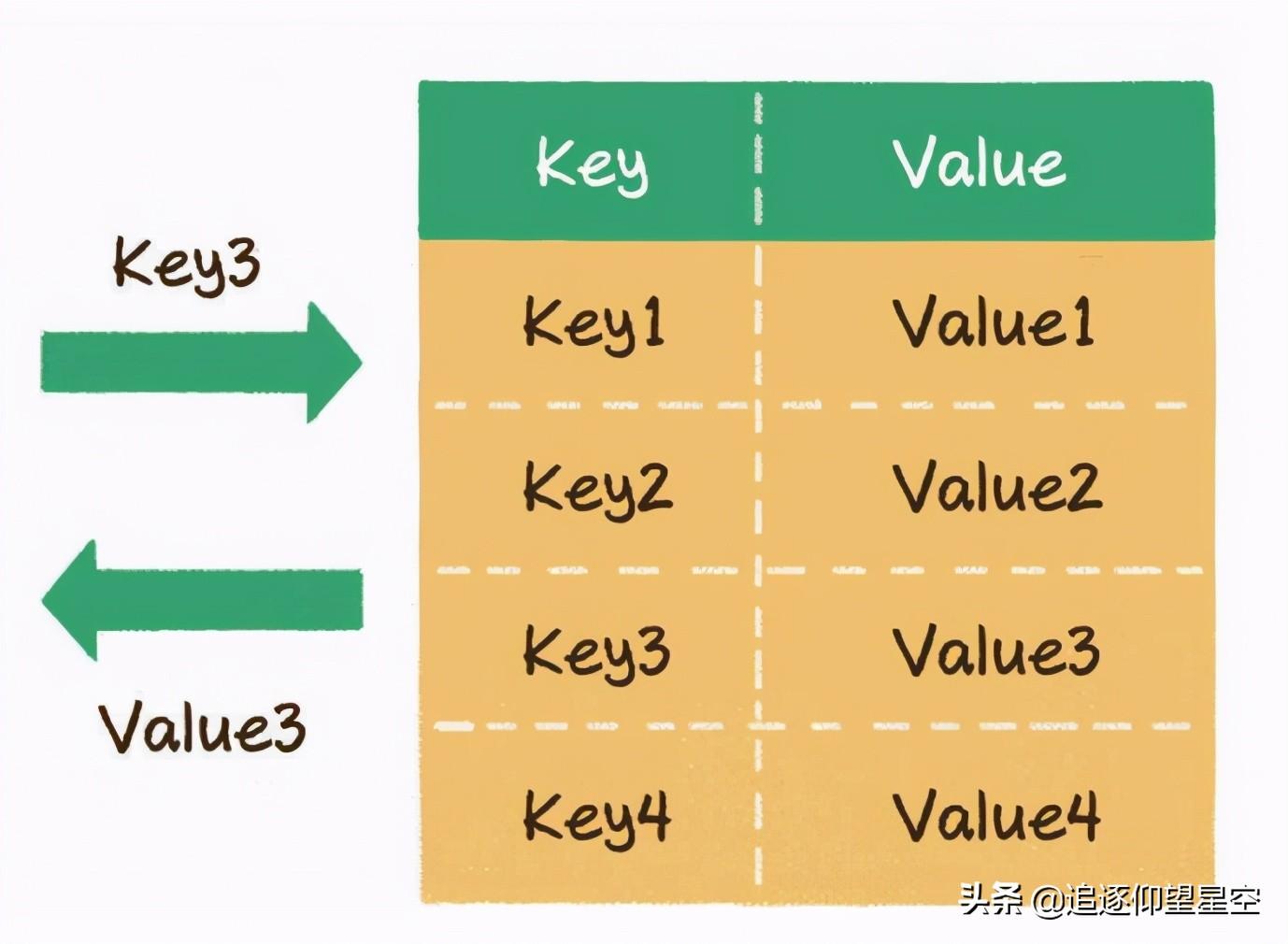
散列表也叫作哈希表(hash table),这种数据结构提供了键(Key)和值(Value)的映射关系。只要给出一个Key,就可以高效查找到它所匹配的Value,时间复杂度接近于O(1)。
由于数组的长度是有限的,当插入的Entry越来越多时,不同的Key通过哈希函数获得的下标有可能是相同的。这种情况,就叫作哈希冲突。
解决哈希冲突的方法主要有两种,一种是开放寻址法,一种是链表法。
开放寻址法的原理很简单,当一个Key通过哈希函数获得对应的数组下标已被占用时,我们可以“另谋高就”,寻找下一个空档位置。
这就是开放寻址法的基本思路。当然,在遇到哈希冲突时,寻址方式有很多种,并不一定只是简单地寻找当前元素的后一个元素,这里只是举一个简单的示例而已。在Java中,ThreadLocal所使用的就是开放寻址法。
接下来,重点讲一下解决哈希冲突的另一种方法——链表法。这种方法被应用在了Java的集合类HashMap当中。
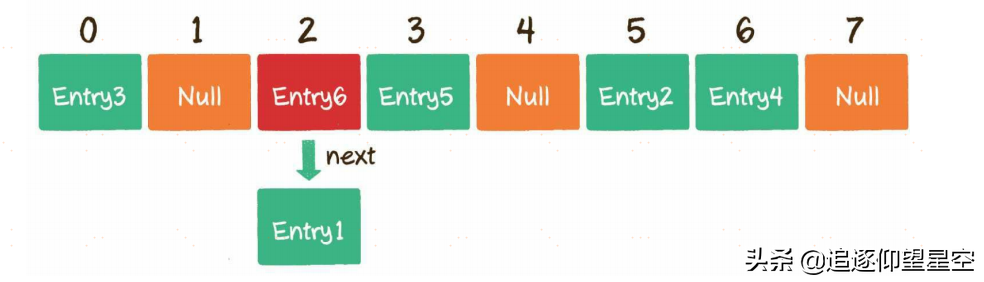
HashMap数组的每一个元素不仅是一个Entry对象,还是一个链表的头节点。每一个Entry对象通过next指针指向它的下一个Entry节点。当新来的Entry映射到与之冲突的数组位置时,只需要插入到对应的链表中即可。
3.5 树
树和图就是典型的非线性数据结构,我们首先讲一讲树的知识。
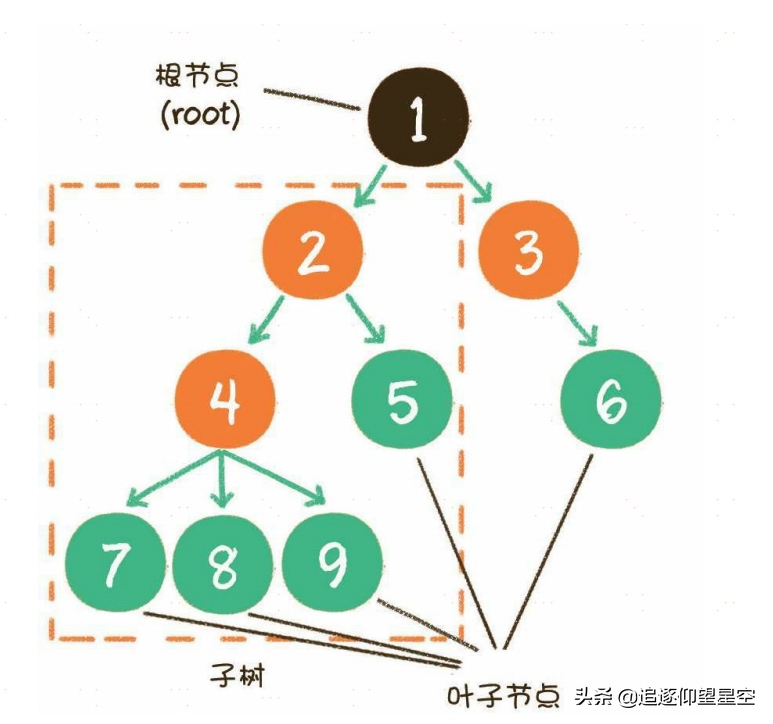
树(tree)是n(n≥0)个节点的有限集。当n=0时,称为空树。在任意一个非空树中,有如下特点。
- 有且仅有一个特定的称为根的节点。
- 当n>1时,其余节点可分为m(m>0)个互不相交的有限集,每一个集合本身又是一个树,并称为根的子树。
二叉树
二叉树(binary tree)是树的一种特殊形式。二叉,顾名思义,这种树的每个节点最多有2个孩子节点。注意,这里是最多有2个,也可能只有1个,或者没有孩子节点。
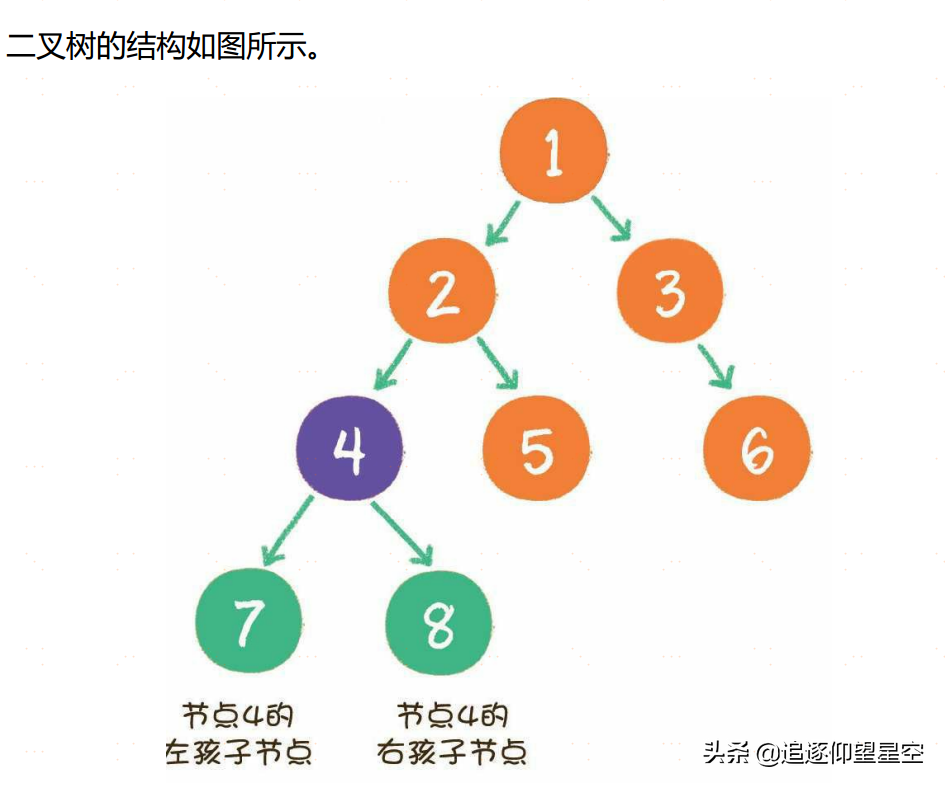
二叉树节点的两个孩子节点,一个被称为左孩子(left chi ld),一个被称为右孩子(right chi ld)。这两个孩子节点的顺序是固定的,就像人的左手就是左手,右手就是右手,不能够颠倒或混淆。此外,二叉树还有两种特殊形式,一个叫作满二叉树,另一个叫作完全二叉树。
二叉树存储结构
- 链式存储结构。
- 数组。
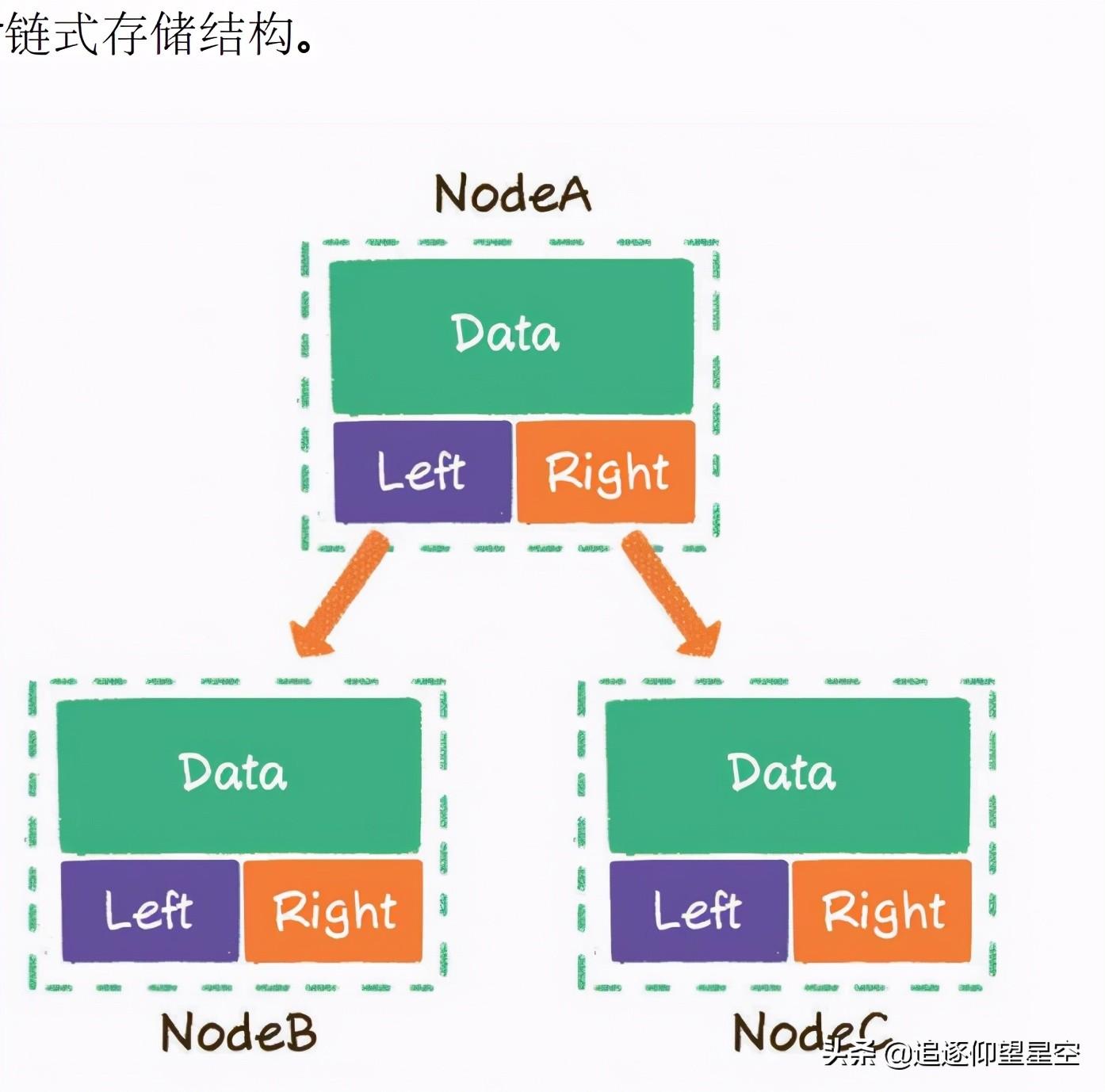
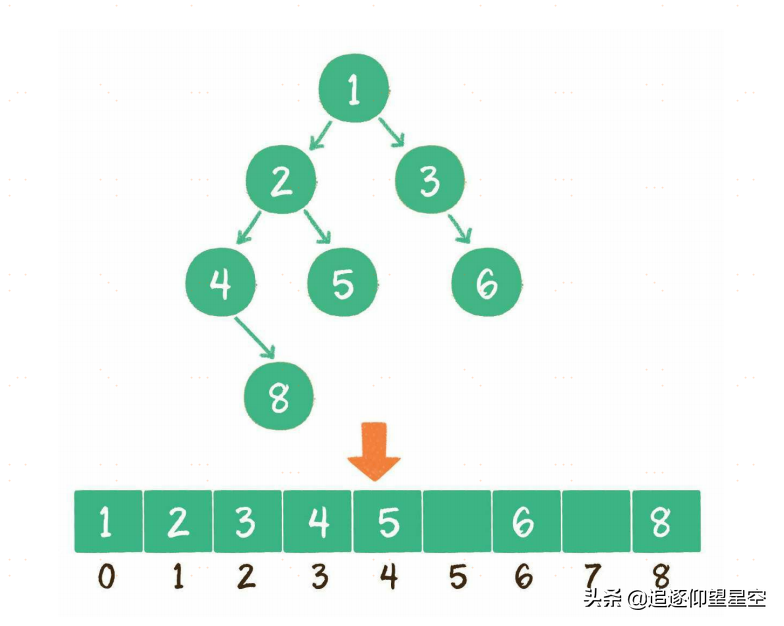
3.6 小结
什么是数组?
数组是由有限个相同类型的变量所组成的有序集合,它的物理存储方式是顺序存储,访问方式是随机访问。利用下标查找数组元素的时间复杂度是O(1),中间插入、删除数组元素的时间复杂度是O(n)。
什么是链表?
链表是一种链式数据结构,由若干节点组成,每个节点包含指向下一节点的指针。链表的物理存储方式是随机存储,访问方式是顺序访问。查找链表节点的时间复杂度是O(n),中间插入、删除节点的时间复杂度是O(1)。
什么是栈?
栈是一种线性逻辑结构,可以用数组实现,也可以用链表实现。栈包含入栈和出栈操作,遵循先入后出的原则(FILO)。
什么是队列?
队列也是一种线性逻辑结构,可以用数组实现,也可以用链表实现。队列包含入队和出队操作,遵循先入先出的原则(FIFO)。
什么是散列表?
散列表也叫哈希表,是存储Key-Value映射的集合。对于某一个Key,散列表可以在接近O(1)的时间内进行读写操作。散列表通过哈希函数实现Key和数组下标的转换,通过开放寻址法和链表法来解决哈希冲突。
什么是树?
树是n个节点的有限集,有且仅有一个特定的称为根的节点。当n>1时,其余节点可分为m个互不相交的有限集,每一个集合本身又是一个树,并称为根的子树。
什么是二叉树?
二叉树是树的一种特殊形式,每一个节点最多有两个孩子节点。二叉树包含完全二叉树和满二叉树两种特殊形式。
二叉树的遍历方式有几种?
根据遍历节点之间的关系,可以分为前序遍历、中序遍历、后序遍历、层序遍历这4种方式;从更宏观的角度划分,可以划分为深度优先遍历和广度优先遍历两大类。
什么是二叉堆?
二叉堆是一种特殊的完全二叉树,分为最大堆和最小堆。
在最大堆中,任何一个父节点的值,都大于或等于它左、右孩子节点的值。
在最小堆中,任何一个父节点的值,都小于或等于它左、右孩子节点的值。
什么是优先队列?
优先队列分为最大优先队列和最小优先队列。
在最大优先队列中,无论入队顺序如何,当前最大的元素都会优先出队,这是基于最大堆实现的。
在最小优先队列中,无论入队顺序如何,当前最小的元素都会优先出队,这是基于最小堆实现的。
04 排序算法
4.1 冒泡排序
冒泡排序的英文是bubble sort,它是一种基础的交换排序。

按照冒泡排序的思想,我们要把相邻的元素两两比较,当一个元素大于右侧相邻元素时,交换它们的位置;当一个元素小于或等于右侧相邻元素时,位置不变。
排序过程如下

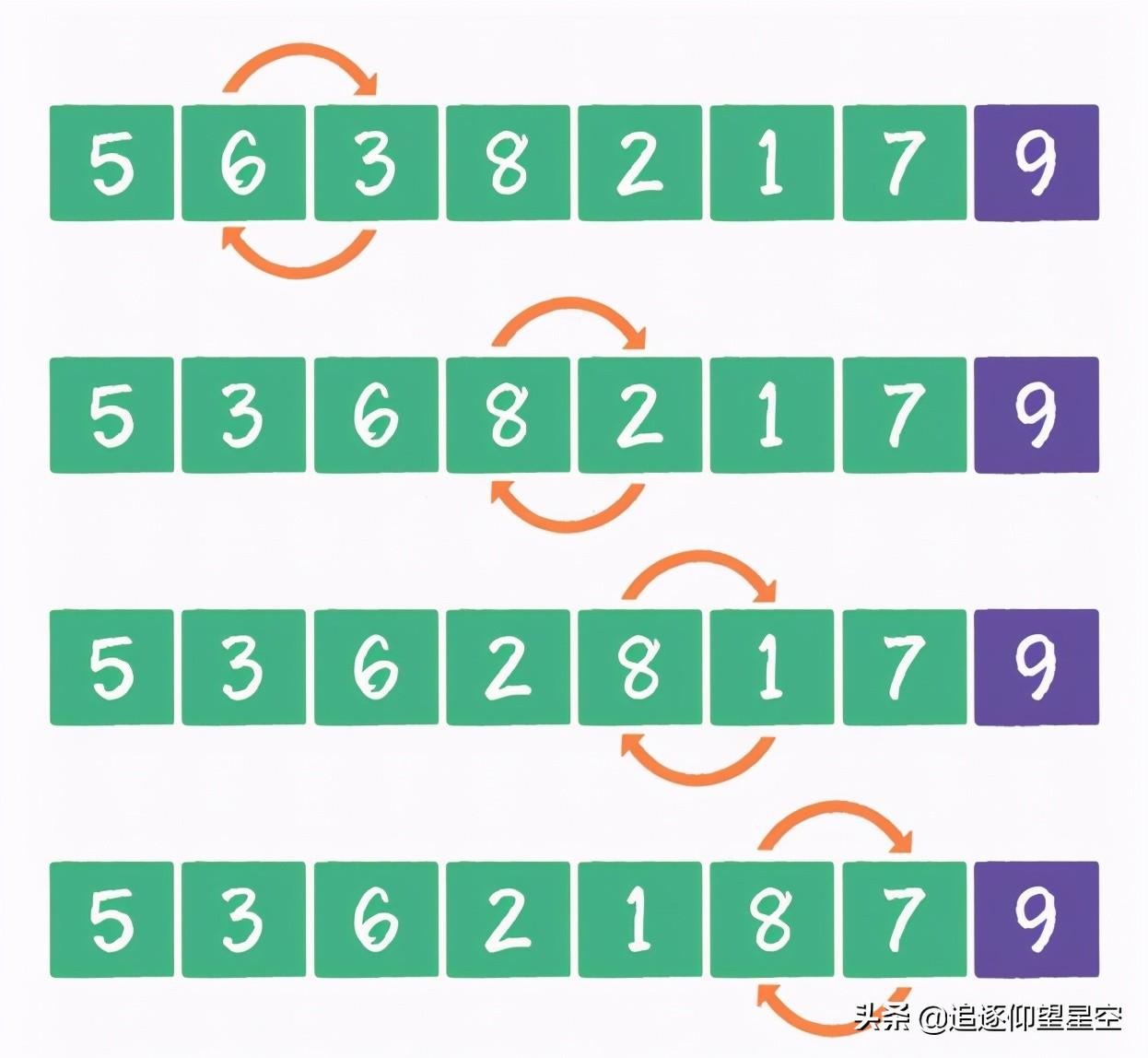
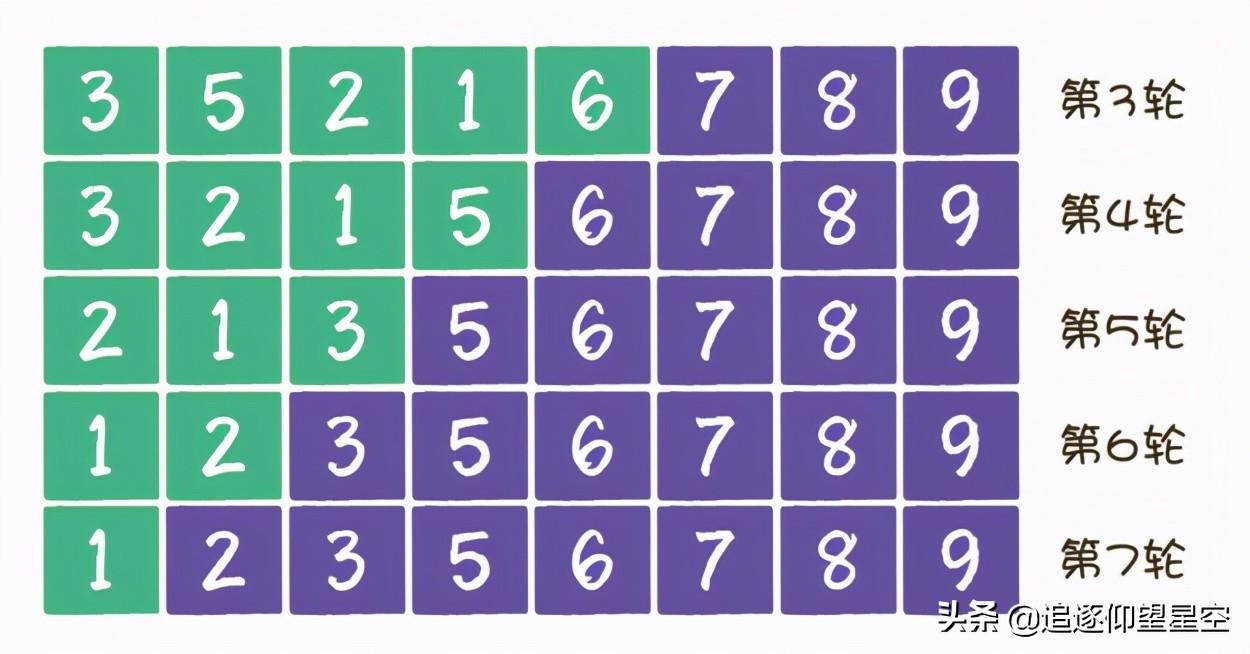
到此为止,所有元素都是有序的了,这就是冒泡排序的整体思路。
冒泡排序是一种稳定排序,值相等的元素并不会打乱原本的顺序。由于该排序算法的每一轮都要遍历所有元素,总共遍历(元素数量-1)轮,所以平均时间复杂度是O(n2)。
4.2 快速排序
同冒泡排序一样,快速排序也属于交换排序,通过元素之间的比较和交换位置来达到排序的目的。
不同的是,冒泡排序在每一轮中只把1个元素冒泡到数列的一端,而快速排序则在每一轮挑选一个基准元素,并让其他比它大的元素移动到数列一边,比它小的元素移动到数列的另一边,从而把数列拆解成两个部分。
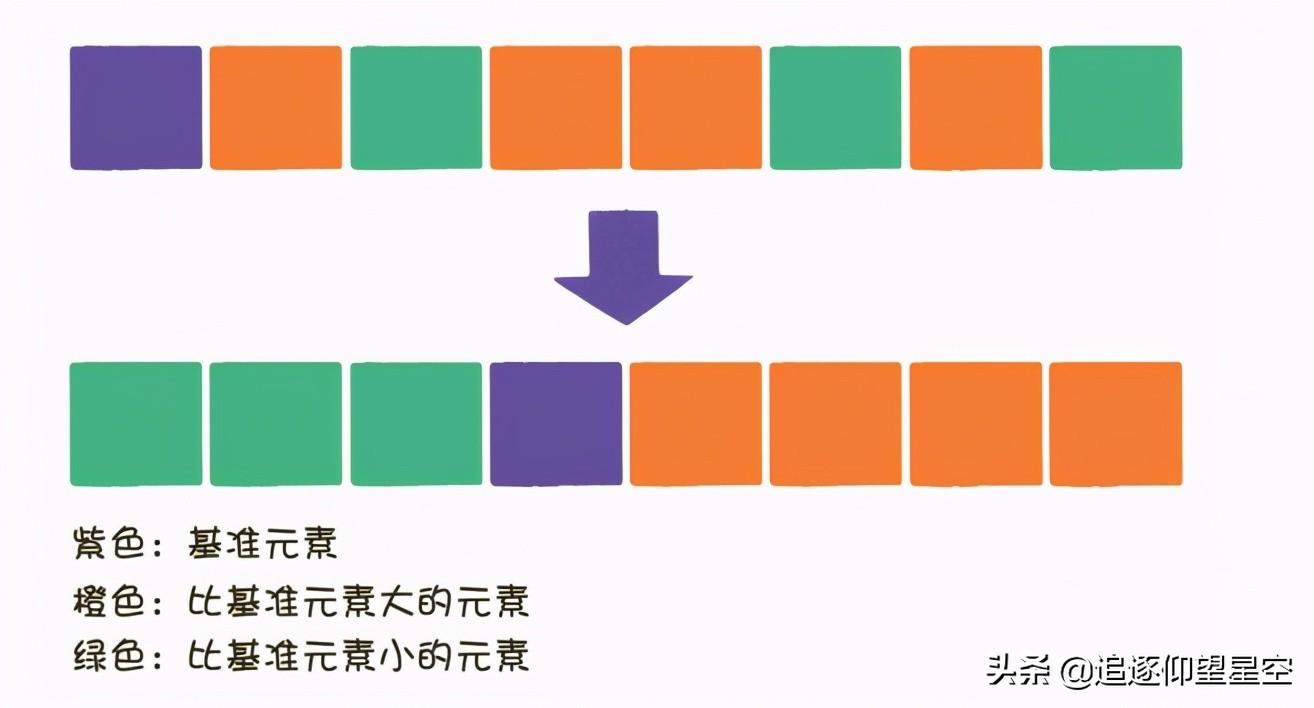
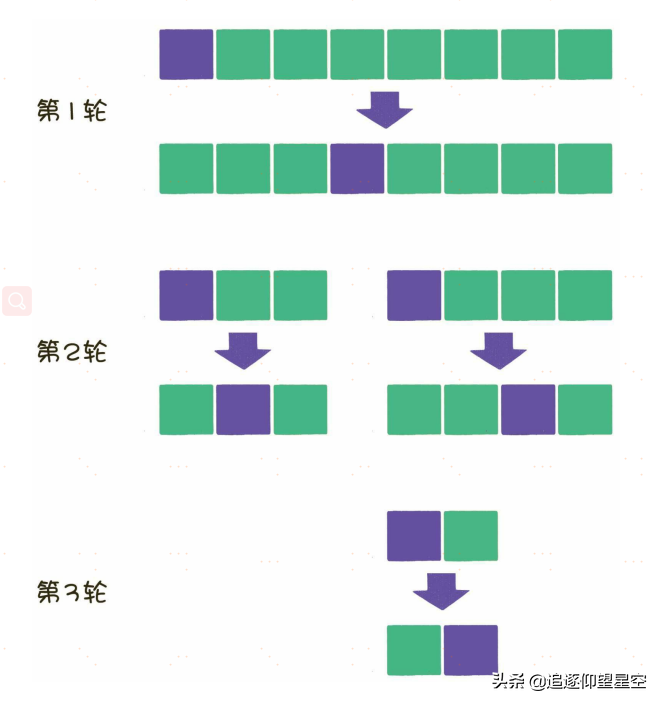
在分治法的思想下,原数列在每一轮都被拆分成两部分,每一部分在下一轮又分别被拆分成两部分,直到不可再分为止。
每一轮的比较和交换,需要把数组全部元素都遍历一遍,时间复杂度是O(n)。这样的遍历一共需要多少轮呢?假如元素个数是n,那么平均情况下需要logn轮,因此快速排序算法总体的平均时间复杂度是O(nlogn)。
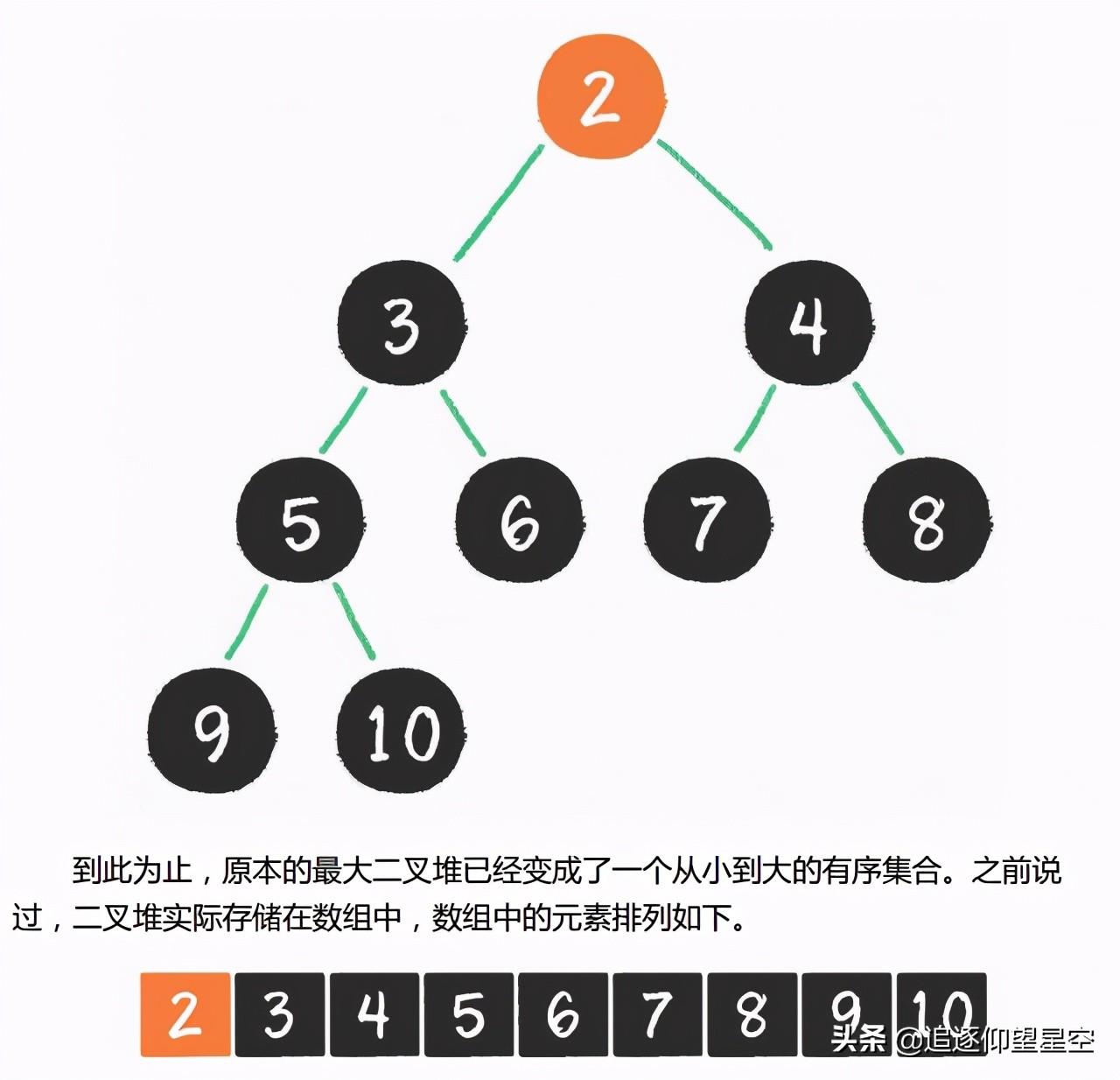
4.3 堆排序
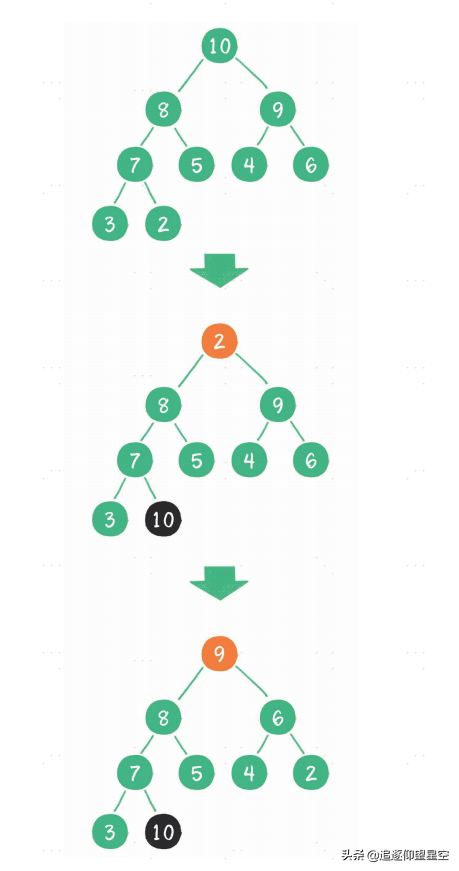
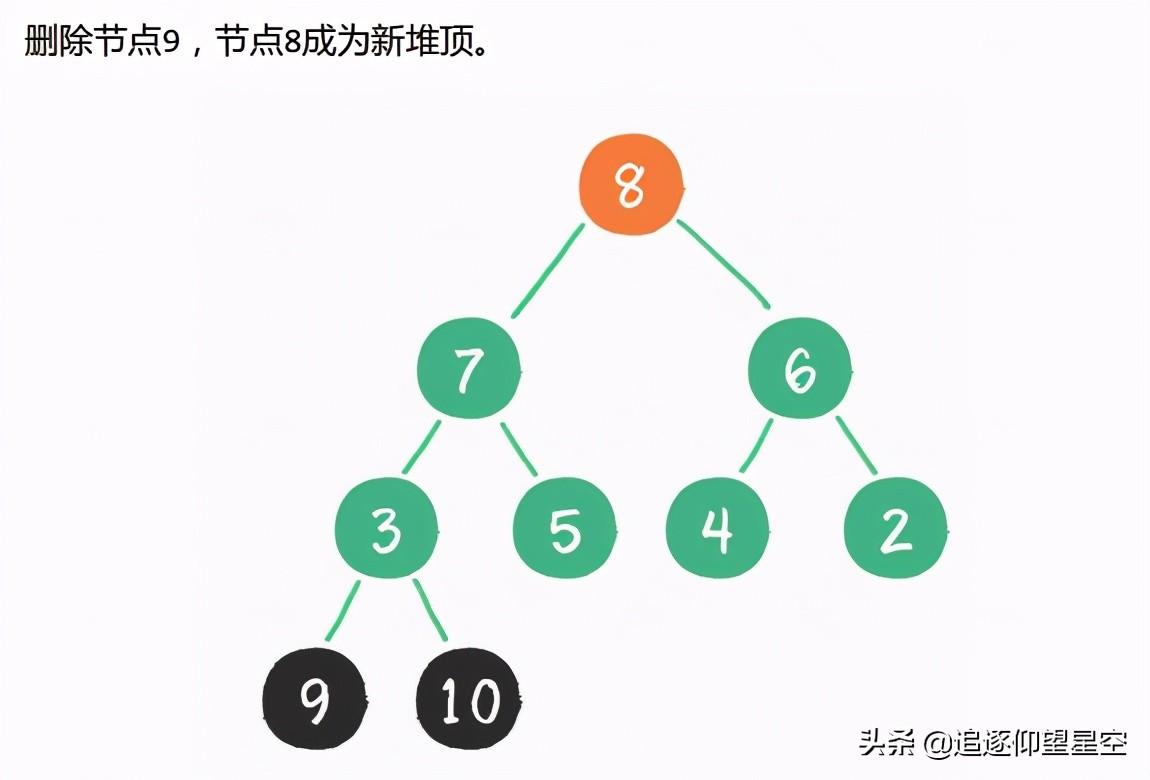
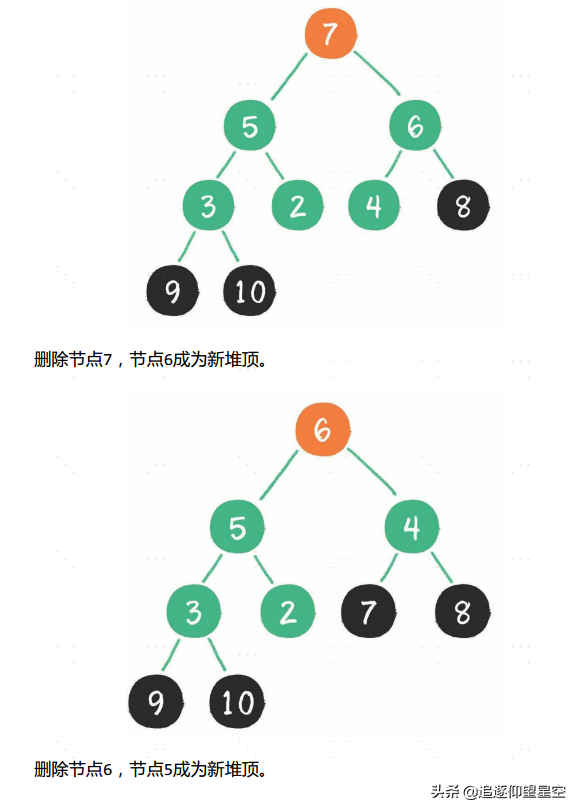
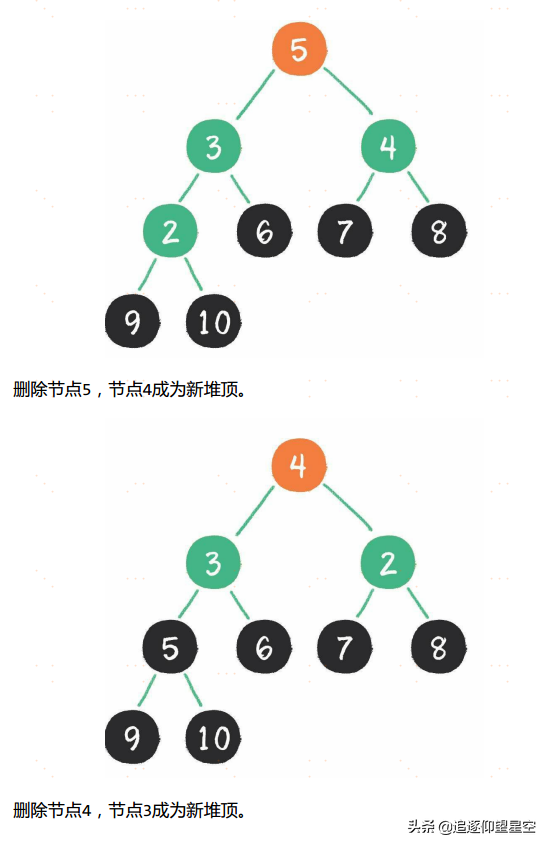
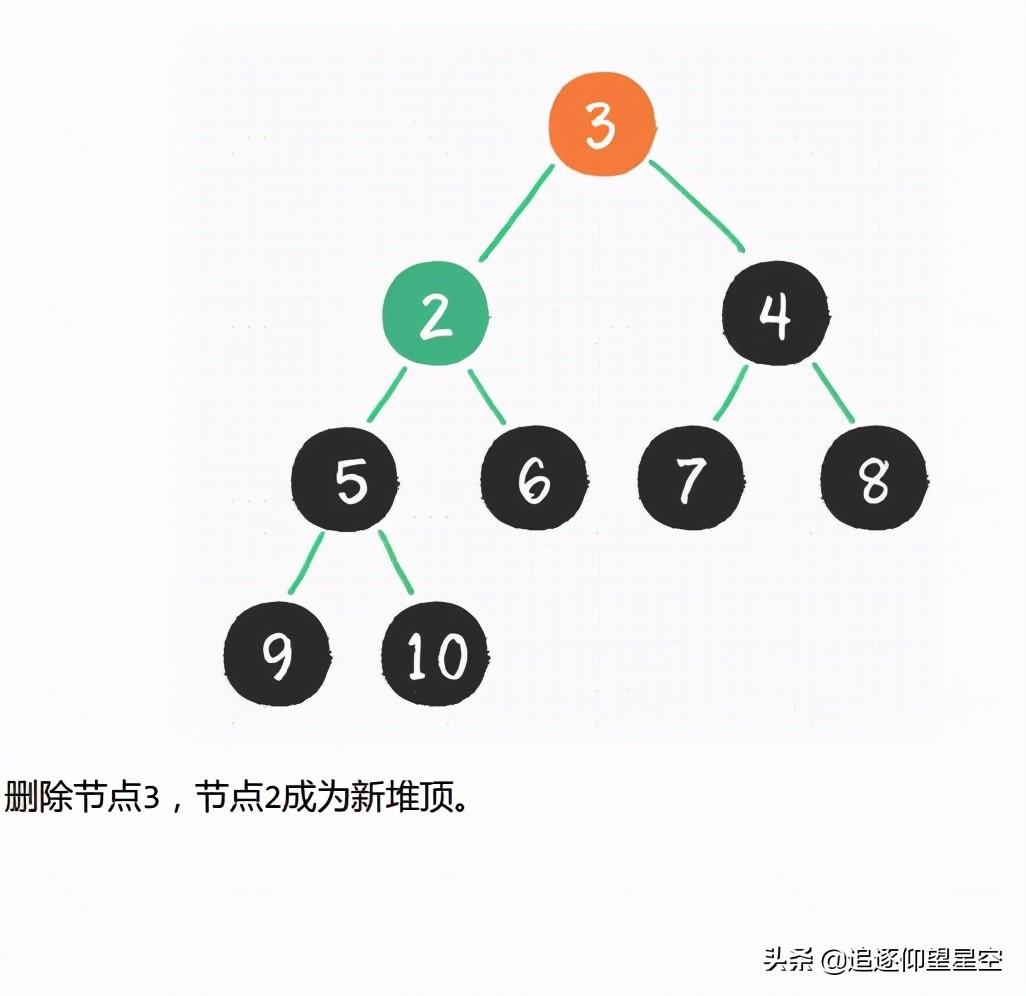
堆排序算法的步骤。
- 把无序数组构建成二叉堆。
- 循环删除堆顶元素,并将该元素移到集合尾部,调整堆产生新的堆顶。
第1步,把无序数组构建成二叉堆,这一步的时间复杂度是O(n)。
第2步,需要进行n-1次循环。每次循环调用一次downAdjust方法,所以第2步的计算规模是 (n-1)×logn ,时间复杂度为O(nlogn)。两个步骤是并列关系,所以整体的时间复杂度是O(nlogn)。
4.4 计数排序和桶排序


让我们来看看桶排序的工作原理。
桶排序的第1步,就是创建这些桶,并确定每一个桶的区间范围。

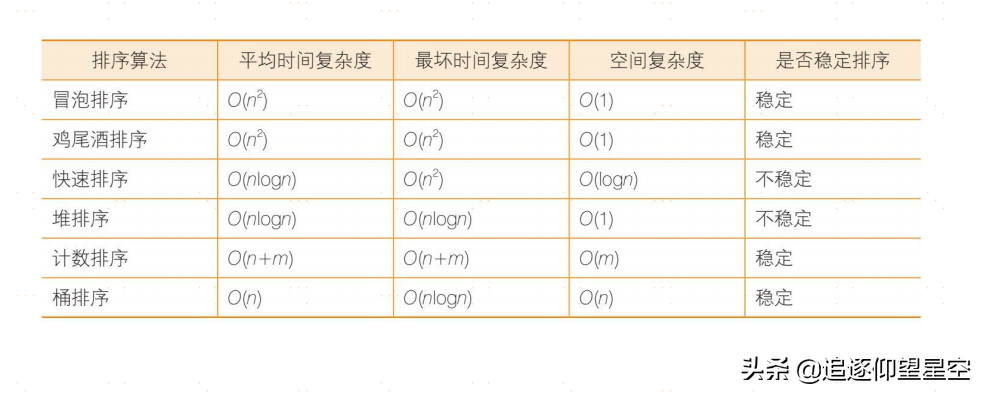
4.5 小结
 鲁公网安备37020202000738号
鲁公网安备37020202000738号