堆排序：数据结构与算法的精髓

堆排序

堆排序是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆的性质：即子节点的键值或索引总是小于（或者大于）它的父节点，堆排序的时间复杂度为O(nlogn)。(来自维基百科)

什么是堆

堆是一种特殊的完全二叉树，它的性质为：任意节点大于等于或者小于等于它的左右节点。如果任意节点大于等于它的左右节点，此堆称为最大堆；反之，任意节点小于等于它的左右节点，此堆称为最小堆。

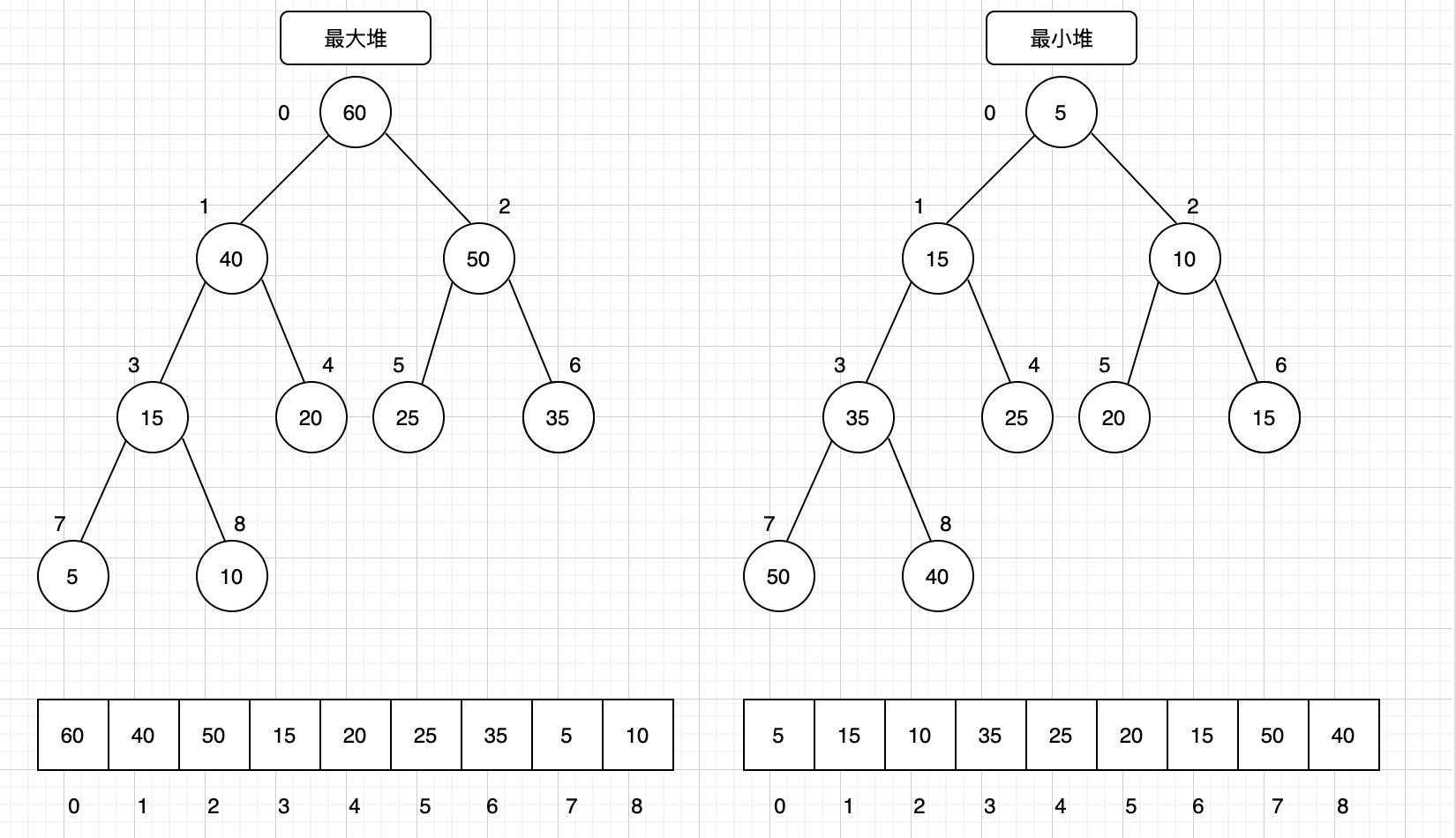
堆节点的访问

• 父节点i的左子节点所在位置(2i+1)
• 父节点i的右子节点所在位置(2i+2)
• 子节点i的父节点所在位置(i-1)/2向下取整

堆排序的基本思路

1. 无序的堆序列
2. 将每个父节点跟左右子节点作比较，将大/小的子节点和父节点做交换，直到将堆变成最小堆或者最大堆
3. 将堆顶的值跟未排序的二叉树最后的一个节点做交换
4. 重复步骤(2，3)，直到堆顶

堆排序的步骤分解

无序的序列：{0,9,6,2,3,1,5}，进行从大到小排序

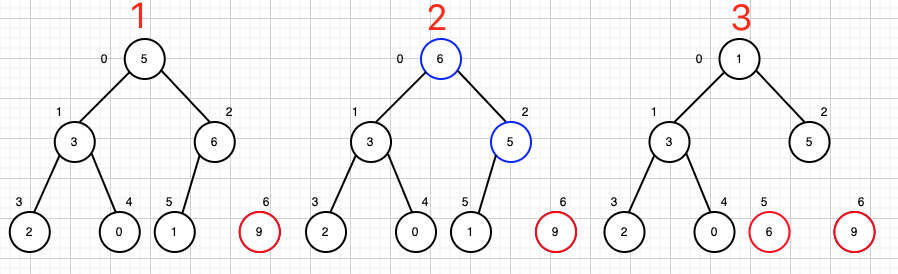
上图是构建一个初始化的最大堆，然后对堆顶和堆尾的数值作交换。

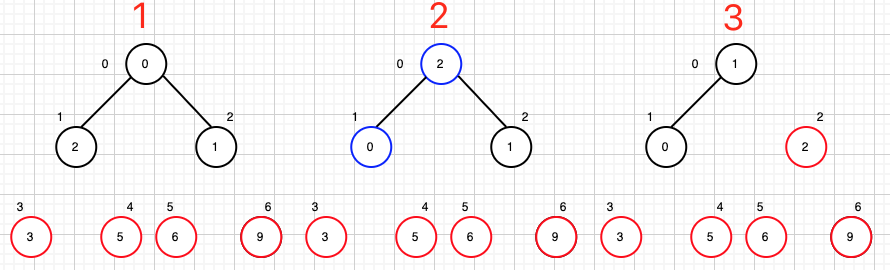
我们先对比(1)堆，从最后一个父节点开始，节点2的值都比子节点5，6都大，不需要做调整；节点1的值都比子节点3，4都大，也不需要作交换；节点0的值比左右子节点都小，然后取最大的一个子节点，(2)堆表示作交换，子节点做了交换，需要判断它的子节点是否比自己大，节点4比节点1的大(因节点4比节点3要大，故取节点4做交换)，(3)堆表示做交换。(4)堆完成了初始化的最大堆。(5)堆进行堆顶和堆尾的交换。

接下来的操作就是重复上述的流程，直到堆顶为止，看下图的流程：

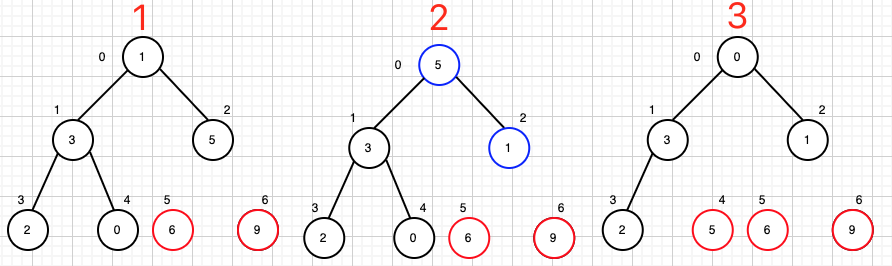
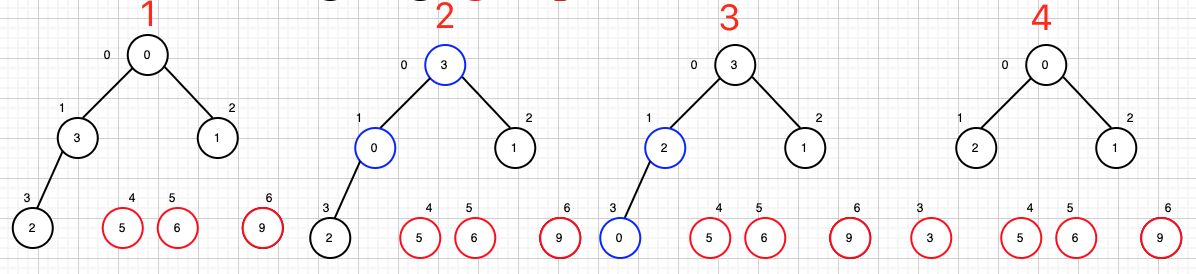
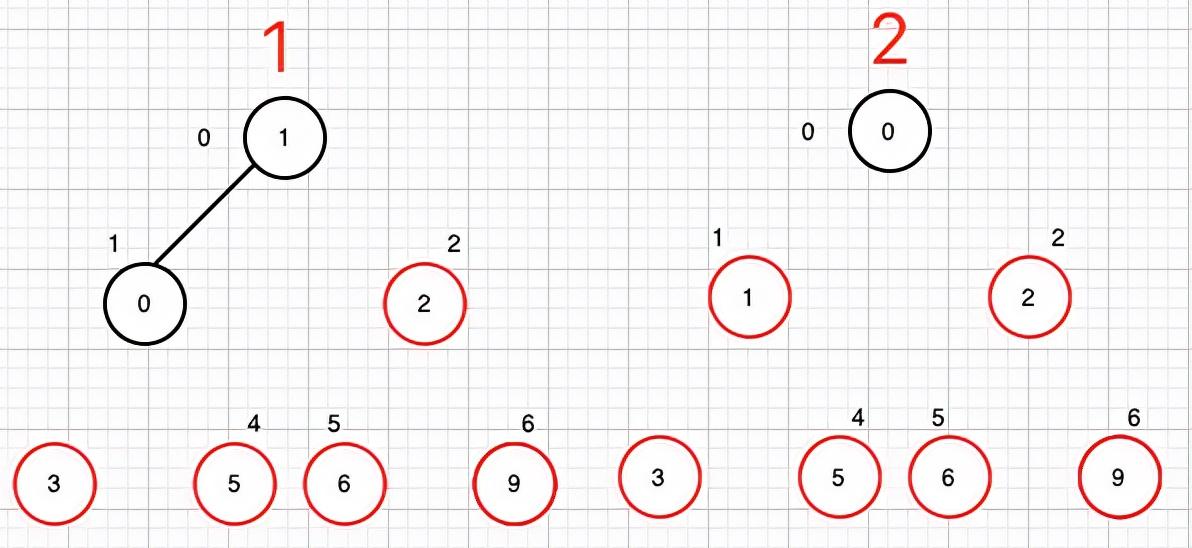
以上就是完整算法的流程。

堆排序的实现代码

void myswap(int &a, int &b) {    int tmp = a;    a = b;    b = tmp;}void MaxHead(int *pArrayNum, int nStart, int nEnd) {    int nF = nStart;//当前父节点序号    int nS = nF * 2 + 1;//当前父节点的左子节点序号    while(nS <= nEnd) {        //判断左右子节点最大值        if((nS+1 <= nEnd) && (pArrayNum[nS+1] > pArrayNum[nS])) {            nS++;//右节点大        }        //判断父节点与子节点的大小        if(pArrayNum[nS] > pArrayNum[nF]) {            //子节点比父节点大，作交换            myswap(pArrayNum[nS], pArrayNum[nF]);            //往下作对比            nF = nS;            nS = nF * 2 + 1;        }        else {            //父节点比子节点大，直接结束            return ;        }    }}void HeapSort(int *pArrayNum, int nCount) {    //初始化，构建最大堆    for(int i=nCount/2-1; i>=0; i--) {        MaxHead(pArrayNum, i, nCount-1);    }    //将堆顶的值与未排序的堆尾值做互换，然后再做堆构建    for (int i=nCount-1; i>0; i--) {        //堆顶值与未排序的堆尾值互换        myswap(pArrayNum[0], pArrayNum[i]);        MaxHead(pArrayNum, 0, i-1);//重新构建最大堆    }}

公众号有系列文章