二叉树：数据结构与算法的精髓

发表时间: 2023-01-05 18:19

笔记来源于左神的数据结构课程，代码是我在刷牛客网时做的记录

二叉树

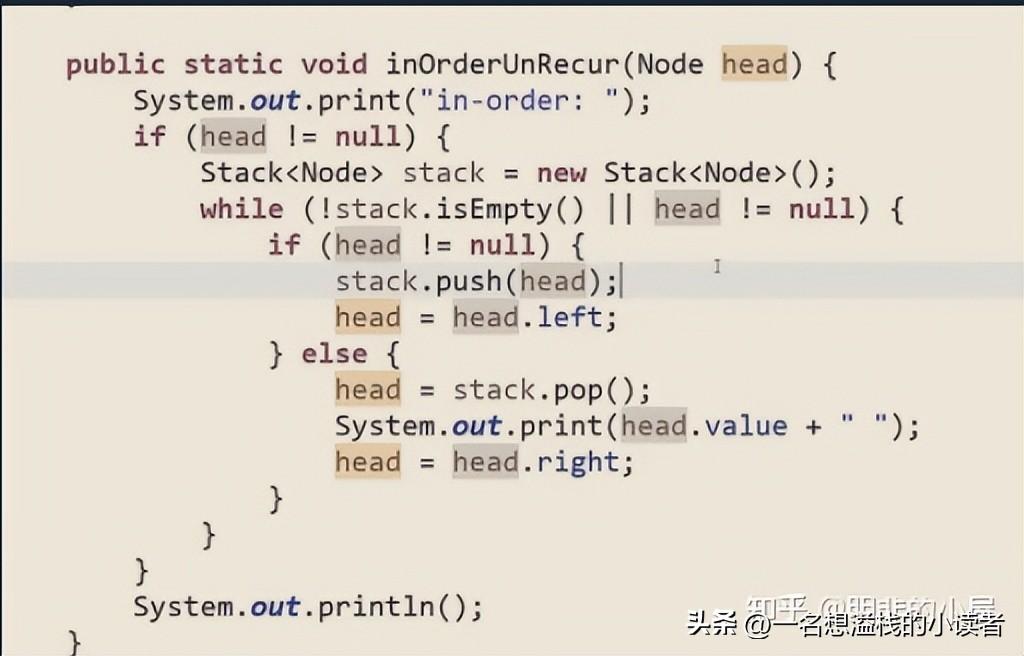
中序遍历

先把树中的左边界都放进栈，然后弹出，每弹出一个，判断是否有右边界，有的话压进栈，然后直到空弹出，周而复始

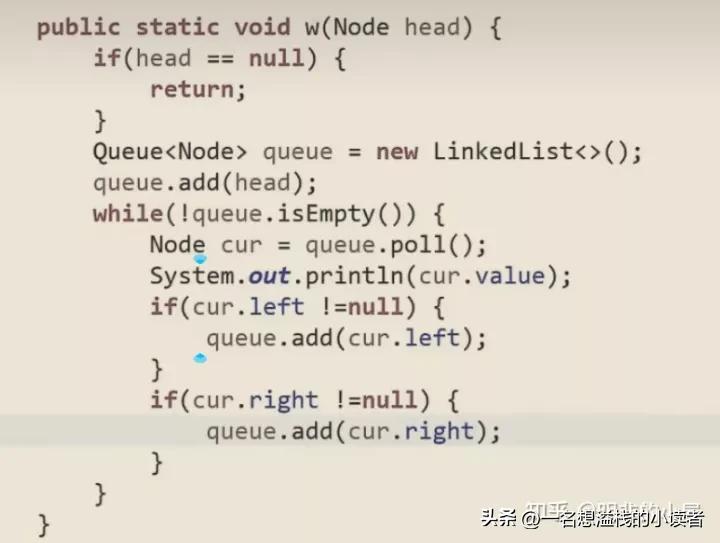
宽度优先遍历（层序遍历）

准备一个队列，头结点进，出了先放左再放右，弹出就打印

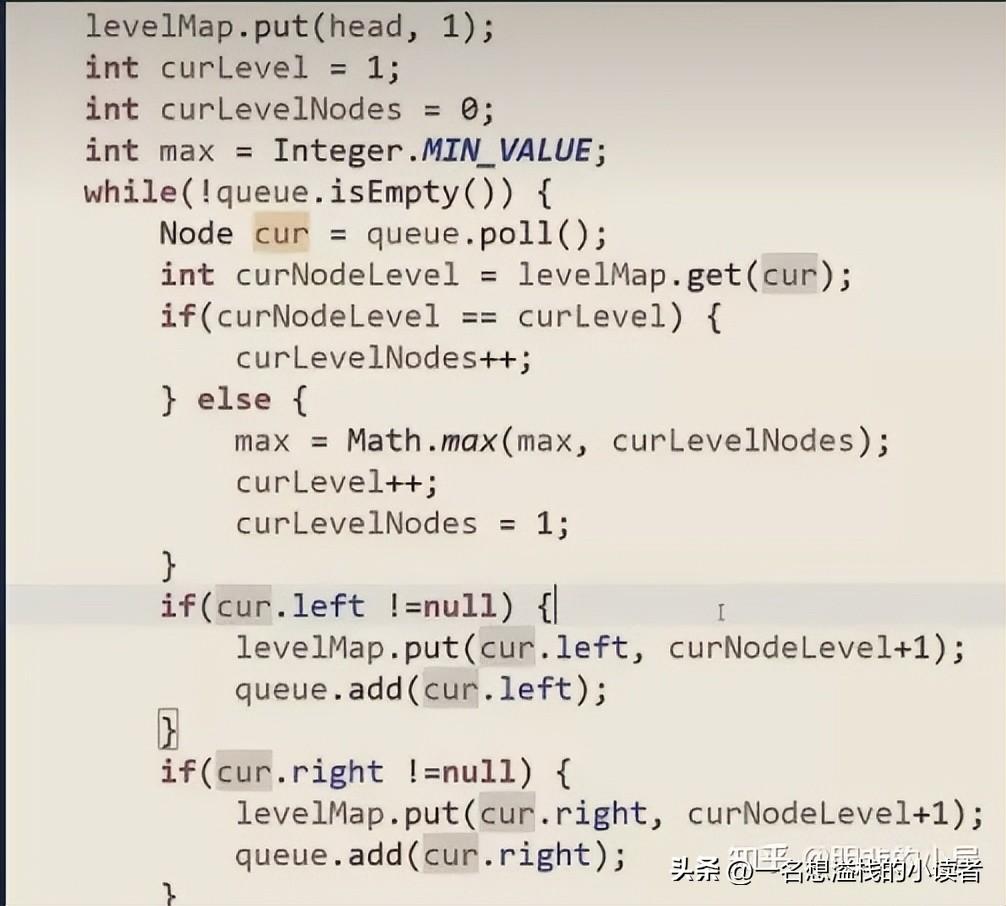
比较结束后，再循环外加一次比较，最后一层与max作比较

搜索二叉树

左树比父节点小，右树比父节点大

完全二叉树

每一层是满的，不满的层也是从左到右变满

对于任意节点，有右子无左子直接false
满足1的情况下，遇到第一个左右子不全，后续都只能是叶节点

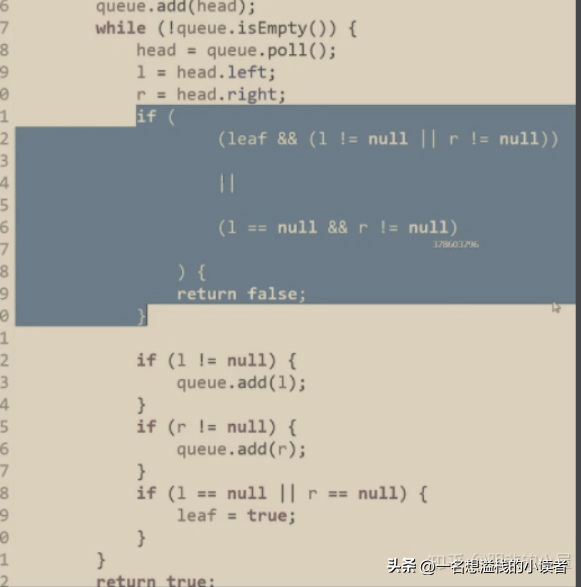
满二叉树

最大深度为：l；节点数为：n，满足n = 2**l-1

平衡二叉树

左树是平衡二叉树

右树是平衡二叉树

左树和右树的差的绝对值不大于2

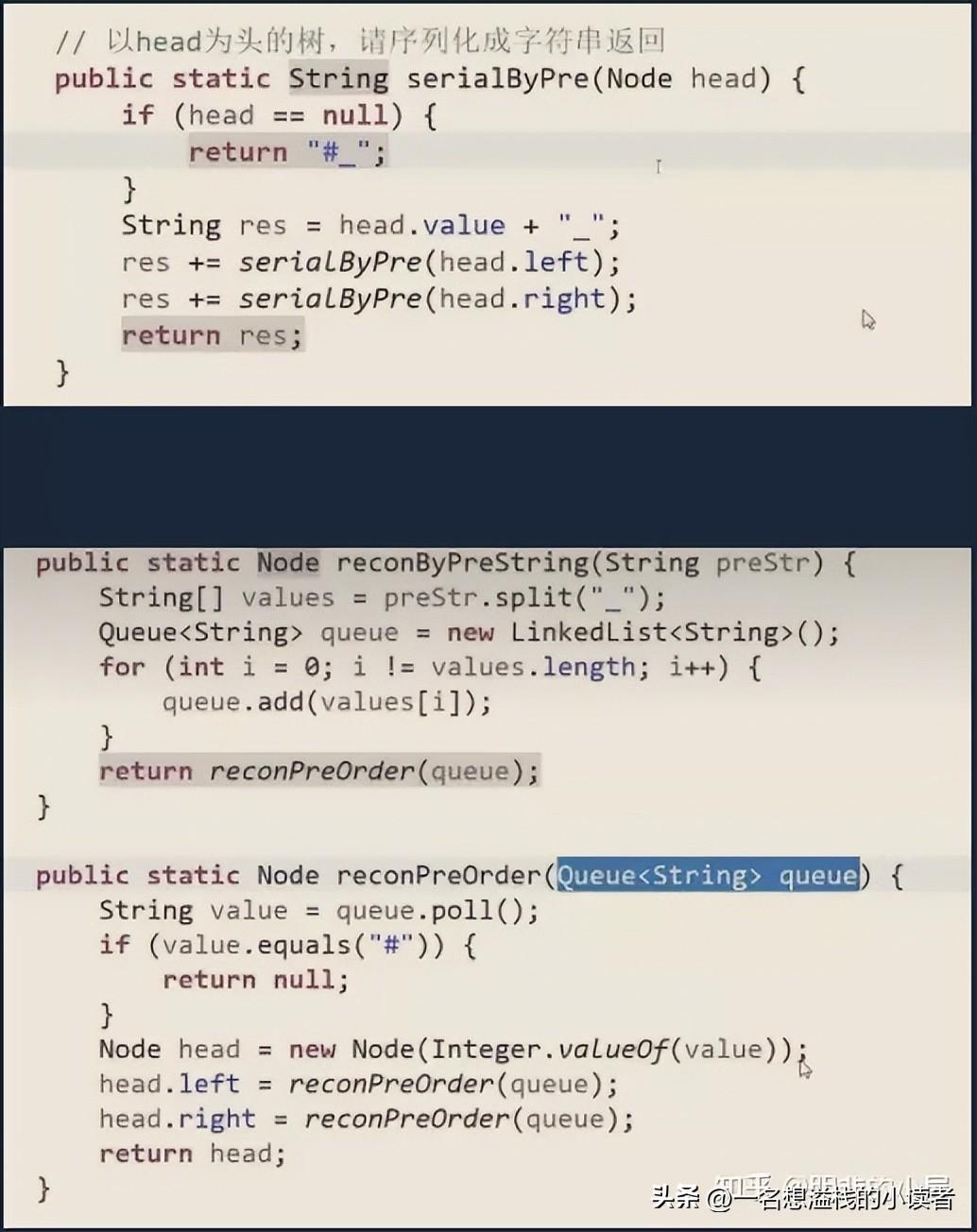
序列化和反序列化

序列化：将树转换为字符串的形式

反序列化：将字符串转换为树的形式

最低公共祖先（LCA）

先回溯所有的节点，记录所有结点的父节点，然后放进哈希表，逐个遍历

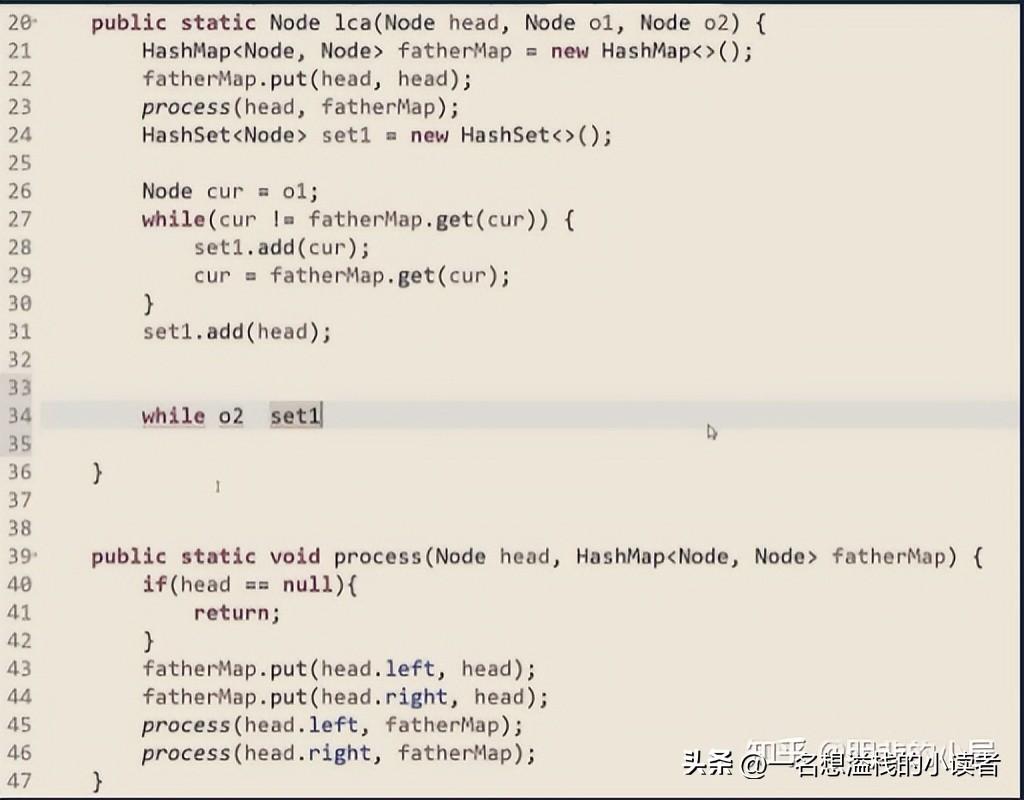
让o2往上遍历，遇到第一个set1里有的，就是最低公共祖先

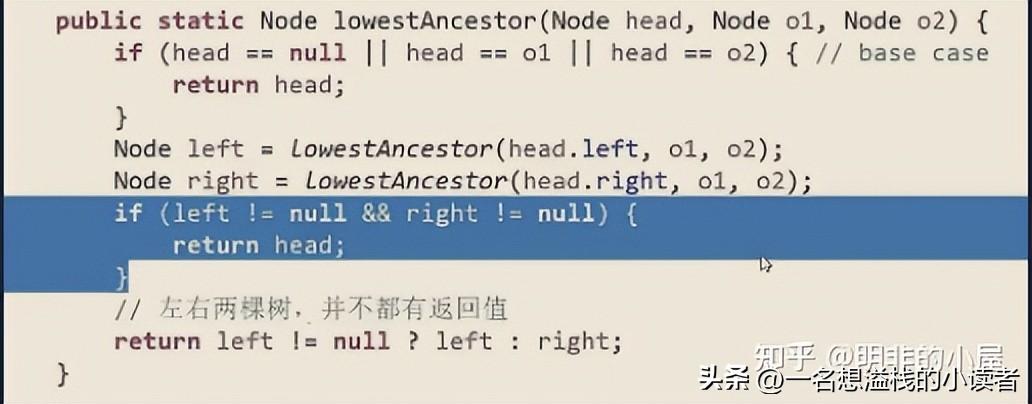
有可能情况：

o1是o2的LCA，o2是o1的LCA
o1与o2不互为LCA，回溯才能找到

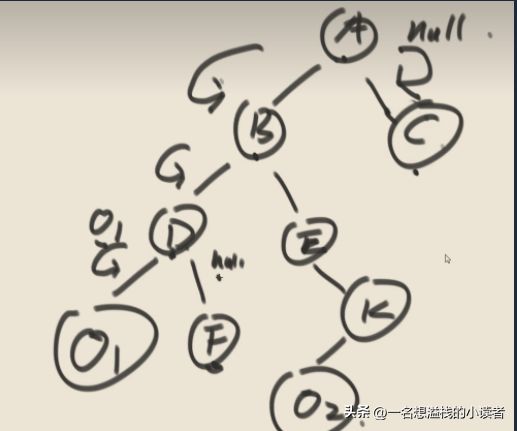
后继节点

中序遍历中节点的下一个节点

常规作法：中序遍历后生成一个序列，然后才知道后继节点，复杂度高

如果任何节点都有指向父节点的指针，复杂度变为需求的K，而不是N

如果有右树，后继节点为右树中最左节点
没有右树，上一个节点为左树的最右节点，我是我父亲的左孩子，则我的后继节点就是我父亲
还需要考虑没有后继节点的最右端孩子的情况

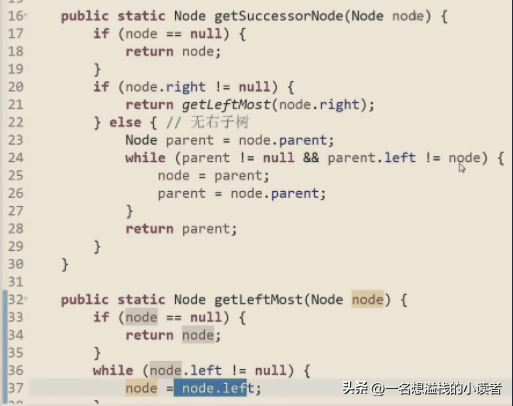
当无右子树情况，while循环条件，父是空的情况为一直往上走，但是没有父节点，即没有后继节点，返回null，则该结点是最右端结点，否则当一直为右子树结点是，结点会往父节点移，父指针也会往上指，就是在不断的往上，直到成为父的左子树

刷题

二叉树的前序遍历

递归遍历

class Solution {public:    void preorder(vector<int> &res, TreeNode *root){        if(root == NULL) return;        res.push_back(root->val);        preorder(res, root->left);        preorder(res, root->right);    }    vector<int> preorderTraversal(TreeNode* root) {        // write code here        vector<int> res;        preorder(res, root);        return res;    }};

辅助栈，每一层都先进右节点，再进左节点，然后弹出，每弹出一个都继续压入，直到空为止

class Solution {public:    vector<int> preorderTraversal(TreeNode* root) {        vector<int> res;         if(root == NULL)            return res;        //辅助栈        stack<TreeNode*> s;         //根节点先进栈        s.push(root);         //直到栈中没有节点        while(!s.empty()){             //每次栈顶就是访问的元素            TreeNode* node = s.top();             s.pop();            res.push_back(node->val);            //如果右边还有右子节点进栈            if(node->right)                 s.push(node->right);            //如果左边还有左子节点进栈            if(node->left)                 s.push(node->left);        }        return res;    }};

两种的时间复杂度和空间复杂度都为O(N)

二叉树的中序遍历

递归，不过中序遍历顺序是左头右，也是一样的思路

class Solution {public:    void inorder(vector<int> &res, TreeNode *root){        if(root == NULL) return;        inorder(res, root->left);        res.push_back(root->val);        inorder(res, root->right);    }    vector<int> inorderTraversal(TreeNode* root) {        vector<int > res;        inorder(res, root);        return res;    }};

辅助栈：头结点先入栈，然后左节点入栈，直到左节点为空，每次弹出都压入节点的右节点，如果有压入就弹出，直到回到父节点，往右树压入左节点

class Solution {public:      vector<int> inorderTraversal(TreeNode* root) {        // write code here       vector<int> res;       stack<TreeNode *> s;       while(root != NULL || !s.empty()){           while(root != NULL){               s.push(root);               root = root->left;           }           TreeNode *node = s.top();           s.pop();           res.push_back(node->val);           root = node->right;       }       return res;    }};

二叉树的后序遍历

递归，也是一样思路，左右头的顺序

class Solution {public:    void postorder(vector<int> &res, TreeNode *root){        if(root == NULL) return;        postorder(res, root->left);        postorder(res, root->right);        res.push_back(root->val);    }    vector<int> postorderTraversal(TreeNode* root) {        // write code here        vector<int> res;        postorder(res, root);        return res;    }};

辅助栈：先压左子树，然后判断右子树中值有没有遍历过，没有则压入栈，有则遍历中间节点，然后标记遍历了

class Solution {public:    vector<int> postorderTraversal(TreeNode* root) {        vector<int> res;        //辅助栈        stack<TreeNode*> s;         TreeNode* pre = NULL;         while(root != NULL || !s.empty()){             //每次先找到最左边的节点            while(root != NULL){                 s.push(root);                root = root->left;            }            //弹出栈顶            TreeNode* node = s.top();             s.pop();            //如果该元素的右边没有或是已经访问过            if(node->right == NULL || node->right == pre){                 //访问中间的节点                res.push_back(node->val);                 //且记录为访问过了                pre = node;             }else{                //该节点入栈                s.push(node);                //先访问右边                root = node->right;             }        }        return res;    }};

二叉树的层序遍历

队列方式：对于每一层的节点，可以遍历下一层的所有节点，从左到右分别入队列，然后依次弹出，在栈中储存入队列时的值，出队一个即可知道该值

class Solution {public:    vector<vector<int> > levelOrder(TreeNode* root) {        vector<vector<int> > res;        if(root == NULL)            //如果是空，则直接返回空vector            return res;         //队列存储，进行层次遍历        queue<TreeNode*> q;         q.push(root);        TreeNode* cur;        while(!q.empty()){            //记录二叉树的某一行            vector<int> row;              int n = q.size();            //因先进入的是根节点，故每层节点多少，队列大小就是多少            for(int i = 0; i < n; i++){                cur = q.front();                q.pop();                row.push_back(cur->val);                //若是左右孩子存在，则存入左右孩子作为下一个层次                if(cur->left)                    q.push(cur->left);                if(cur->right)                    q.push(cur->right);            }            //每一层加入输出            res.push_back(row);         }        return res;    }};

递归方式：每一层都记录当前二叉树的深度，遍历的时候从左到右，递归也是从左到右

class Solution {public:    void traverse(TreeNode* root, vector<vector<int>>& res, int depth) {        if(root){            //新的一层            if(res.size() < depth)                  res.push_back(vector<int>{});             //vector从0开始计数因此减1，在节点当前层的vector中插入节点            res[depth - 1].push_back(root->val);        }        else            return;        //递归左右时进入下一层        traverse(root->left, res, depth + 1);         traverse(root->right, res, depth + 1);    }        vector<vector<int> > levelOrder(TreeNode* root) {        vector<vector<int> > res;        if(root == NULL)            //如果是空，则直接返回空vector            return res;         traverse(root, res, 1);        return res;    }};

按之字型顺序打印二叉树

队列方式，判断当前处于第几层，偶数从左到右打印，奇数从右到左，采用入队列方式

class Solution {public:    vector<vector<int> > Print(TreeNode* pRoot) {        vector<vector<int> > res;         if (!pRoot)            return res;         queue<TreeNode*> q; // 定义队列        q.push(pRoot); // 根结点入队列        int level = 0;        while (!q.empty()) {            vector<int> arr; // 定义数组存储每一行结果            int size = q.size(); // 当前队列长度            for (int i = 0; i < size; i++) {                TreeNode* tmp = q.front(); // 队头元素                q.pop();                 if (!tmp) // 空元素跳过                    continue;                q.push(tmp->left); // 左孩子入队列                q.push(tmp->right); // 右孩子入队列                if (level % 2 == 0) {                    // 从左至右打印                    arr.push_back(tmp->val);                } else { // 从右至左打印                    arr.insert(arr.begin(), tmp->val);                }            }            level++; // 下一层，改变打印方向            if (!arr.empty())                res.push_back(arr); // 放入最终结果        }        return res;    }};

两个栈的方式，第一个栈从右到左放，第二个栈从左到右放，弹出的时候顺序相反，每一层只用一种栈，用完一种用另一种，直到两个栈为空

class Solution {public:    vector<vector<int> > Print(TreeNode* pRoot) {        vector<vector<int> > res;         if (!pRoot)             return res;         stack<TreeNode*> stk1, stk2; // 定义两个栈        stk1.push(pRoot); // 根结点入栈        while (!stk1.empty() || !stk2.empty()) { // 两个栈全空时循环结束            vector <int> arr;             while (!stk1.empty()) {                TreeNode* p = stk1.top();                 stk1.pop();                 arr.push_back(p->val); // 访问栈顶                if (p->left) stk2.push(p->left); // 左孩子入栈                if (p->right) stk2.push(p->right); // 右孩子入栈            }            if (arr.size())                res.push_back(arr); // 保存结果            arr.clear(); // 清空            while (!stk2.empty()) {                TreeNode* p = stk2.top();                 stk2.pop();                 arr.push_back(p->val); // 访问栈顶                if (p->right) stk1.push(p->right); // 右孩子入栈                if (p->left) stk1.push(p->left); // 左孩子入栈            }            if (arr.size())                res.push_back(arr); // 保存结果        }        return res;    }};

二叉树的最大深度

递归方式：分别遍历到左边最大深度和右边最大深度，再加上头结点的1，取最大的那个即可

class Solution {public:    int maxDepth(TreeNode* root) {        //空节点没有深度        if(root == NULL)             return 0;        //返回子树深度+1        return max(maxDepth(root->left), maxDepth(root->right)) + 1;     }};

队列方式：如果还有节点，就不断执行入队操作，然后记录层数

class Solution {public:    int maxDepth(TreeNode* root) {        if(root == NULL) return 0 ;        queue<TreeNode*> q;        q.push(root);        int res = 0;        while(!q.empty()){            int n = q.size();            for(int i= 0; i< n; i++){                TreeNode *node = q.front();                q.pop();                if(node->left) q.push(node->left);                if(node->right) q.push(node->right);            }            res++;        }        return res;    }};

二叉树中和为某一值的路径

递归方式：对于每一层，用sum减去当前数值，如果为0，而且左子树和右子树都不存在，那么就是true，否则为false。然后递归到下一层，下一层的sum为上一层的sum减去的值。

class Solution {public:    bool hasPathSum(TreeNode* root, int sum) {        // write code here        if(root == NULL) return false;        if(root->left == NULL && root->right == NULL && sum - root->val == 0) return true;        return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);    }};

辅助栈：使用两个栈，一个记录节点，一个记录当前路径和，即sum，进行深度优先遍历

class Solution {public:    bool hasPathSum(TreeNode* root, int sum) {        // write code here        if(root == NULL) return false;        stack<pair<TreeNode *, int>> s;        s.push({root, root->val});        while(!s.empty()){            auto temp = s.top();            s.pop();            if(temp.first->left == NULL && temp.first->right == NULL && temp.second == sum) return true;            if(temp.first->left != NULL){                s.push({temp.first->left, temp.second + temp.first->left->val});            }            if(temp.first->right != NULL){                s.push({temp.first->right, temp.second + temp.first->right->val});            }        }        return false;    }};

二叉搜索树与双向链表

采用递归方式，把遍历的节点按中序遍历放入数组中，然后依次给数组中元素加上方向，变成哈希表

class Solution {public:    vector<TreeNode*> TreeList;	void inorder(TreeNode* root){		if(!root) return;		inorder(root->left);		TreeList.push_back(root);		inorder(root->right);	}	TreeNode* Convert(TreeNode* pRootOfTree) {        if(!pRootOfTree) return pRootOfTree;		inorder(pRootOfTree);		for(int i=0; i<TreeList.size() - 1; i++){			TreeList[i]->right = TreeList[i+1];			TreeList[i+1]->left = TreeList[i];		}		return TreeList[0];    }};

中序遍历方式找到最左节点，然后依次定义双向指针

class Solution {public:    //返回的第一个指针，即为最小值，先定为NULL    TreeNode* head = NULL;      //中序遍历当前值的上一位，初值为最小值，先定为NULL    TreeNode* pre = NULL;       TreeNode* Convert(TreeNode* pRootOfTree) {        if(pRootOfTree == NULL)            //中序递归，叶子为空则返回            return NULL;             //首先递归到最左最小值           Convert(pRootOfTree->left);         //找到最小值，初始化head与pre        if(pre == NULL){                   head = pRootOfTree;            pre = pRootOfTree;        }        //当前节点与上一节点建立连接，将pre设置为当前值        else{                   pre->right = pRootOfTree;            pRootOfTree->left = pre;            pre = pRootOfTree;        }        Convert(pRootOfTree->right);        return head;    }};

对称二叉树

双指针分别进行相反方向的遍历，只要不满足数量和位置都为false

class Solution {public:    bool recursion(TreeNode* root1, TreeNode* root2){        //可以两个都为空        if(root1 == NULL && root2 == NULL)             return true;        //只有一个为空或者节点值不同，必定不对称        if(root1 == NULL || root2 == NULL || root1->val != root2->val)            return false;        //每层对应的节点进入递归        return recursion(root1->left, root2->right) && recursion(root1->right, root2->left);    }    bool isSymmetrical(TreeNode* pRoot) {        return recursion(pRoot, pRoot);    }};

队列的方式，采用两个队列，按照对称的顺序入队，然后弹出判断，继续入队，判断直到空

class Solution {public:    bool isSymmetrical(TreeNode* pRoot) {        //空树为对称的        if(pRoot == NULL)             return true;        //辅助队列用于从两边层次遍历        queue<TreeNode*> q1;         queue<TreeNode*> q2;        q1.push(pRoot->left);        q2.push(pRoot->right);        while(!q1.empty() && !q2.empty()){             //分别从左边和右边弹出节点            TreeNode* left = q1.front();             q1.pop();            TreeNode* right = q2.front();            q2.pop();            //都为空暂时对称            if(left == NULL && right == NULL)                continue;            //某一个为空或者数字不相等则不对称            if(left == NULL || right == NULL || left->val != right->val)                return false;            //从左往右加入队列            q1.push(left->left);             q1.push(left->right);            //从右往左加入队列            q2.push(right->right);             q2.push(right->left);        }        //都检验完都是对称的        return true;     }};

合并二叉树

递归方式：如果有一个树没有节点，就返回另一个树的，如果有就相加，然后分别递归两子树的左树和右树

class Solution {public:    TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {        // write code here      	if(t1 == NULL) return t2;      	if(t2 == NULL) return t1;        TreeNode *head = new TreeNode(t1->val+t2->val);        head->left = mergeTrees(t1->left, t2->left);        head->right = mergeTrees(t1->right, t2->right);        return head;    }};

队列方式：申请三个队列，分别入队后弹出，思路比较简单，但是代码较长，繁琐了些

class Solution {public:    TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {        //若只有一个节点返回另一个，两个都为NULL自然返回NULL        if (t1 == NULL)            return t2;        if (t2 == NULL)            return t1;        //合并根节点        TreeNode* head = new TreeNode(t1->val + t2->val);         //连接后的树的层次遍历节点        queue<TreeNode*> q;         //分别存两棵树的层次遍历节点        queue<TreeNode*> q1;         queue<TreeNode*> q2;        q.push(head);        q1.push(t1);          q2.push(t2);        while (!q1.empty() && !q2.empty()) {            TreeNode *node = q.front(), *node1 = q1.front(), *node2 = q2.front();            q.pop();            q1.pop();            q2.pop();            TreeNode *left1 = node1->left, *left2 = node2->left, *right1 = node1->right, *right2 = node2->right;            //两个左节点都存在            if (left1 || left2) {                 if (left1 && left2) {                    TreeNode* left = new TreeNode(left1->val + left2->val);                    node->left = left;                     //新节点入队列                    q.push(left);                     q1.push(left1);                    q2.push(left2);                //只连接一个节点                } else if (left1)                     node->left = left1;                  else if (left2)                     node->left = left2;            }            if (right1 || right2) {                //两个右节点都存在                if (right1 && right2) {                     TreeNode* right = new TreeNode(right1->val + right2->val);                    node->right = right;                    //新节点入队列                    q.push(right);                     q1.push(right1);                    q2.push(right2);                //只连接一个节点                } else if (right1)                      node->right = right1;                  else                     node->right = right2;            }        }        return head;    }};

二叉树的镜像

递归方式：镜像即交换左节点和右节点，直接把左右的节点递归交换即可

class Solution {public:    TreeNode* Mirror(TreeNode* pRoot) {        // write code here        if(pRoot == NULL) return pRoot;        swap(pRoot->left, pRoot->right);        Mirror(pRoot->left);        Mirror(pRoot->right);        return pRoot;    }};

栈的方式：前序遍历，入一个结点即弹出该结点，然后左子树右子树入栈，弹出后交换

class Solution {public:    TreeNode* Mirror(TreeNode* pRoot) {        // write code here        if(pRoot == NULL) return pRoot;        stack<TreeNode *> s;        s.push(pRoot);        while(!s.empty()){            TreeNode *node = s.top();            s.pop();            if(node->left != NULL) s.push(node->left);            if(node->right != NULL) s.push(node->right);            TreeNode *temp = node->right;            node->right = node->left;            node->left = temp;        }        return pRoot;    }};

判断二叉搜索树

递归的方式：

首先递归到最左，初始化maxLeft与pre。
然后往后遍历整棵树，依次连接pre与当前节点，并更新pre。
左子树如果不是二叉搜索树返回false。
判断当前节点是不是小于前置节点，更新前置节点。
最后由右子树的后面节点决定。

class Solution {public:    long pre = INT_MIN;    bool isValidBST(TreeNode* root) {        // write code here        if(root == NULL) return true;        if(!isValidBST(root->left)) return false;        if(root->val <= pre) return false;        pre = root->val;        if(!isValidBST(root->right)) return false;        return true;    }};

栈的方式：先把每次进入的左节点遍历到最后，然后依次弹出，每次弹出都检查是否有右节点，有的话入栈继续该过程，将弹出的值放入数组中，最后遍历数组中的值，是否为升序或者降序

public:    long pre = INT_MIN;    bool isValidBST(TreeNode* root) {        // write code here        stack<TreeNode *> s;        TreeNode *head = root;        vector<int> sort;        while(head != NULL || !s.empty()){            while(head != NULL){                s.push(head);                head = head->left;            }            head = s.top();            s.pop();            sort.push_back(head->val);            head = head->right;        }        for(int i=1; i<sort.size(); i++){            if(sort[i-1] > sort[i]) return false;        }        return true;    }};

判断是不是完全二叉树

首先判断空树是完全二叉树，采用队列方式，每次入队一个层次，如果该层没有空节点则继续遍历，如果有空节点就设置flag为TRUE，即标志着有空节点，接下去不应该有下一个

 bool isCompleteTree(TreeNode* root) {        if(root == NULL) return true;        queue<TreeNode *> q;        q.push(root);        bool flag = false;        while(!q.empty()){            int sz = q.size();            for(int i=0; i<sz; i++){                TreeNode *cur = q.front();                q.pop();                if(cur == NULL) flag = true;                else{                    if(flag) return false;                    q.push(cur->left);                    q.push(cur->right);                }            }        }        return true;    }

判断是不是平衡二叉树

自底向上的思路，先求出左树和右树的高度，递归得到左树右树是否为平衡二叉树，最后判断左树和右树的绝对值是否相差1

class Solution {public:    int depth(TreeNode *root){        if(!root) return 0;        int ldep = depth(root->left);        if(ldep == -1) return -1;        int rdep = depth(root->right);        if(rdep == -1) return -1;        int sub = abs(ldep - rdep);        if(sub > 1) return -1;        return max(ldep, rdep) + 1;    }    bool IsBalanced_Solution(TreeNode* pRoot) {        return depth(pRoot) != -1;    }};

二叉搜索树的最低公共祖先

查找两节点的最近的公共祖先，在这里我是采用左神的思路，如果遇到了只遇到其中一个结点，那就直接返回该结点，另一个结点一定是它的子节点；如果两节点不在同一边的树，那最终就会返回头结点；最后一种就是返回两节点往上返回时遇到的第一个结点，因为这个结点的左右不为空，所以会是公共祖先。

这种方法可以适用于普通二叉树

   TreeNode *dfs(TreeNode *head, int o1, int o2){        if(!head || head->val == o1 || head->val == o2) return head;        TreeNode *left = dfs(head->left,o1,o2);        TreeNode *right = dfs(head->right,o1,o2);        if(left != NULL && right != NULL) return head;        return left != NULL ? left :right;    }    int lowestCommonAncestor(TreeNode* root, int p, int q) {        // write code here        return dfs(root, p, q)->val;    }

比较法，因为这是二叉搜索树，可以先判断pq与节点大小关系

class Solution {public:    int lowestCommonAncestor(TreeNode* root, int p, int q) {        //空树找不到公共祖先        if(root == NULL)            return -1;        //pq在该节点两边说明这就是最近公共祖先        if((p >= root->val && q <= root->val) || (p <= root->val && q >= root->val))            return root->val;        //pq都在该节点的左边        else if(p <= root->val && q <= root->val)            //进入左子树            return lowestCommonAncestor(root->left, p, q);        //pq都在该节点的右边        else            //进入右子树            return lowestCommonAncestor(root->right, p, q);    }};

重建二叉树

通过前序遍历确定头结点，然后找到头结点在中序遍历所在位置，分为左子树和右子树，然后递归该过程

class Solution {  public:    TreeNode* reConstructBinaryTree(vector<int> pre, vector<int> vin) {        int n = pre.size();        int m = vin.size();        if (n == 0 || m == 0) return NULL;        TreeNode* root = new TreeNode(pre[0]);        for (int i = 0; i < vin.size(); i++) {            if (pre[0] == vin[i]) {                vector<int> leftpre(pre.begin() + 1, pre.begin() + i + 1);                vector<int> leftvin(vin.begin() , vin.begin() + i );                root->left = reConstructBinaryTree(leftpre, leftvin);                vector<int> rigthpre(pre.begin() +i+ 1, pre.end());                vector<int> rightvin(vin.begin() +i+ 1, vin.end());                root->right = reConstructBinaryTree(rigthpre, rightvin);                break;            }        }        return root;    }};

二叉树的右视图

首先检查两个遍历序列的大小，若是为0，则空树不用打印。
建树函数根据上述说，每次利用前序遍历第一个元素就是根节点，在中序遍历中找到它将二叉树划分为左右子树，利用l1 r1 l2 r2分别记录子树部分在数组中分别对应的下标，并将子树的数组部分送入函数进行递归。
dfs打印右视图时，使用哈希表存储每个深度对应的最右边节点，初始化两个栈辅助遍历，第一个栈记录dfs时的节点，第二个栈记录遍历到的深度，根节点先入栈。
对于每个访问的节点，每次左子节点先进栈，右子节点再进栈，这样访问完一层后，因为栈的先进后出原理，每次都是右边被优先访问，因此我们在哈希表该层没有元素时，添加第一个该层遇到的元素就是最右边的节点。
使用一个变量逐层维护深度最大值，最后遍历每个深度，从哈希表中读出每个深度的最右边节点加入数组中。

class Solution {public:    //建树函数    //四个int参数分别是前序最左节点下标，前序最右节点下标    //中序最左节点下标，中序最右节点坐标    TreeNode* buildTree(vector<int>& xianxu, int l1, int r1, vector<int>& zhongxu, int l2, int r2) {        if(l1 > r1 || l2 > r2)            return NULL;        //构建节点        TreeNode* root = new TreeNode(xianxu[l1]);         //用来保存根节点在中序遍历列表的下标          int rootIndex = 0;            //寻找根节点        for(int i = l2; i <= r2; i++){            if(zhongxu[i] == xianxu[l1]){                rootIndex = i;                break;            }        }        //左子树大小        int leftsize = rootIndex - l2;            //右子树大小        int rightsize = r2 - rootIndex;            //递归构建左子树和右子树        root->left = buildTree(xianxu, l1 + 1, l1 + leftsize, zhongxu, l2 , l2 + leftsize - 1);        root->right = buildTree(xianxu, r1 - rightsize + 1, r1, zhongxu, rootIndex + 1, r2);        return root;    }    //深度优先搜索函数    vector<int> rightSideView(TreeNode* root) {        //右边最深处的值        unordered_map<int, int> mp;        //记录最大深度        int max_depth = -1;         //维护深度访问节点        stack<TreeNode*> nodes;         //维护dfs时的深度        stack<int> depths;          nodes.push(root);         depths.push(0);        while (!nodes.empty()){            TreeNode* node = nodes.top();            nodes.pop();            int depth = depths.top();            depths.pop();            if (node != NULL) {            	//维护二叉树的最大深度                max_depth = max(max_depth, depth);                //如果不存在对应深度的节点我们才插入                if (mp.find(depth) == mp.end())                    mp[depth] =  node->val;                nodes.push(node->left);                nodes.push(node->right);                depths.push(depth + 1);                depths.push(depth + 1);            }        }        vector<int> res;        for (int i = 0; i <= max_depth; i++)            res.push_back(mp[i]);        return res;    }    vector<int> solve(vector<int>& xianxu, vector<int>& zhongxu) {        vector<int> res;        //空节点        if(xianxu.size() == 0)             return res;        //建树        TreeNode* root = buildTree(xianxu, 0, xianxu.size() - 1, zhongxu, 0, zhongxu.size() - 1);        //找每一层最右边的节点        return rightSideView(root);    }};

使用队列和栈的方法，把当前层次的节点都放入，然后当该层的节点都遍历完，取最后一个结点就是最右的节点

class Solution {public:    /**     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可     * 求二叉树的右视图     * @param xianxu int整型vector 先序遍历     * @param zhongxu int整型vector 中序遍历     * @return int整型vector     */     unordered_map<int, int> index;    TreeNode *buildTree(vector<int>& xianxu, int l1, int r1, vector<int>& zhongxu, int l2, int r2){        if(l1>r1 || l2>r2)return NULL;        TreeNode *root = new TreeNode(xianxu[l1]);        int rootIndex = 0;        for(int i=l2; i<=r2; i++){            if(zhongxu[i] == xianxu[l1]){                rootIndex = i;                break;            }        }        int leftsize = rootIndex - l2;        int rightsize = r2 - rootIndex;        root->left = buildTree(xianxu,l1+1, l1+leftsize, zhongxu, l2, l2+leftsize-1);        root->right = buildTree(xianxu, r1 - rightsize + 1, r1, zhongxu, rootIndex + 1, r2);        return root;    }    vector<int> rightSideView(TreeNode *root){        vector<int> res;        queue<TreeNode*> q;        q.push(root);        while(!q.empty()){            int size = q.size();            while(size--){                TreeNode *temp = q.front();                q.pop();                if(temp->left)                    q.push(temp->left);                if(temp->right)                    q.push(temp->right);                if(size == 0)                    res.push_back(temp->val);            }        }        return res;    }    vector<int> solve(vector<int>& xianxu, vector<int>& zhongxu) {        // write code here        vector<int> res;        if(xianxu.size() == 0)return res;        for(int i=0; i<xianxu.size(); i++)index[zhongxu[i]] =i;        TreeNode* root= buildTree(xianxu, 0, xianxu.size()-1, zhongxu, 0, zhongxu .size()-1);        return rightSideView(root);    }};