学习左神数据结构与算法时做的笔记，由于还没刷完牛客网代码，所以还没放代码上来。

图

分为单向和双向，相邻和不相邻，有数值距离和没有

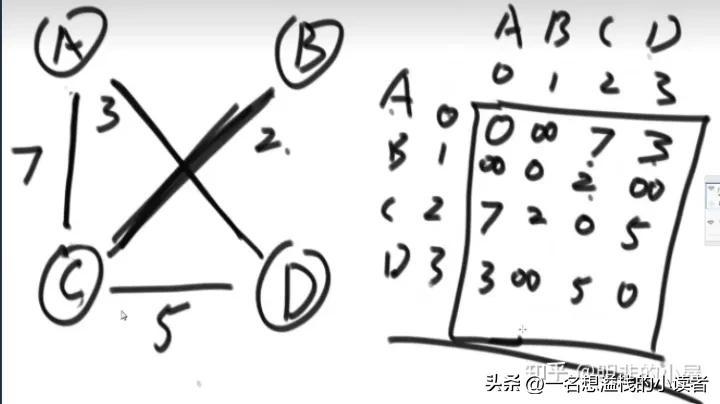
到自己的距离是0，没有相邻是正无穷

可以有很多方式表达图结构，使用一种自己最擅长的方式，把图转化为这种形式去完成问题

图的宽度优先遍历

和二叉树不一样，图可能会有环

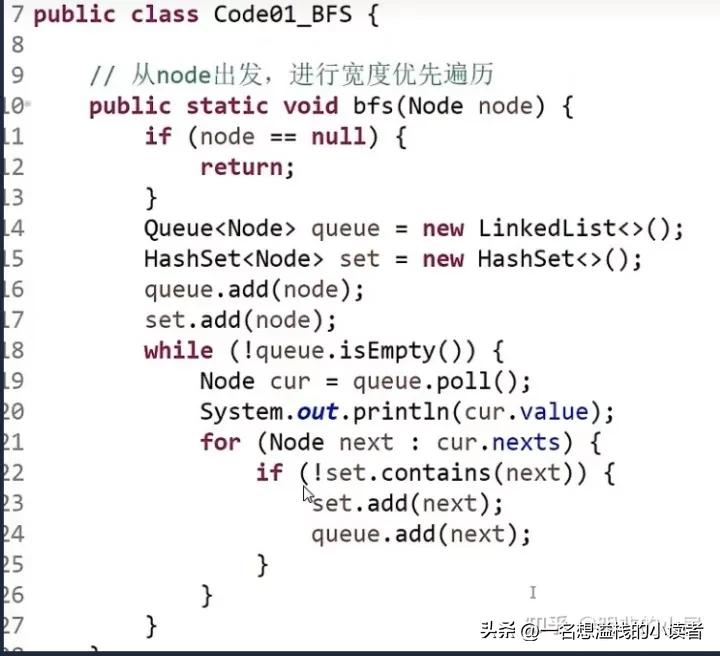
不重复遍历，遇到节点就放入队列和表，当每遇到一个没有在表里的值，加入队列和表，每次弹出队列的值就加入连接的下一个值，检查下一个值是否在表里

深度优先遍历

用栈实现，遇到一个结点，放入栈和表，如果栈不为空，则弹出

弹出遇到有下一个节点，如果不在表里，则把当前结点重新压回栈，而且把下一个节点也压入，记录到表

本质在于每次入下一个节点都是break之后的，一条路走到黑然后才换

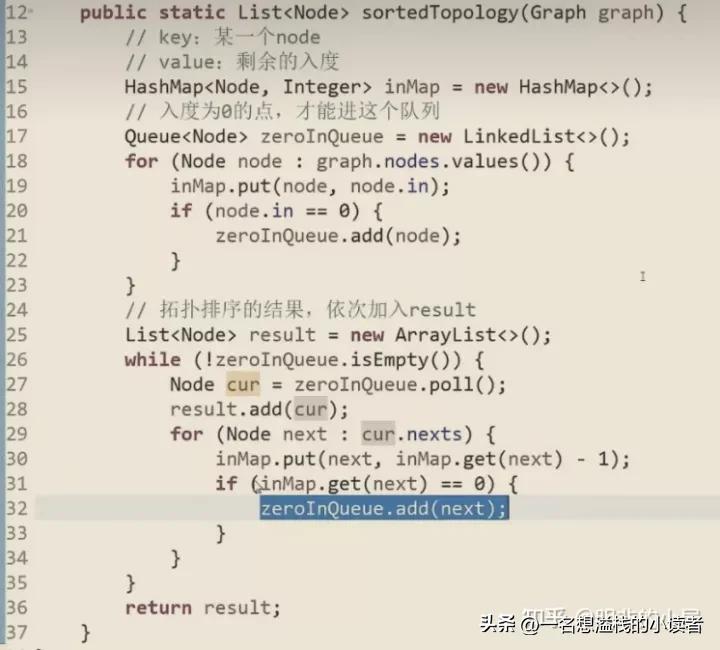
拓扑排序算法

有先后关系，只有没有入度即没有受其他点影响的节点才能弹出

擦除第一个点后，还要清除它所带来的的影响，这么做之后总有下一个不受没有入度的节点，记录该结点

K算法（无向图）

生成最小生成树

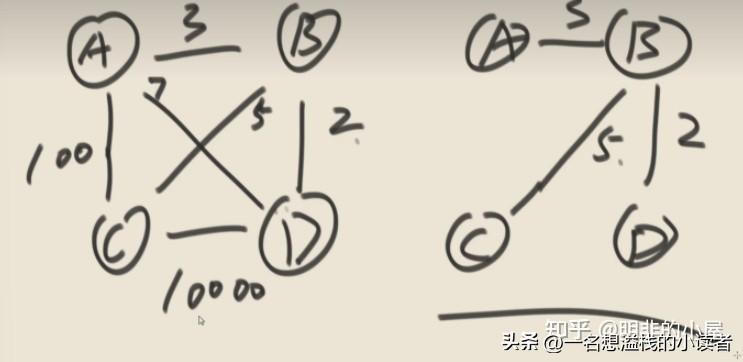
能连通，而且连通之后权值最小

判断会不会形成环是这个问题的关键，可以把每个结点变成集合

当两点成为一条边时，二者形成一个集合，如果不是就可以形成边，合成集合

P算法

从任意点开始入栈，找权值最小的边开始，下一个结点入栈，其余被标记的边表示有存在，下一个节点也是如此，一直从存在的边中找最小

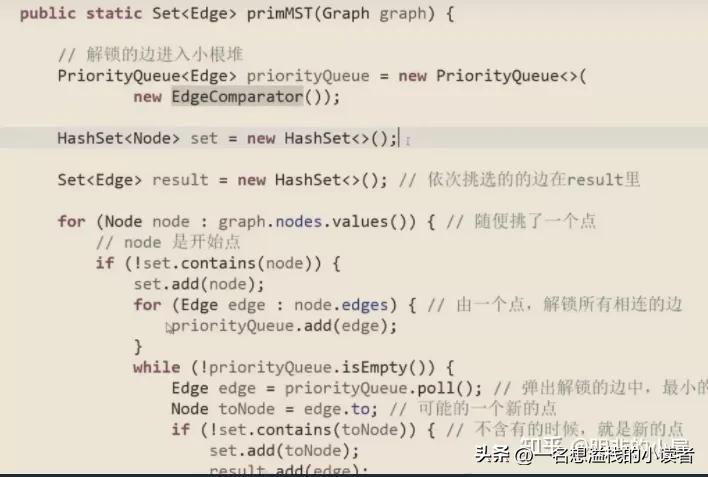
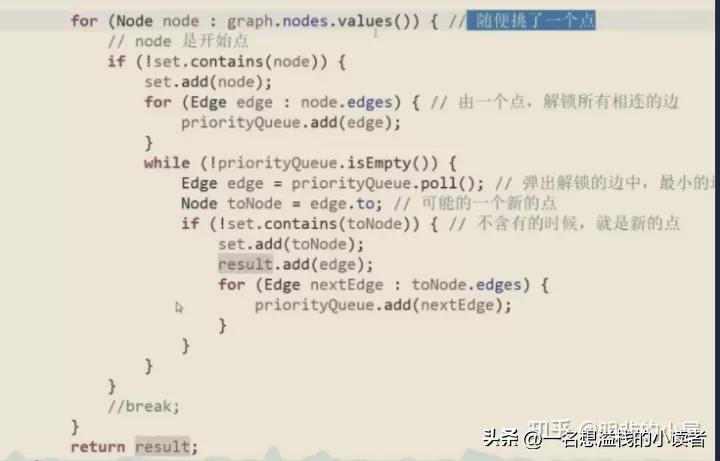
会出现放入重复边的情况，但是会直接跳过，只选最小的边，不会影响结果

for循环是为了解决森林问题，因为可能会出现一大片不连接的图的问题

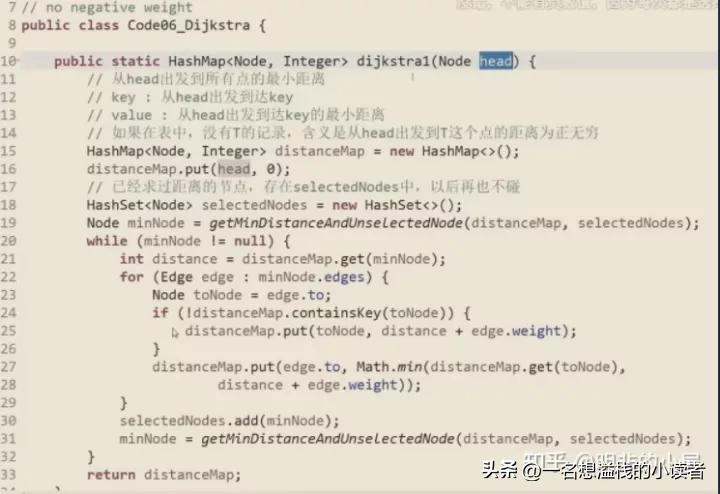
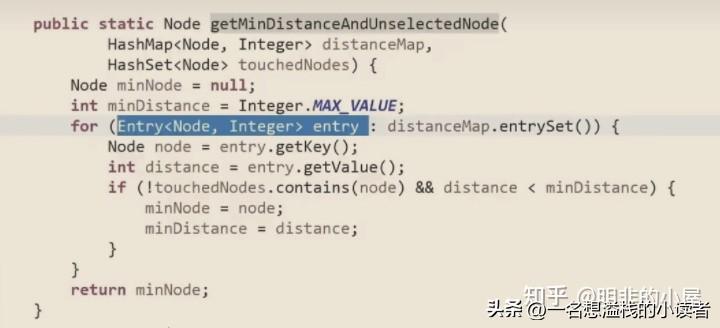
Dijkstra算法

单元最短路径：需要规定出发点，到所有节点的最小距离，到不了就是无穷，没有权值为负数的边（没有累加和为负数的环）

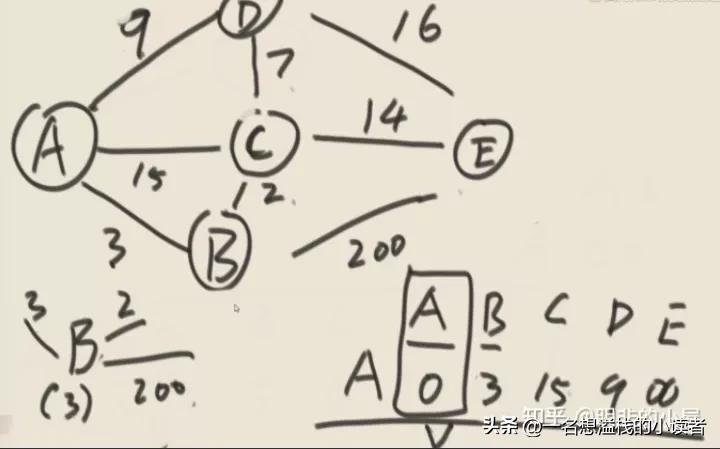
与原本记录的距离对比，更新最小的，到最小之后就把该记录锁死，不变