话不多说，懂得都懂，不想被时代遗忘？不想一再错过机会，算法还不会？两个月后你会感谢现在的选择，跟着博主一起学算法吧。

一、 数据结构和算法内容介绍

1. 字符串匹配问题

最快的速度进行匹配
str=”查德常你好查德你常查德你好”
str= “查德你常查德”
如果让你做，你是不是会用

• 暴力匹配法
  但是如果你会算法你会用
• KMP 部分匹配表

2. 汉诺塔游戏

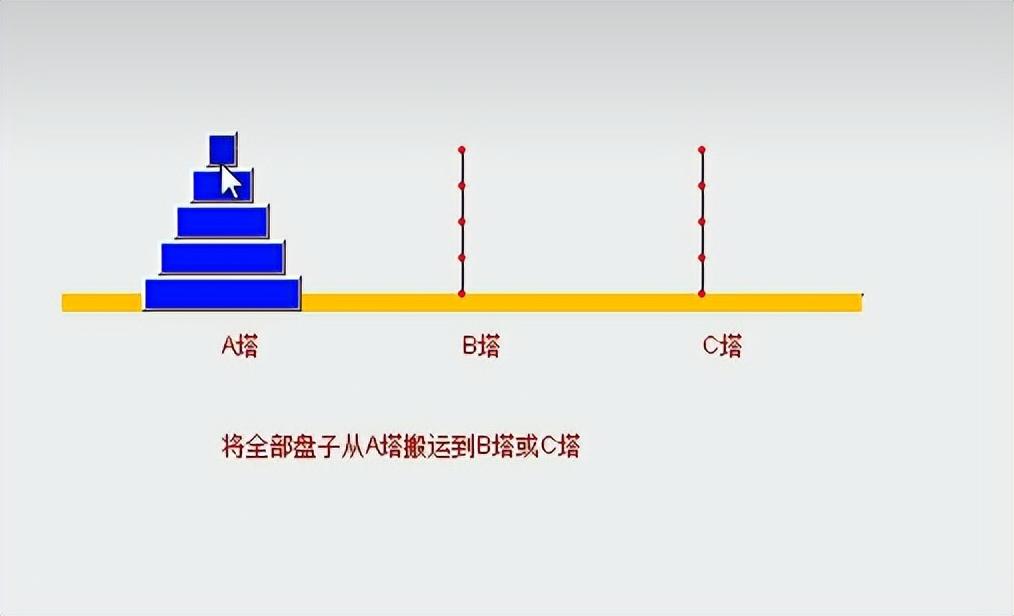
将A 塔的所有圆盘移动到 C 塔，小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘
如果你会算法，你用以下算法会很好解决

• 分治算法

3. 八皇后问题

古老而著名的问题

8*8的棋盘上摆放八个皇后，使其不能互相攻击，即：任意两个皇后不能再同一行，同一列或者统一斜线上，问有多少种摆法

如果你会算法，你用以下算法会很好解决

• 回溯算法

4. 马踏棋盘算法也称骑士周游问题

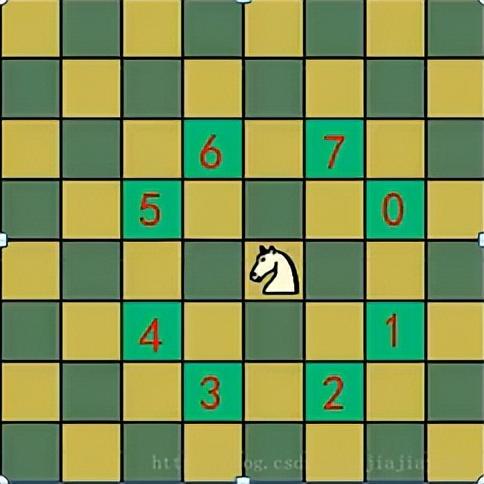
国际象棋8*8的棋盘，马按照日字走，每个方格只走一次，走遍整个棋盘的方格
如果你会算法，你用以下算法会很好解决

深度优化遍历算法（DFS）+贪心算法优化算法是程序的灵魂，优秀的程序在海量数据计算时，依然保持告诉计算。一般情况下内存计算框架（Spark）和缓存技术（比如Rides）来优化程序，思考一下，计算框架和缓存技术，他的核心也是算法。数据结构和算法是公司筛选人才的依据。 程序员门槛越来越高了，不学算法会落伍。

二、数据结构和算法的概述

数据结构是一门研究研究组织数据方式的学科，有了编程语言就有了算法。 数据结构是算法的基础。 程序 = 数据结构 + 算法

实际编程中遇到的问题

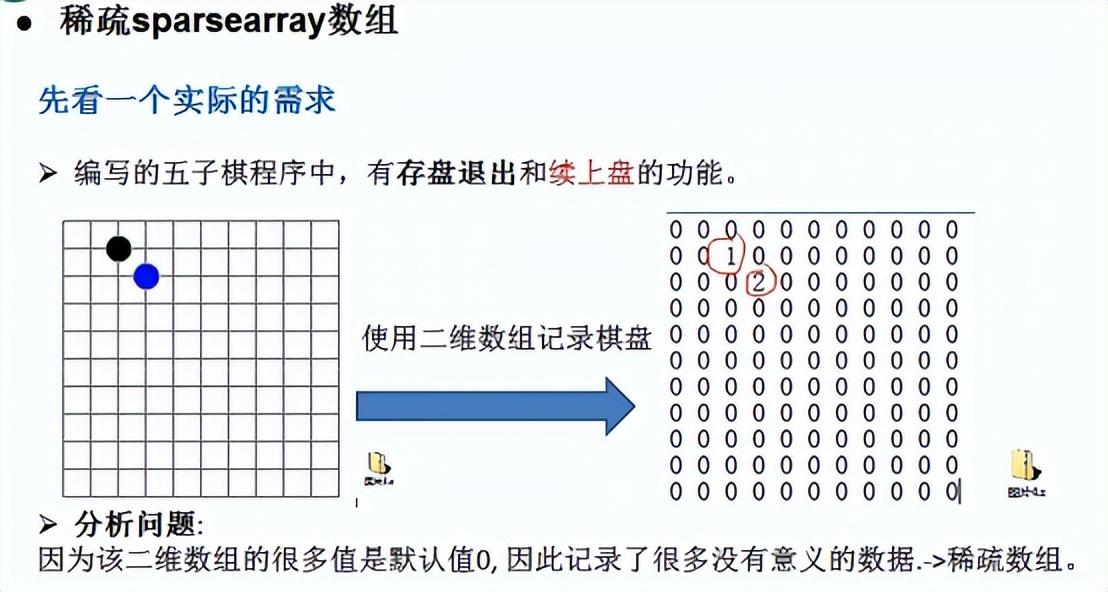
1. 五子棋替换问题

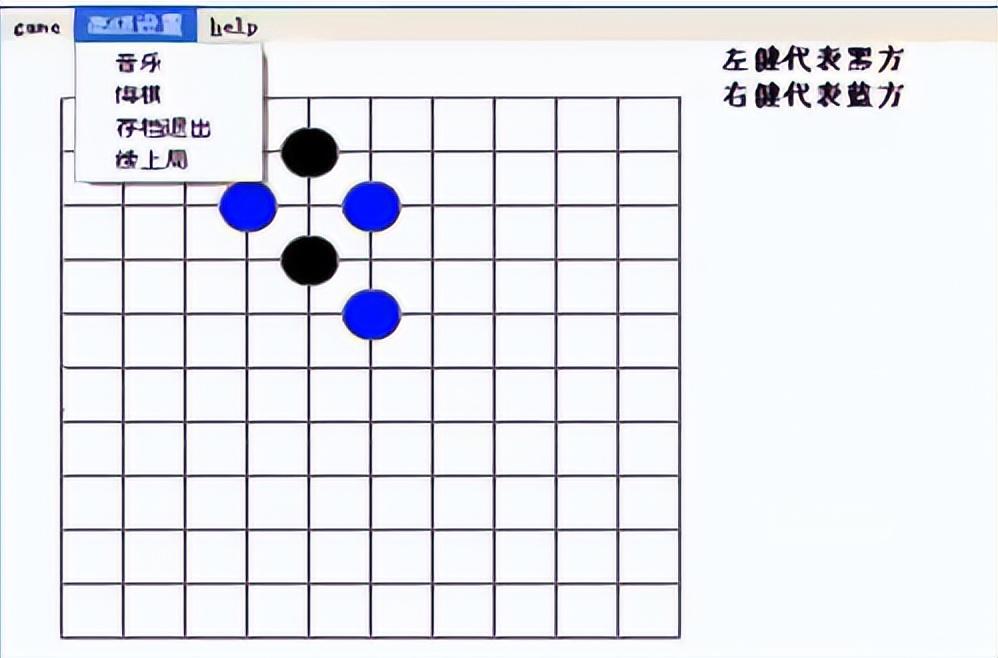
如何判断游戏的输赢，并可以完成存盘推出和继续上局的功能
1）棋盘 二维数组=》（稀疏数组）=》写入文件【存档】
2）读取文件=》稀疏数组=》二维数组=》棋盘【接上局】

数据结构包括：线性结构+非线性结构
线性结构：

存储元素是连续的指的是地址是连续的。

非线性结构：

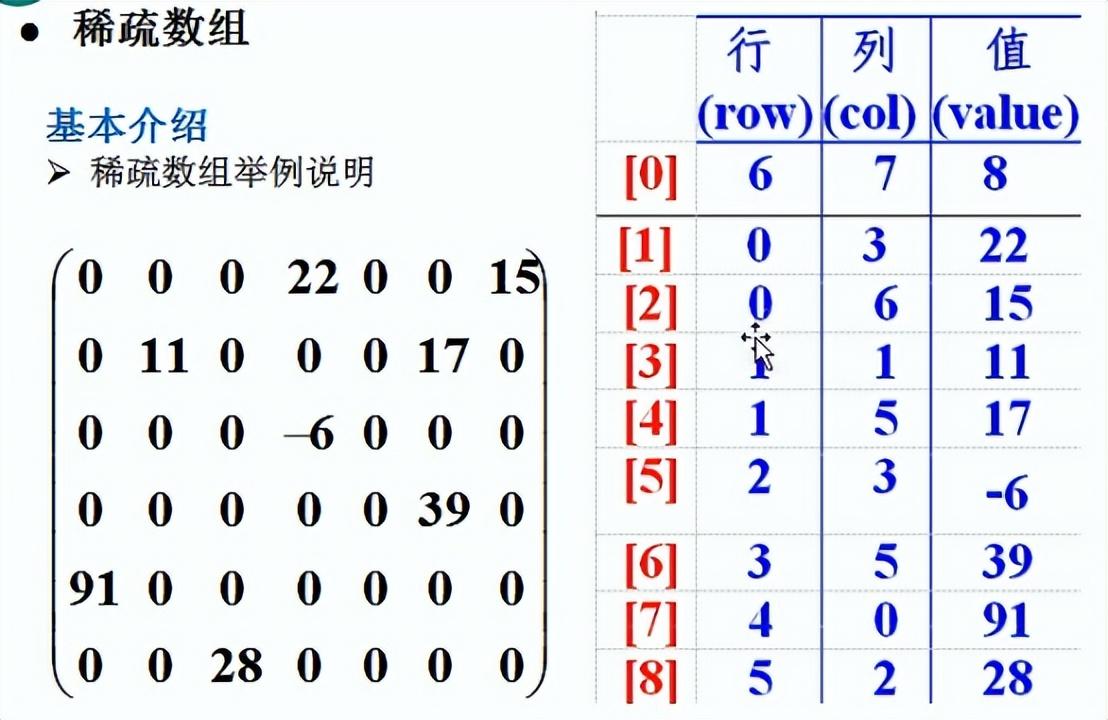
2. 应用场景

从 6 * 7 = 42 个数据
转换为稀疏数组变为 9 * 3 = 27 个数据
起到了使原始数组变小的作用。

3. 应用实例(重点)

1）使用稀疏数组，来保留类似前面的二维数组（棋盘）
2）把稀疏数组存盘，并可以重新回复原来的二维数组
3）整体思路分析

转为稀疏数组的思路
1.遍历原始的二维数组，得到有效数据的个数sum
2.根据个数就可以创建稀疏数组的spareArr int[sum+1][3]
3.将二维数组的有效数据存入到稀疏数组中

恢复的思路
1.先读取第一行根据第一行的数据创建原始的二维数组chessArr2=int[11][11]
2.再其他数据赋值给原始的二维数组即可

代码实现：
创建原始的棋盘，二维数组

public class sparseArr {    public static void main(String[] args) {        int chessArr1[][] = new int[11][11];        chessArr1[1][2] = 1;        chessArr1[2][3] = 2;        System.out.println("原始的二维数组");        for (int[] row: chessArr1) {            for (int data: row) {                System.out.printf("%d\t",data);            }            System.out.println();        }    }}

结果：

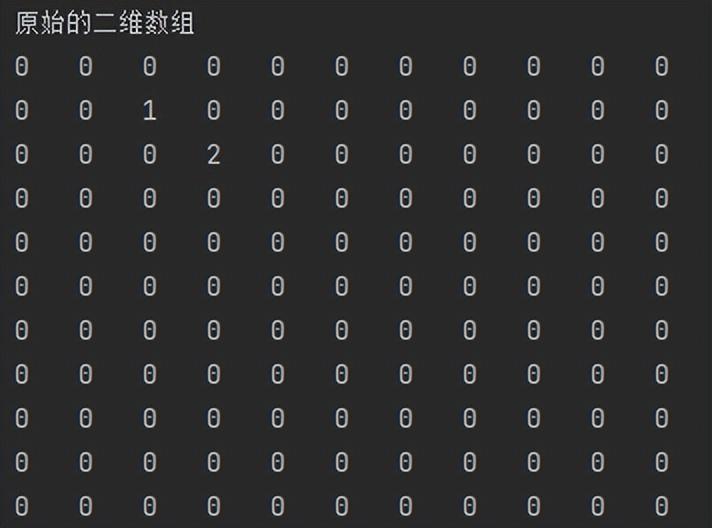
求sum,一共有多少非零个数

int sum = 0;for (int i = 0; i < chessArr1.length; i++){    for (int j = 0; j < chessArr1.length; j++) {        if(chessArr1[i][j]!=0){sum++;}    }}System.out.println(sum);

得出结果2

创建稀疏数组并赋值

int sparseArr[][] = new int[sum+1][3];//给稀疏数组赋值sparseArr[0][0] = 11;sparseArr[0][1] = 11;sparseArr[0][2] = sum;int count = 0;for (int i = 0; i < chessArr1.length; i++){    for (int j = 0; j < chessArr1.length; j++) {        if(chessArr1[i][j]!=0){            count++;            sparseArr[count][0] = i;            sparseArr[count][1] = j;            sparseArr[count][2] = chessArr1[i][j];        }    }}for(int[] row: sparseArr){    for (int data : row){        System.out.printf("%d\t",data);    }    System.out.println();}

得到稀疏数组

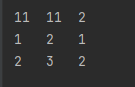
将稀疏数组恢复成原始的数组（棋盘）

重新创建二维数组（棋盘）chessArr2

int[][] chessArr2 = new int[sparseArr[0][0]][sparseArr[0][1]];int rowNum = 0;//已知稀疏数组有3列for (int[] row: sparseArr) {    rowNum++;}for(int i = 1; i < rowNum; i++){    chessArr2[sparseArr[i][0]][sparseArr[i][1]]=sparseArr[i][2];}for (int[] row: chessArr2){    for (int data: row){        System.out.printf("%d\t",data);    }    System.out.println();}

运行结果

可以看出二维数组可以极大的节省我们的存储空间