数据结构与算法的基本原理解析

一、算法及其描述

1、算法是对特定问题求解步骤的一种描述，它是指令的有限序列。

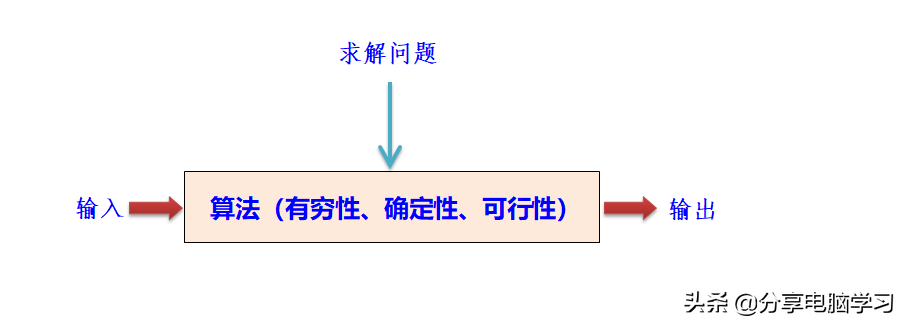
2、算法具有以下五个重要的特性

（1）有穷性。指算法在执行有限的步骤之后，自动结束而不会出现无限循环，并且每一个步骤在可接受的时间内完成。

（2）确定性。对于每种情况下执行的操作，在算法中都有确定的含义，不会出现二义性。并且在任何条件下，算法都只有一条执行路径。

（3）可行性。算法的每条指令都是可执行的，即便人借助纸和笔都可以完成。

（4）输入性。算法有零个或多个输入。大多数算法中输入参数是必要的，但对于较简单的算法，如计算1+2的值，不需要任何输入参数，因此算法的输入可以是零个。

（5）输出性。算法至少有一个或多个输出。算法用于某种数据处理，如果没有输出，这样的算法是没有意义的，算法的输出是和输入有着某些特定关系的量。

练习：用擅长的语言编写以下案例

3、算法描述

通常算法用一个或者几个函数（或者方法）描述

（1）函数的返回值通常为布尔类型，表示算法是否成功执行。在有些情况下可以直接用算法的返回值来区分输入参数的正确性。

（2）形参列表表示算法的参数，由输入参数和输出参数构成。

（3）函数体实现算法的功能。

练习：求和问题是当n≥1时求s=1+2+…+n。

输入参数为n，操作结果为s。

初始条件是n≥1。

当初始条件不满足，返回False，否则计算出s并返回True。

二、算法分析

1、算法的设计目标

正确性。

可使用性。

可读性。

健壮性。

高时间性能与低存储量需求。

2、算法分析目的：分析算法的时空效率以便改进算法性能。

3、算法时间性能分析

（1）算法分析方式：

事后分析统计方法：编写算法对应程序，统计其执行时间。

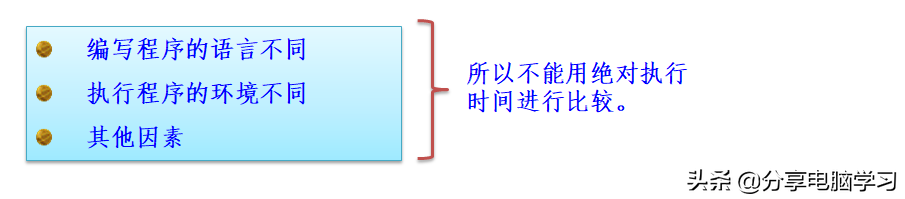
事前估算分析方法：撇开上述因素，认为算法的执行时间是问题规模n的函数。

（2）分析算法的时间复杂度

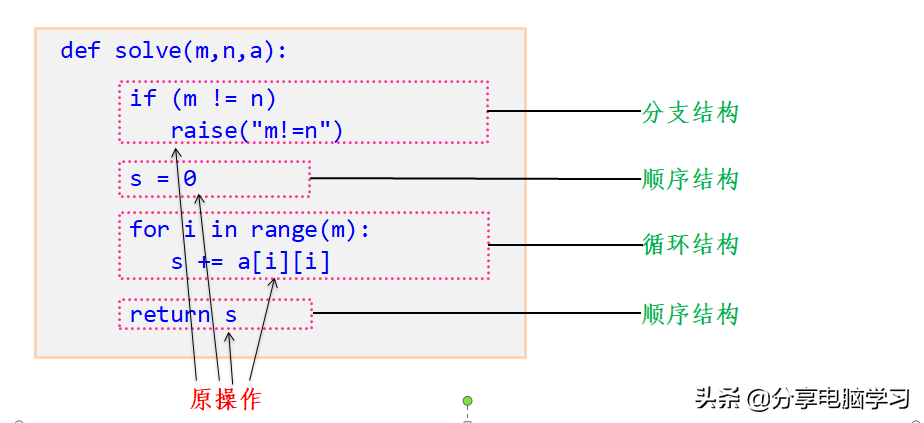
一个算法是由控制结构（顺序、分支和循环三种）和原操作（指固有数据类型的操作，如+、-、*、/、++和--等）构成的。算法执行时间取决于两者的综合效果。

算法的执行时间取决于控制结构和原操作的综合效果。

在一个算法中，执行原操作的次数越少，其执行时间也就相对地越少；执行原操作次数越多，其执行时间也就相对地越多。

算法中所有原操作的执行次数称为算法频度，这样一个算法的执行时间可以由算法频度来计量。

（3）计算算法频度T(n)

假设算法的问题规模为n，例如对10个整数排序，问题规模为n就是10。算法频度是问题规模n的函数，用T(n)表示。

算法执行时间大致等于原操作所需的时间×T(n)，也就是说T(n)与算法的执行时间成正比。为此用T(n)表示算法的执行时间。比较不同算法的T(n)大小得出算法执行时间的好坏。

（4）T(n)采用时间复杂度表示

算法中执行时间T(n)是问题规模n的某个函数f(n)，记作：

(n) = O(f(n))

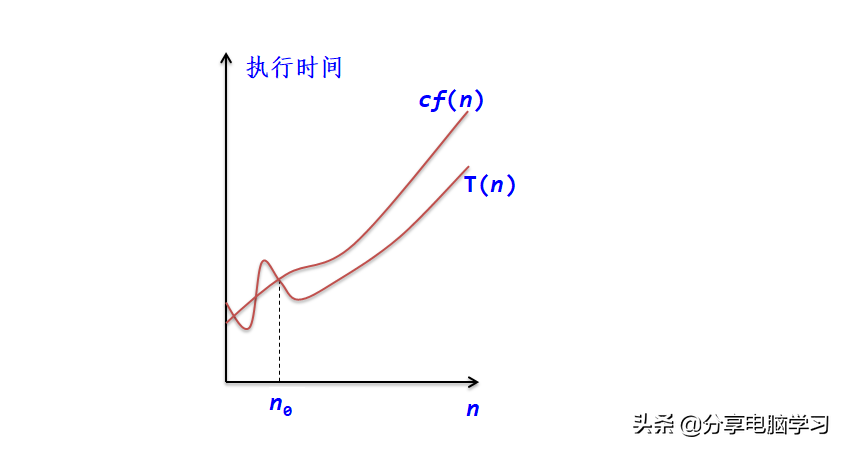
"O"的形式定义为：

T(n) = O(f(n))表示存在一个正的常数c，使得当n≥n0时都满足：|T(n)|≤c|f(n)|

f(n)是T(n)的上界，这种上界可能很多，通常取最接近的上界，即紧凑上界

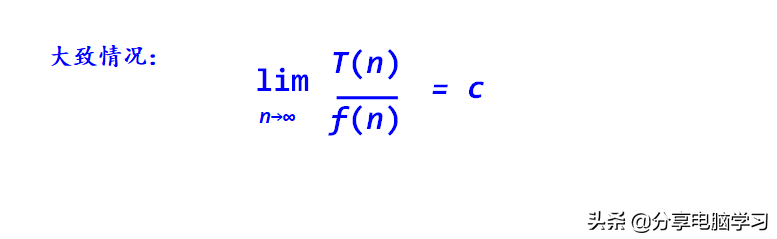
提示：就是只求出T(n)的最高阶，忽略其低阶项和常系数，这样既可简化T(n)的计算，又能比较客观地反映出当n很大时算法的时间性能。本质上讲是一种T(n)最高数量级的比较。

一般地：

各种不同算法时间复杂度的比较关系如下：

例子：

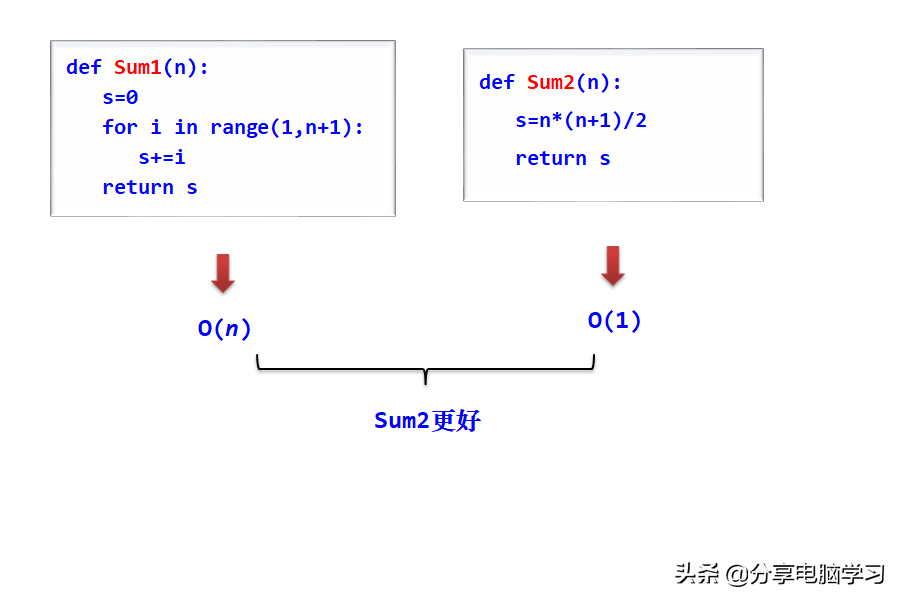
（5）简化的算法时间复杂度分析

一种简化的算法时间复杂度分析方法是，仅仅考虑算法中的基本操作。

所谓基本操作是指算法中最深层循环内的原操作。而算法执行时间大致等于基本操作所需的时间×其运算次数。所以在算法分析时，计算T(n)时仅仅考虑基本操作的执行次数。

例子

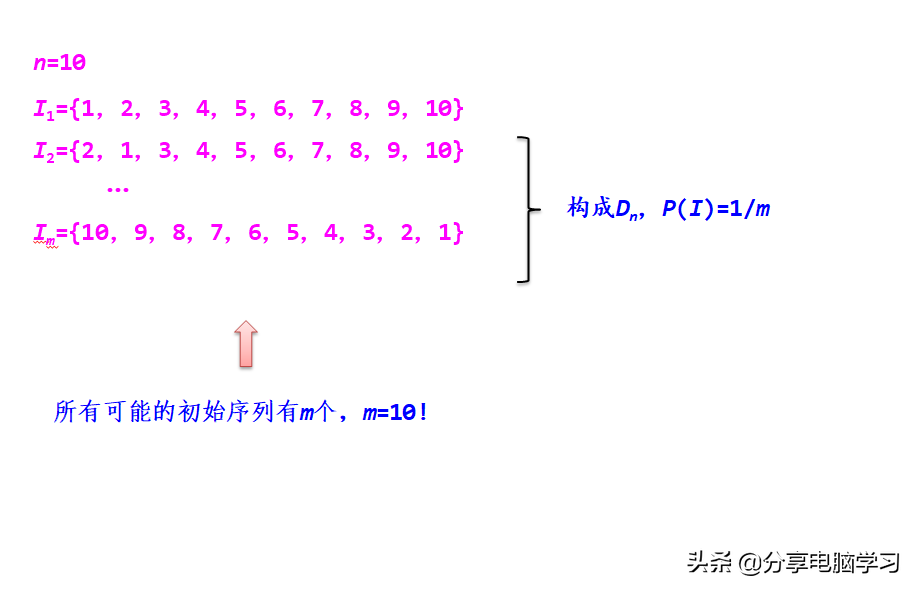
（5）算法的最好、最坏和平均时间复杂度

例如，10个1～10的整数序列递增排序：

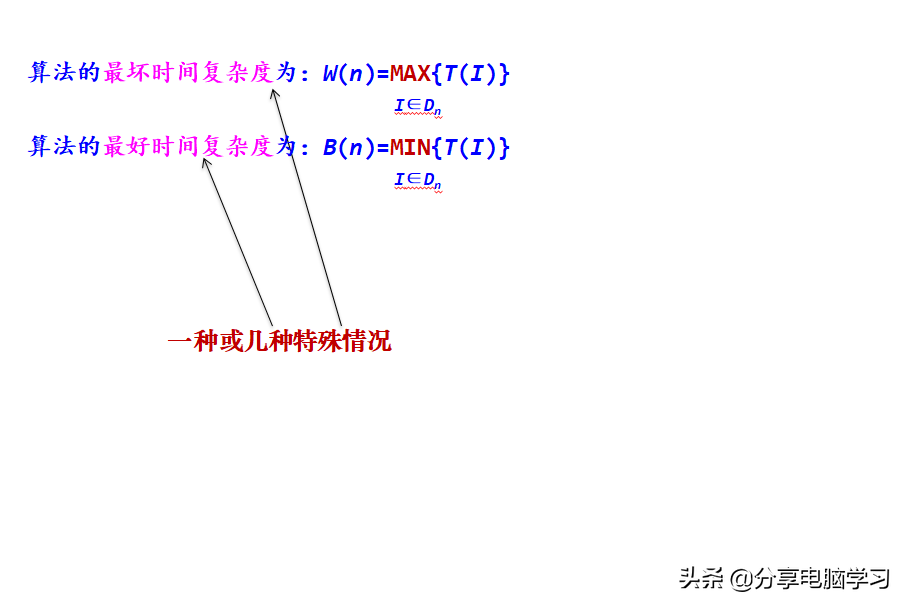
注：

算法时间性能比较：假如求同一问题有两个算法：A和B，如果算法A的平均时间复杂度为O(n)，而算法B的平均时间复杂度为O(n2)。

一般情况下，认为算法A的时间性能好比算法B。

练习：

该算法的主要时间花费在元素比较上，可以将元素比较看成基本操作。

（1） 算法在查找中总是从i=0开始的，如果a[0]=k，则仅仅一次比较就成功找到k，呈现最好情况，所以算法的最好时间复杂度为O(1)。

（2） 如果a[n-1]=k，则需要n次比较成功找到k，呈现最坏情况，所以算法的最坏时间复杂度为O(n)。

（3） 考虑平均情况：

a[0]=k时比较1次

a[1]=k时比较2次

…

a[n-1]=k时比较n次

共n种情况，假设等概率，也就是说每种情况的概率为1/n，则平均比较次数=(1+2+…+n)/n=(n+1)/2=O(n)，所以算法平均时间复杂度为O(n)。

（3）算法空间性能分析

一个算法的存储量包括形参所占空间和临时变量所占空间。在对算法进行存储空间分析时，只考察临时变量所占空间。

空间复杂度是对一个算法在运行过程中临时占用的存储空间大小的量度，一般也作为问题规模n的函数，以数量级形式给出，记作：S(n)=O(g(n))。

其中"O"的含义与时间复杂度分析中的相同。

为什么算法空间分析只考虑临时空间，而不必考虑形参的空间呢？

分析算法的空间复杂度

三、数据结构的目标

1、好算法设计的过程

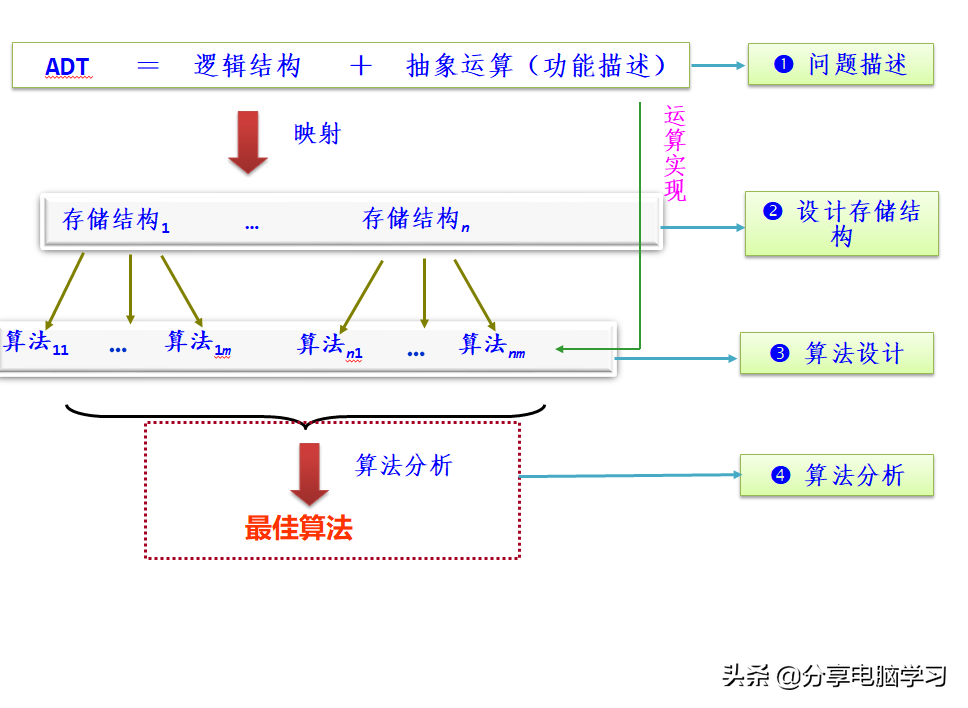
采用面向对象的程序设计语言实现抽象数据类型时，通常将一个抽象数据类型设计成一个类，采用类的数据变量表示数据的存储结构，将抽象运算通过类的公有方法实现。

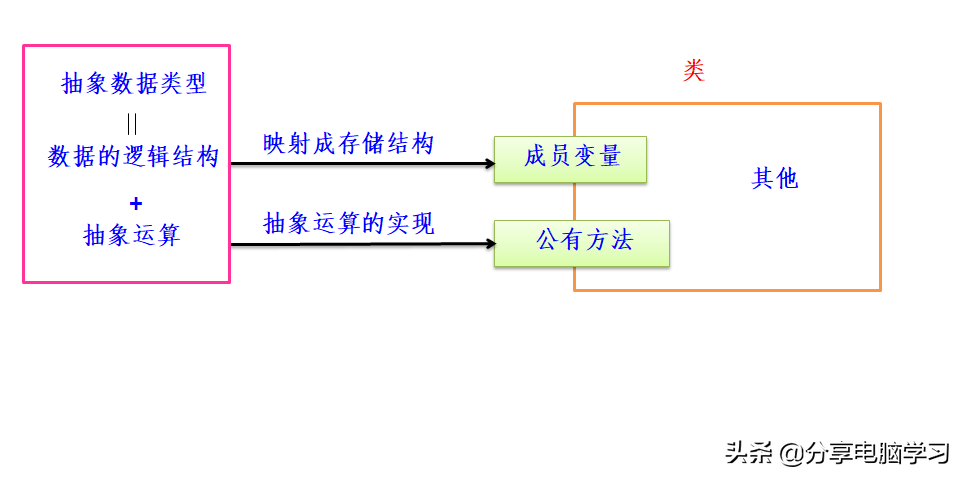
2、存储结构对算法的影响主要在两方面：

存储结构的存储能力

存储结构应与所选择的算法相适应

3、例子

构造集合ADT Set，假设其中元素为整型，遵循标准数学定义，基本运算包括:

求集合长度、求第i个元素、判断一个元素是否属于集合、向集合中添加一个元素、从集合中删除一个元素、复制集合和输出集合中所有元素。

另外增加3个集合运算:

求两个集合并Union、集合交Inter和集合差Diff。

设计存储结构

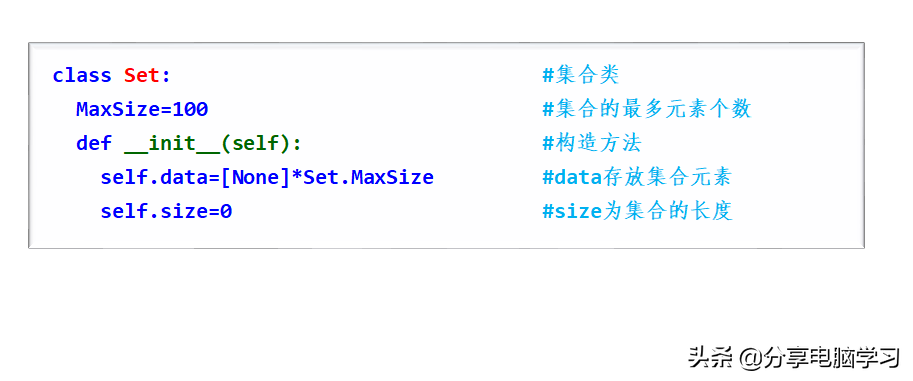
设计运算算法

Set类包含以下基本运算方法：

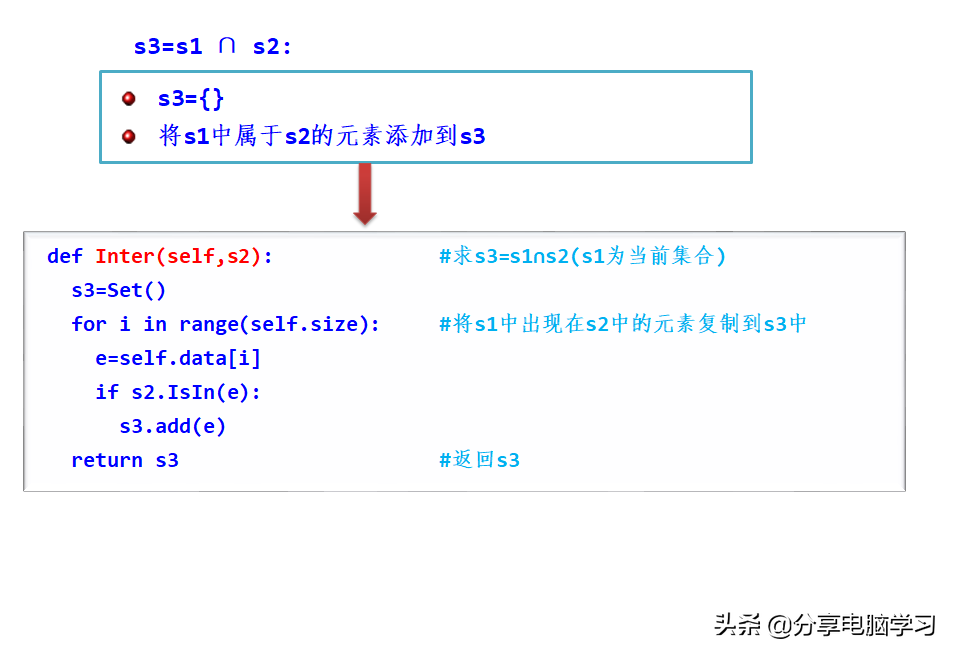
设计主程序