图论初探：数据结构与算法的深度解析

图的元素叫作 顶点 ，顶点间的连接关系叫做 边 ，跟顶点相连的边的条数称为 顶点的度

​ 图根据是否有方向可分为 有向图 和 无向图 ，有向图的边有方向，度也分为 入度 (指向顶点的边的个数)和 出度 (顶点指向的边的个数)

​ 有权重的图称为 带权图 ，也就是边有权值

​ 用图展示下(左上无权无向图、右上无权有向图、左下有权无向图、右下有权有向图)：

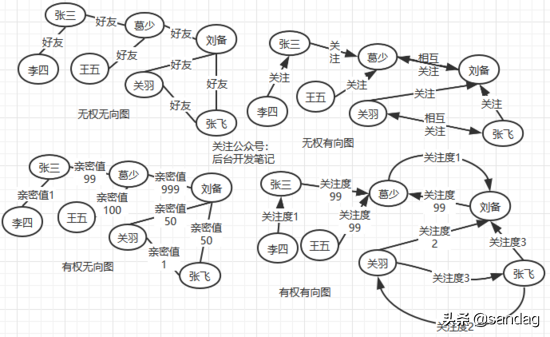
存储方式

​ 图的存储方式有两种，一种是 邻接矩阵 ，另一种是 邻接表

​ 邻接矩阵实质是n×n的二维数组 ， m[i][j] 在无权无向图中代表是否连接， m[i][j] 在无权有向图中代表i是否单向连接j， m[i][j] 在有权无向图中代表是否i和j的连接权重， m[i][j] 在有权有向图中代表i单向连接j的权重

​ 优点是存储方式简单，查询高效，缺点是当点多边少时，邻接矩阵易造成内存空间浪费，以有向有权图为例：

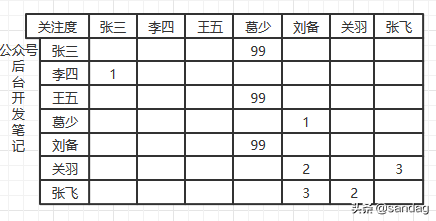
​ 邻接表实质就是一组动态数组(或链表、红黑树、跳表、散列表等)，优点是内存占用少，缺点就是查询相比邻接矩阵低(有序动态数组可以二分查找，红黑树、跳表、散列表相比链表也快很多)，以有向有权图用邻接表(链表形式)为例：

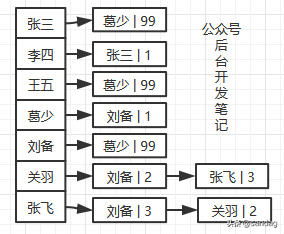
拓扑排序

​ 让有向无环图中所有顶点排成一个 线性序列 ，使图中 任意 一对顶点u和v，若点u到v连通， 都 满足在线性序列中u位于v前。有两种实现方法，分别是 Kahn算法 和 DFS

​ 它可用于检测 图中是否存在环 、 还可以通过 局部顺序来推导全局顺序 (比如用于处理编译文件的依赖项)

Kahn算法

​ 实质上是贪心算法。如果某个顶点 入度为 0 ，就表示没有任何顶点必须先于这个顶点执行，那么这个顶点就可以执行了。

​ 因此我们先从图中找出一个入度为 0 的顶点并输出，然后把这个顶点从图中删除（把这个顶点可达的顶点的入度都减 1）。循环执行上面的过程直到所有的顶点都被输出

伪代码：

void Kahn() {  for (int i = 0; i < v; ++i) {    for (int j = 0; j < vec[i].size(); ++j) {      int w = vec[i][j]; //说明存在i->w      num[w]++;			//统计节点的入度    }  }  //先把入度为0的节点加入队列  for (int i = 0; i < v; ++i) {    if (num[i] == 0) queue.push(i);  }  //循环执行：输出入度为0的节点，并把该节点指向的节点入度--，若指向节点入度变为0则加入队列  while (!queue.isEmpty()) {    int i = queue.pop();    printf("->%d", i);    for (int j = 0; j < vec[i].size(); ++j) {      int k = vec[i][j];      num[k]--;      if (num[k] == 0) queue.push(k);    }  }}复制代码

DFS算法

​ 先 通过邻接表构造逆邻接表 ，再 递归处理每个顶点 (对于一个顶点先输出可达它的所有顶点，再输出自己)

伪代码：

void Topology() {  for (int i = 0; i < v; ++i) { // 通过邻接表生成逆邻接表    for (int j = 0; j < vec[i].size(); ++j) {      int w = vec[i][j]; // i->w      vecRotate[w].push(i); // w->i    }  }  for (int i = 0; i < v; ++i) { // 深度优先遍历图    if (visited[i] == false) {	// 未标记走过的进行dfs      visited[i] = true;	      dfs(i);    }  }}void dfs(int v) {  for (int i = 0; i < vecRotate[v].size(); ++i) {    int w = vecRotate[v][i];    if (visited[w] == true) continue;	//若指向v的节点w已经标记过就跳过    visited[w] = true;					//否则就标记先dfs输出w    dfs(w);  }  //先输出可达它的所有顶点，再输出自己  printf("->%d", v);}

单源最短路

​ 用于求 一个顶点到一个顶点 的最短距离，最常见的算法为dijkstra算法，时间复杂度为O(E × logV)E为边数，V为顶点个数，具体做法是：

​ 用 v 数组记录起点到每个点的距离 (初始化无穷大)，然后把起始顶点初始化为 0 并放入 优先级队列

​ 每次从优先级队列取出 距离最小 的顶点p，若 p可直达q，且v[p]+p到q距离 < v[q] ，就更新 v[q]=v[p]+p到q距离 ，并把q加入到优先级队列，重复该过程直到找到终止或队空

​ 除此之外， predecessor数组记录每个顶点的前驱 ，用于 还原最短路径 ； inqueue数组判定顶点是否已经在优先队列中 ， 避免重复添加 ， m数组记录相邻节点+距离

​ 具体流程图：

伪代码

void dijkstra(int s, int t) { 	//获取s->t的最短路径  //step1:先初始化s到所有节点的距离无穷大  for (int i = 1; i <= n; i++) {      v[i].id = i;      v[i].dist = INF;  }  //step2：再将到s节点(它本身)的距离初始化为0，并加入到优先队列  v[s].dist = 0;  queue.push(v[s]);  inqueue[s] = true;  //循环执行  while (!queue.isEmpty()) {    minVertex = queue.pop(); //从优先级队列取出距离最小的顶点minVertex    if (minVertex.id == t) break; 	// 找到终点直接跳出    //查找所有与距离最小节点相连的顶点    for (int i = 0; i < m[minVertex.id].size(); ++i) {      int tempDist = m[minVertex.id][i].dist;       int e = m[minVertex.id][i].id;      //若minVertex可直达e，且v[minVertex]+minVertex到e距离<v[e]      if (minVertex.dist + tempDist < v[e].dist) {        //就更新v[e]=v[minVertex]+minVertex到e距离        v[e].dist = minVertex.dist + tempDist;        predecessor[v[e].id] = minVertex.id;        //并把e加入到优先级队列(若e已经在优先队列中，则直接修改)        if (inqueue[v[e].id] == true) {          queue.update(v[e].dist);      // 更新队列中的 dist 值        } else {          queue.push(v[e]);          inqueue[v[e].id] = true;        }      }    }  }  // 输出最短路径  printf(s);  print(s, t);}//根据前驱递归输出路径void print(int s, int t) {  if (s == t) return;  print(s, predecessor[t]);  printf("->%d", t);}

应用场景

​ 除了应用于 地图求最短路 外，还可应用于 求前k优组合 ，例如翻译一个句子，句中有3个单词，每个单词都有 一组可选的翻译列表并针对每个翻译打分，我们从每个单词的翻译列表中选择一个，组合起来就能得到句子的整体翻译，求前k高分的翻译结果：

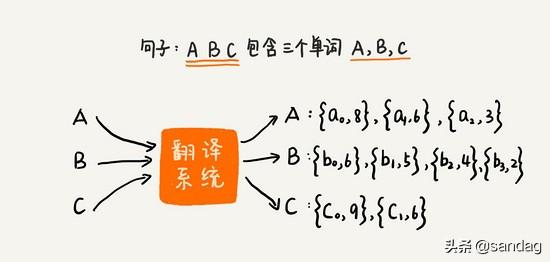
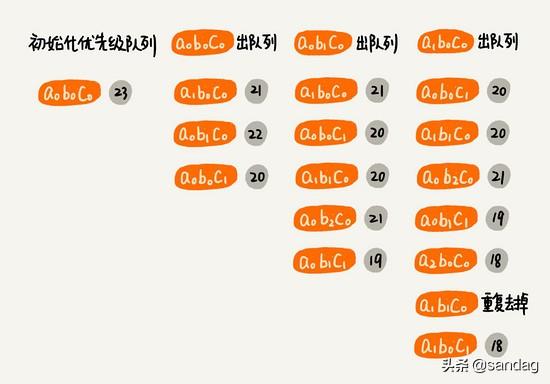
​ 对此，我们可以把每个单词可选翻译列表按高到低排序，然后将最高分 a0b0c0 放入优先队列。

​ 每次从优先级队列取出得分最高的组合，并基于这个组合进行扩展(扩展策略是每个单词的翻译分别替换成下一个单词的翻译)，重复这个过程直到取出k个为止，流程图为：