人工智能在IMO赛场上的惊人突破

近日，DeepMind的AlphaProof/AlphaGeo在国际数学奥林匹克竞赛(IMO)中取得了前所未有的成绩，解出了六道问题中的四道获得银牌。这一成就无疑将与“深蓝”击败卡斯帕罗夫和“AlphaGo”击败李世石一样，成为人工智能挑战人类智力巅峰的又一里程碑，同时也将引发新一轮关于机器智力边界的讨论。

早期发现和培养数学天才的重要性已经被很多人认可，他们提出了一个颠覆性的数学教育理念——将前沿科学研究转化为不需要专业知识背景的抽象基础数学问题，用这些问题在更小年龄段选拔科研人才。在这种思路下，分子结构，线性规划等复杂的科学问题被简化为如鸡兔同笼、牛吃草等基础数学题。与传统注重知识点的教育模式相比，奥数更考验包括归纳和推理能力在内的“流动智力”。奥数解题过程更接近科研工作的本质——将具体问题抽象化，或将抽象问题具体化，然后在不同抽象层级间穿梭。这种教育理念在选拔数学人才方面取得了卓越成功——许多IMO参赛者后来成为杰出数学家，其中16名奖牌得主更是获得了数学界最高荣誉菲尔兹奖。

奥数题目注重通用逻辑能力的特点，使其成为衡量人工智能逻辑能力的理想工具。与大多数针对特定知识点和基本逻辑判断的人工智能基准测试不同，奥数可以通过多重逻辑推理和难以穷举的考核方式来评估人工智能的能力。这意味着最有效的解题方法不是简单的“背题”式预训练，而是运用通用推理方法——这也是人类在奥数中取得优异成绩和进行科研工作所需的核心能力。

AlphaProof/AlphaGeo在国际奥数比赛中获得银牌，仅次于54名金牌选手，标志着人工智能系统在通用推理能力上的进步。与“深蓝”和“AlphaGo”击败人类顶尖选手不同，奥数涵盖的领域更加广泛，对创造性思维和解决前所未见问题的能力要求更高，同时对论证的严谨性要求极为苛刻。这些特点让我们看到了人工智能在科研工作中取代人类的巨大潜力。

人工智能在国际奥数比赛上的突破主要源于三大创新：神经/符号双系统架构，人造数据训练方法，探索式举一反三。

神经/符号双系统架构巧妙地结合了神经网络和符号系统的优势。神经网络基于深度学习模型，具有强大的归纳能力，可从海量数据中发现隐藏规律。虽然它可能产生“幻觉”，但这种“创造力”对突破常规思维很有价值。与之互补的符号系统则擅长严谨的逻辑推理，能在逻辑框架内做出准确判断。DeepMind将这两个系统融合，创造出一种独特的问题解决方法。

目前，数学界最受关注的机器命题证明系统是Lean语言，这也是IMO主办者提供给人工智能的题目格式。首先，它将题目转换为机器可读的Lean命题，让符号系统进行逻辑推导，得出更多命题。如果这还不足以解决问题，神经网络就会介入，运用“扩散性思维”（基于蒙特卡洛树搜索）寻找可能正确的中间命题，搭建已知条件和待证明结论之间的桥梁。经过大量训练，神经网络在寻找关键推理步骤方面变得越来越高效。

第二个突破是采用“人造数据”方法创建训练集。符号引擎生成了数十亿级的奥数题，这些题目虽然缺乏实际比赛题目的巧妙性，但正确性有保证。通过隐藏中间步骤，这些题目需要神经网络和符号系统协作来解决。训练过程重点关注需要神经系统参与的蒙特卡洛树搜索步骤，提升了模型预判关键推理环节的能力。虽然这些人造题目与实际比赛题目有所不同——后者更注重巧妙和独特的解法，而非通用方法——但由于数据量庞大，许多经典证明方法也被随机生成，在丰富了模型的知识库的同时也验证了模型和人类推理的互通之处。

第三个突破是搜索和验证个例的人工智能模块。DeepMind与多位数学家在《自然》杂志上发表的研究阐述了深度学习模型在前沿数学中的潜在应用，其中搜索和验证个例的方法在AlphaProof中得到验证。数学家的工作过程与模型相似，包含“扩散式探索”和严谨论证两个部分。对于一个命题，数学家首先创造个例，然后严格验证命题在个例中的正确性。如果发现不正确，他们需要凭直觉改进命题，排除错误个例，再继续验证。“创造个例”和“验证个例”由符号引擎完成，而改进命题则由扩散式神经网络负责。如果引擎能创造足够多的个例，神经网络就能从这些数据中的规律判断出更可能正确的命题。DeepMind介绍了这种拟人工作方式在拓扑学和抽象代数上取得的突破，这些成果得益于深度学习能够发现不明显的、非线性的、需要大量计算的规律。

通过分析本次国际数学奥林匹克竞赛（IMO）各题目的解题表现，我们可以清晰地看到不同算法如何提升和补充了人工智能模型的能力。

Q4作为一道典型的几何题，展示了DeepMind今年早些时候发布的AlphaGeo算法的能力。与更为通用的AlphaProof不同，AlphaGeo专注于通过几何题引擎和辅助线解决几何问题。它通过建立一个包含一亿条复杂命题证明的庞大数据库，培养了神经网络判断辅助线效用的能力。这个理解辅助线功效的神经网络能够从数十条可行的辅助线中筛选出最具潜力的方向。这种高效筛选使AlphaGeo能在搜索树上深入探索，从而解决更具挑战性的问题。由于几何题的搜索空间最小，AlphaGeo在拿到题后19秒就证明出来了，远快于任何人类。(图为AlphaGeo的解法和辅助线)

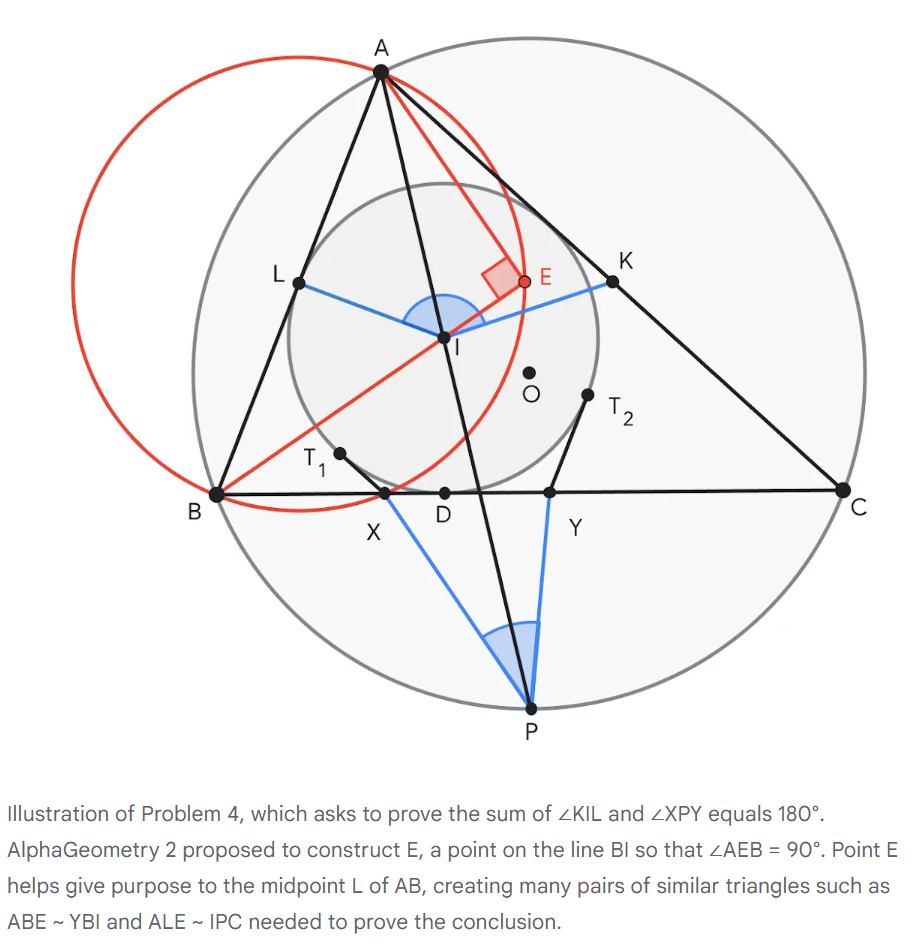
Q2则考验了“中间命题”的广度。与几何题不同，数论问题的中间步骤搜索空间更为广阔。在Q2中，如果参赛者（无论是人类还是AI）能洞察到x=ab+1这个巧妙的中间步骤，整个问题就会简化为仅需三行即可证明的简单命题。这意味着，AlphaProof与人类一样，需要具备发现x=ab+1的洞察力。考虑到这个构造在已知题库中前所未见，对它的洞察力必然源于AlphaProof在生成数十亿训练样本的过程中，反复尝试类似问题后产生的涌现能力。

Q1和Q6则考验了AI反复创造和验证个例的能力。具备这种能力的AI可以基于已知命题生成大量个例，通过验证这些个例是否符合证明条件，不断探索正例和反例的边界，最终找到正确的命题。这种主动探索能力的出现，预示着AI有能力在寻找未知解时探索新颖路径，并在过程中不断调整方向。最令人惊叹的是，在这次比赛中，只有五名人类选手解出的Q6，AlphaProof却给出了满分证明。这有力地证明了AI在某些方面已经超越了人类的通用推理能力。

然而，AI未能解出的Q3和Q5，都属于奥数中的“排列组合”问题。这类问题的特点是解空间极其发散，且命题相对更加开放。这导致AlphaProof在构建人造题库时难以进行更深入的搜索，从而限制了它在这类问题上的解题能力上限。这不仅展示了AI在数学推理方面的巨大进步，也揭示了它在解空间更广的领域存在的局限性，为未来AI算法的改进指明了方向。

人工智能在IMO的成就，为我们展示了人工智能如何助力前沿数学研究。虽然这类模型从狭义上看并非“通用人工智能”——其训练集和用途局限于解决不等式、平面几何、数论等特定题目，但其开发方法为人工智能在高级智力劳动中的应用提供了宝贵启示。IMO模型的成功也指明了未来科研工作者与深度学习模型可以如何合作。

首先，数学家必须将前沿理论转化为计算机可读形式。近年来，包括陶哲轩在内的多位数学家呼吁用开源推理语言Lean表达数学成果(这也是AlphaProof模型答题的形式)。目前，这个生态系统已包含超过15万项定理，为未来基于深度学习的数学研究奠定了基础。这个工作不止需要数学界把已经发表的论文和证明转化成机器可读/可验证模式，它还可能改变数学家的工作流程。假如确信某些相对繁琐的需要列举不同情况证明步骤可以用人工智能证明，数学家会更多选择“大力出奇迹”的证明方式。曾经，有一万种分类的证明方法是不会被数学家尝试/接受的，因为审稿者也无法确认其正确性，但现在可以由人工智能完成。此外，众多数学家指出，在形式化证明助手Lean中，“简单命题”和“繁琐命题”的概念与人类直觉存在显著差异。随着Lean逐渐发展成为一种普遍应用的工具，人类数学家将担当起“向导”的关键职能，其核心任务是将数学问题的研究路径转化为Lean更易理解和处理的形式。

其次，存量数据和创造人工数据的方法将变得至关重要。2018年，DeepMind在预测蛋白质结构方面取得了超越人类的突破，这得益于全球生物实验室积累的大量蛋白质折叠数据。然而，真实世界的科研数据往往稀缺。高质量数据集，尤其是具有创新性的数据集，数量有限且难以获取。合成数据可以弥补这一缺口。精心设计的合成数据生成算法可以创造出包含各种抽象模式和推理路径的数据，帮助它训练出的深度学习模型培养更深层次的数学直觉和创造力。这个过程和AlphaProof/AlphaGeo研发一样，需要有对领域理解极深的人类做准备工作，并在模型能力和可扩展性上找到平衡点。由于深度学习中的规模法则目前尚未遇到瓶颈，我们有理由相信，合成无限量的训练和测试样本可以进一步提升深度学习模型的抽象能力，提高扩展性，甚至催生出更具创新性的思辨能力。

AlphaProof/AlphaGeo的突破是算力增大过程中产生“涌现能力”的有力证据。DeepMind在训练模型时使用了惊人的三百亿PetaFLOPS算力，相当于训练了GPT-4级别的大语言模型。近期，大语言模型的应用似乎进入了瓶颈期，市场上出现了认为“算力缺口”并不存在的观点，认为现有算力已足以支持大语言模型的市场需求。然而，DeepMind在IMO上的成果有力地反驳了这种观点——即使通用大语言模型的算力需求进入瓶颈，同等规模的算力仍然可以在科研前沿等高价值领域做出大量超越人类巅峰的工作。更重要的是，我们尚不清楚更高数量级的算力是否能在理论物理、能源和材料科学等更多人类智力巅峰领域取得超越人类的成果。另外，假如更高数量级的算力可以在深度学习领域有和人类一样的创新能力，那未来最好的科研模型可能完成自我迭代，指数式地超越人类智能极限。

人工智能超越人类智能的征程，或许才刚刚开始。

（作者系加拿大国际数学奥林匹克竞赛集训队员，普特南竞赛全球百强选手。2014年毕业于哈佛大学应用数学系，现致力于人工智能在金融领域实践。联系方式：nirvanatear@hotmail.com。）