如何优化 Go 语言的排序算法以实现最快速度？

发表时间: 2022-04-28 14:38

前言

说到排序算法，很多同学会想起快速排序、堆排序、冒泡排序这些耳熟能详的算法。了解得深一些的同学，也可能看过例如 Python 的 timsort 以及 C++ intro sort 之类的排序算法。

但是我们也会有很多疑问，例如 Go 语言中使用的快速排序和我们书上学到的快速排序有什么区别呢？如果我们自己写一个快排，会比 Go 语言自带的快吗？排序算法方面业界最新的进展是什么呢，有没有一个算法是最快的？

本篇文章会向大家介绍字节跳动-语言团队在 Go 语言排序算法的实践，我们使用了 pdqsort 算法 + Go1.18 泛型，实现了一个比标准库 API 在几乎所有情况下快 2x ~ 60x 的算法库。

此项改动已经被社区采纳合并进入 Go runtime 当中，成为默认的 unstable 排序算法，预计将会在 Go 1.19 中和大家见面，其中非泛型版本位于标准库 sort，泛型版本位于 exp/slices。

Proposal: https://github.com/golang/go/issues/50154
临时项目地址：https://github.com/zhangyunhao116/pdqsort

简介

Go、Rust、C ++ 的默认 unstable 排序算法虽然名义上叫快速排序（quicksort），但其实质是混合排序算法（hybrid sorting algorithm），它们虽然在大部分情况下会使用快速排序算法，但是也会在不同情况下切换到其他排序算法。

unstable 排序算法意味着在排序过程中，值相等的元素可能会被互相交换位置。

一般来说，常见的混合排序算法，都会在元素较少（这个值一般是 16 ~ 32）的序列中切换成插入排序（insertion sort），尽管插入排序的时间复杂度为 O(n^2)，但是其在元素较少时性能基本超越其他排序算法，所以在混合排序算法的方案中被经常使用。

在其他情况下，默认使用快速排序算法。然而，快速排序算法有可能因为 pivot 选择的问题（有些序列 pivot 选择不好，导致性能下降很快）而导致在某些情况下可能到达最坏的时间复杂度 O(n^2)，为了保证快速排序算法部分在最坏情况下，我们的时间复杂度仍然为 O(n* logn)。大部分混合排序算法都会在某种情况下转而使用堆排序，因为堆排序在最坏情况下的时间复杂度仍然可以保持 O(n* logn)。

一言以蔽之，目前流行的 unstable 排序算法基本都是在不同的情况下，使用不同的方式排序从而达到最优解。而我们今天介绍的 pdqsort 也是这一思想的延伸。

前置知识

介绍一些常见的基本的排序算法以及它们的特性。

Quicksort (classic)

Average-case：O(n*logn) Bad-case：O(n^2)

经典的快速排序（quicksort）主要采用了分治的思想，具体的过程是将一个 array 通过选定一个 pivot（锚点）分成不同的 sub-arrays，选定 pivot 后，使得这个 array 中位于 pivot 左边的元素都小于 pivot，位于 pivot 右边的元素都大于 pivot。由此，pivot 两边构成了两个 sub-arrays，然后对这些 sub-arrays 进行相同的操作（选定 pivot 然后切分）。当某个 sub-array 只有一个元素时，其本身有序，此时便可以退出循环。如此反复，最后得到整体的有序。

我们可以观察到，经典的 quicksort 主要过程就是两步：

choose pivot: 选择一个 pivot
partition: 使用 pivot 对 array 进行划分

总的来说，quicksort 的性能关键点在于选定 pivot，选择 pivot 的好坏直接决定了排序的速度，如果每次 pivot 都被选定为真正的 median（中位数），此时快排的效率是最高的。因此 pivot 的选择重点在于寻找 array 真正的 median，目前所有的 pivot 选择方案都是在寻找一个近似的 median。

为什么 pivot 选定为中位数使得快排效率最高？

详细解释可以参考：https://en.wikipedia.org/wiki/Quicksort#Formal_analysis。简单来说，pivot 如果选定为中位数，则大部分情况下每次 partition 都会形成两个长度基本相同的 sub-arrays，我们只需要 logn 次 partition 就可以使得 array 完全有序，此时时间复杂度为 O(n* logn)。在最坏情况下，我们需要 n-1 次 partition （每次将长度为 L 的 array 分为长度为 1 和 L - 1 的两个 sub-arrays）才能使得 array 有序，此时时间复杂度为 O(n^2)。

我们为何不直接寻找 array 真正的 median？

原因是因为 array 的长度太长的话，寻找真正的 median 是一个非常昂贵的操作（需要存储所有的 items），相比于寻找一个近似的 median 作为 pivot 会消耗更多的资源，如果找到正确 median 的消耗比使用一个近似 median 高的话，这就是一个负优化。折中的方案就是使用一个高性能的近似 median 选择方案。

基本所有针对 quicksort 的改进方案，都是通过改造这两步得到的，例如第一步可以使用多种不同的 pivot 选择方案（见附录），第二步则有诸如 BlockQuickSort 这样通过减少分支预测来提升性能的方案。

Insertion sort

插入排序的主要想法是，每一次将一个待排序的元素插入到前方已经排序好的序列中，直到插入所有元素。尽管其平均时间复杂度高达 O(n^2)，但是在 array 长度较短（这个值一般是 16 ~ 32）的情况下，在实际应用中拥有良好的性能表现。

Heap sort

堆排序是利用堆结构设计出来的一种排序算法。这个算法有一个非常重要的特性，其在最坏情况下的时间复杂度仍然为 O(n* logn)。故而很多混合排序算法利用了这一特性，将堆排序作为 fall back 的排序算法，使得混合排序算法在最坏情况下的理论时间复杂度仍然为 O(n* logn)。

pdqsort (pattern-defeating quicksort)

论文地址：https://arxiv.org/pdf/2106.05123.pdf

pdqsort (pattern-defating quicksort) 是 Rust、C++ Boost 中默认的 unstable 排序算法，其实质为一种混合排序算法，会在不同情况下切换到不同的排序机制，是 C++ 标准库算法 introsort 的一种改进。可以认为是 unstable 混合排序算法的较新成果。

其理想情况下的时间复杂度为 O(n)，最坏情况下的时间复杂度为 O(n* logn)，不需要额外的空间。

pdqsort 的主要改进在于，其对 common cases （常见的情况）做了特殊优化。因此在这些情况下性能超越了之前算法，并且相比 introsort 在随机序列的排序性能基本保持了一致。例如当序列本身有序、完全逆序、基本有序这些情况下都超越了大部分算法。其主要的思想是，不断判定目前的序列情况，然后使用不同的方式和路径达到最优解。

这里的算法细节描述的是
https://github.com/zhangyunhao116/pdqsort 中的实践，其大致相当于论文中的 PDQ 算法（没有来自 BlockQuickSort 的优化），并且加入了一些参数调整以及借鉴了部分其他 pdqsort 的实践优化。

注意，不同 pdqsort 实践中会有一些细微差异（因为语言以及接口的关系），不过其总体思想是一致的。

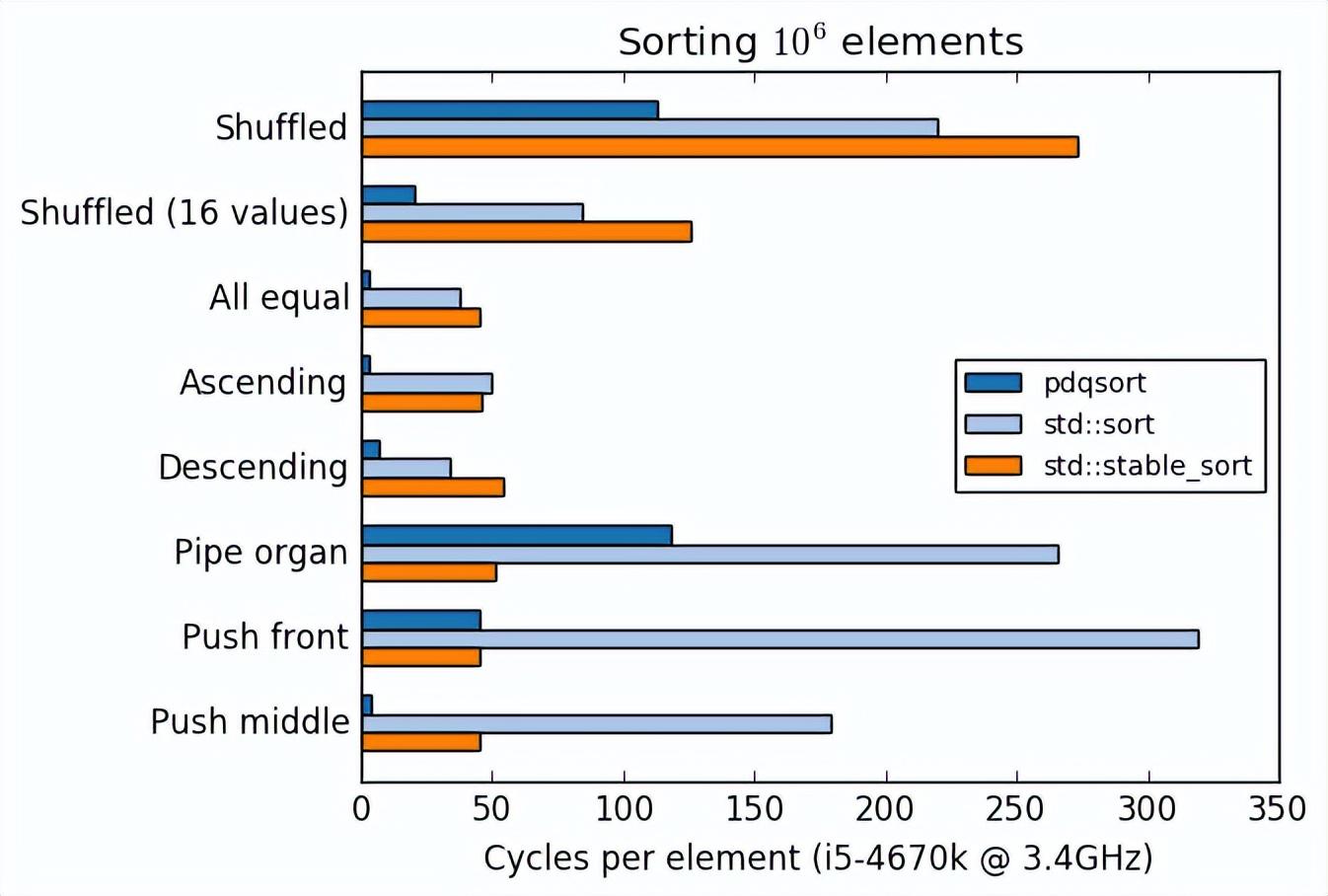
pdqsort C++ 版本性能对比，位于
https://github.com/orlp/pdqsort

整体流程

为了更好地解析 pdqsort 算法，我们先来描述下其主要流程。pdqsort 就是下面三种情况的不断循环，根据序列长度以及是否是最坏情况，每个 array 都会使用下面三种方法之一进行排序（有优先级，尽可能使用排在前面的方式）

短序列情况，对于长度在 [0, MAX_INSERTION] 的输入，使用 insertion sort （插入排序）来进行排序后直接返回，这里的 MAX_INSERTION 我们在 Go 语言下的性能测试，选定为 24。
最坏情况，如果发现改进的 quicksort 效果不佳（limit == 0），则后续排序都使用 heap sort 来保证最坏情况时间复杂度为 O(n*logn)。
正常情况，对于其他输入，使用改进的 quicksort 来排序，这里的算法分几步，后续内容会详细介绍部分步骤。

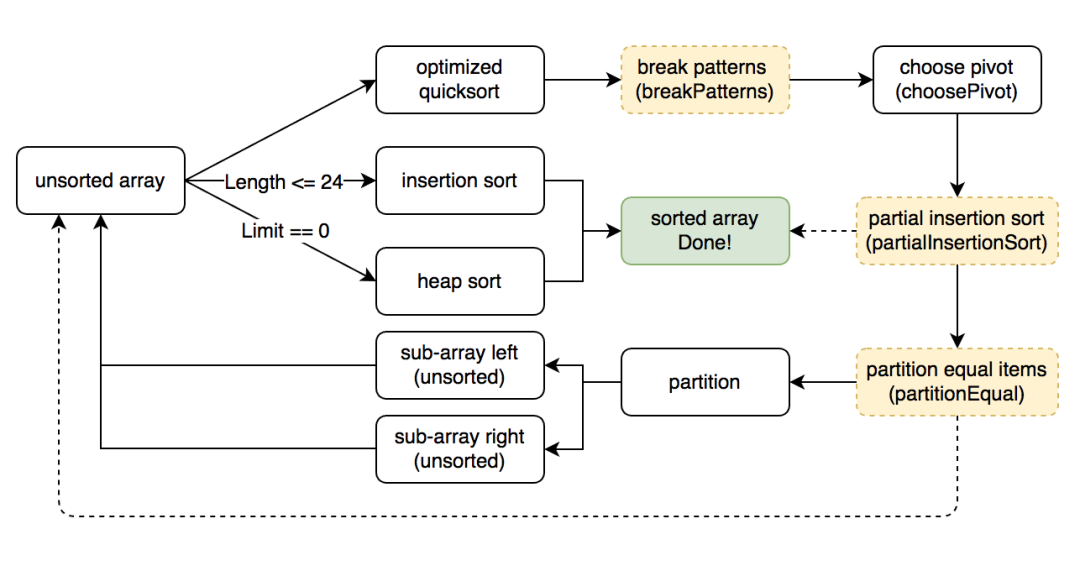
图中浅黄色虚线框代表此步骤为可选项，即算法会根据情况（以下变量）来决定是否执行。

下列变量代表 pdqsort 进行本次循环排序的情况，用于帮助算法来猜测需要排序的 array 的状态，来决定某些步骤是否需要进行

wasBalanced: Bool, 代表上次 partition 是否平衡。在 pivot 和真正的 median 很接近时我们认为是平衡的（true），此变量可以用 partition 后的 pivot index 同 array 两端的距离来判定。
wasPartitioned: Bool, 如果为真，则代表上次 partition 没有交换任何元素（即上次 partition 分割的是一个本身已经有序的 array）。
limit: int，如果为 0，则后续对 unsorted array 的排序都会使用 heap sort 而不是 quick sort。这种情况发生在 quicksort 有很多次选择的 pivot 和真正的 median 差距很大，从而导致 partition 后的两个 sub-arrays 长度相差较大的场景中。limit 的初始值是根据待排序 array 的长度计算出来的，每次发现快排策略效果不佳时，即 !wasBalanced 为真，则使得 limit 减小 1。

3-1. 应对可能的最坏情况，即实现中的breakPatterns。此时会判断 wasBalanced 是否为 true，如果不平衡（false），则随机交换几个元素，破坏一些可能造成 pivot 与 median 相差较大的特殊情况。

3-2. pivot 的选择，即实现中的 choosePivot。函数同时返回两个值，pivotidx 和 likelySorted，前者是 pivot 在此 array 的 index（索引），后者代表着选择 pivot 的过程中，是否可以大概率认定这个 array 已经为有序。

3-3. 应对几乎有序的情况，即实现中的 partialInsertionSort。如果 wasBalanced && wasPartitioned && likelySorted 为 true，则代表此 array 有非常大的可能是一个有序序列。此时我们使用 partial insertion sort 的排序算法，其原理和 insertion sort 大致相当，只是多了一个尝试次数，即只会对有限的元素进行插入排序，增加这个限制是为了避免猜测错误导致消耗大量时间。如果达到尝试次数时 array 仍未有序，则退出。如果在尝试次数之前发现所有元素有序，则可以直接返回。

3-4. 应对重复元素较多的情况，即实现中的 partitionEqual 。如果 pred 存在，并且和本次选中的 pivot 值相等（pred 是之前 array 的 pivot，即目前 array 中的最小值，因为与 pivot 重复的元素只可能出现在 partition 后的两个 sub-arrays 其中之一），说明重复元素很可能较多，则调用 partitionEqual 然后继续进行下次循环，使用这种方法将重复元素提前放到一起，因为多次选定重复元素作为 pivot 会使得 partition 的效率较低。

3-5. partition，使用 pivot 来分割 array，即实现中 partition。此函数和一般快排的 partition 相比基本相同，区别在于其会检测序列是否本身就是有序的（即 partition 时没有交换任何元素）。

实现细节

breakPatterns (3-1)

这一步的作用是解决一些会导致现有 pivot 选择方案表现很差的情况，所以当上次 partition 的 pivot 选择不好时（表现为最终 pivot 的位置离 array 两端之一很近），此时会随机交换几个元素来避免一些极端情况。同时，此步骤还会将 limit 减去 1，说明上次 pivot 的选取方案不够好（当 limit 为 0 时使用 heapsort 而不是快排方案来进行排序）。

pivot 选择 (3-2)

附录中有关于 pivot 选择方案的详细介绍。

假设 array 的长度为 L，
SHORTEST_MEDIAN_OF_MEDIANS 值为 50。这里根据长度分为三种情况：

L 位于 [0,8): 直接取固定值作为 pivot，即 L/4 * 2
L 位于 [8,SHORTEST_MEDIAN_OF_MEDIANS): 使用 medians of three 方法采样 3 个元素筛选 pivot，即 L/4* 1 L/4* 2 L/4* 3 的中间值
L 位于 [SHORTEST_MEDIAN_OF_MEDIANS, ∞): 使用 Tukey’s median of medians 采样 9 个元素得到一个近似中间值

此方法还会判断这个 array 是否很可能已经有序，例如当第三种情况时，如果发现 a a-1 a+1 这三个值中，a 恰好是中间值（b,c 也同样如此），则说明元素在这些地方都局部有序，所以这个 array 很可能是已经有序的。如果每次都发现，a a-1 a+1 这三个值都是逆序排列（b,c 也同样如此），则说明元素在这些地方都局部逆序，整个 array 很可能是完全逆序的。此时的策略是将整个 array 翻转，这样有很大概率使得整个 array 几乎有序。

Go 语言环境下的实践考量

Go 1.18 泛型对于排序算法的影响

Go 1.18 的泛型在这种情况下有较大的性能提升并且增加了可维护性，同样的算法在经过泛型改造后能得到 2x 的性能提升。这一点我们通过观察 pdqsort 泛型版本，以及 pdqsort (with sort.Interface) 的版本性能对比可以观察出来。

在可维护性方面，通过泛型的类型约束抽象了所有可比对的基本类型，不需要使用复杂的代码生成技术。

在性能方面，泛型由于有了类型参数，可以在编译期生成大量代码，免去了使用 sort.Interface 带来的抽象开销。

pdqsort 相比于 Go 原有算法的优势

在纯粹的算法层面，即 pdqsort (with sort.Interface) ，pdqsort 在完全随机的情况下和原有算法（类似于 IntroSort）性能几乎一致（非泛型版本，因为需要兼容 sort.Interface）。在常见的场景下（例如序列有序|几乎有序|逆序|几乎逆序|重复元素较多）等情况下，会比原有的算法快 1 ~ 30 倍。

因此，我们同样向 Go 官方提议将 pdqsort 应用在 sort.Sort 中，相关的 issue 讨论位于：https://github.com/golang/go/issues/50154

Go 原有的算法类似于 introsort，其通过递归次数来决定是否切换到 fall back 算法，而 pdqsort 使用了另一种计算方式（基于序列长度），使得切换到 fall back 算法的时机更加合理。

为什么禁用来自 BlockQuickSort 的优化

因为 BlockQuickSort 的优化基本来自减少分支预测，原理是在 partition 一个长序列的时候，先存储需要交换的元素，后续统一放到真正的序列中。经过实际性能测试，发现这一优化在 Go 上并不成立，甚至是一个负优化。原因可能由于 Go 是一门 heap-allocate 的语言，对于此类优化并不敏感。并且对于减少分支预测，Go 的编译器在某些情况下并不能优化到相应指令（CMOV）。

总结

目前大部分工业界使用的 unstable 排序算法，基本上都从过去教科书中单一的排序算法转变成混合排序算法，来应对实践场景中各式各样的序列。

pdqsort 依靠其在常见场景相比之前算法的性能优势，逐渐成为 unstable 排序算法的主流实现。基于 Go1.18 带来的泛型，使得排序算法的实现被大大简化，也给予了我们实现新算法的可能。但是 pdqsort 也不是万能灵药，在某些情况下，其他的算法依然保持着优势（例如 Python 标准库的 timsort 在混合升序&&降序的场景优于 pdqsort）。不过在大部分情况下，pdqsort 依靠其对于不同情况的特定优化，成为了 unstable 算法较好的选择。

附录

quicksort pivot 方案对比

这里简单介绍不同的 pivot 选择方案。最好的 pivot 选择方案就是使用一个高性能的近似 median 选择方案，在准确度和性能上达到平衡。假设我们需要排序的元素为 [4,3,2,1]，我们需要将其排列为升序，即 [1,2,3,4]。

选择首个元素

这是我们实现快排时最简单的方法，即选取 array 的首个元素作为 pivot。

[4,3,2,1]。选定 4 为 pivot，由于左边没有元素，所以会从最右边开始找，找到第一个比 4 小的元素，即 1 作交换。
[1,3,2,4]。选定 1 为 pivot，同理。希望从右边找到第一个比 1 小的元素，由于 1 已经是最小的值，此轮不会交换任何元素。
[1,3,2,4]。选定 3 为 pivot，同理。将 2 和 3 互换。
[1,2,3,4]。得到结果。

可以看到，选择首个元素的方式在 array 为逆序的情况下，每轮 partition 只将问题的规模减小了 1，即每次只能确定一个元素的最终位置。这种简单的方法在面对极端情况时效果并不好，在完全逆序的情况下达到了快排的最坏情况。

median of three

这个方法是分别取最左边、最右边、中间三个值，然后选出其中间值作为 pivot。例如 [4,3,2,1]，我们会选取 4 3 1 然后选择其中的 3 作为 pivot。这种方式相比于首个元素的方式会更加合理，因为采样了多个元素，不容易受到一些极端情况的影响，往往会比首个元素的方式有更好的效果。

stackoverflow discussion:
https://stackoverflow.com/questions/7559608/median-of-three-values-strategy

median of medians

这个方法的原理其实和 median of three 相似，不同的地方在于加大了 pivot 的采样范围，在 array 长度较长的情况下理论表现会更好。其采样步骤是先将 array 分为 n/5 个 sub-arrays，n 为 array 的长度。然后将这些 sub-arrays 的 medians 都取出，选取这些 medians 中的 median，同样的方式如此反复，最后得到一个 median of medians 作为最后的 pivot。

stackoverflow discussion:
https://stackoverflow.com/questions/5605916/quick-sort-median-selection
Median-finding Algorithm:
https://brilliant.org/wiki/median-finding-algorithm/#citation-1

John Tukey’s median of medians

此方法其实是 median of three 的改进，我们在 median of three 会取三个元素，而 Tukey’s median of medians 会取三个元素及其相邻两个元素的 median（例如 median of three 取了 a,b,c 则此方案会选择 a-1 a a+1 取这三个值的 median），然后再取这个三个 medians 的 median。即此方案会采样其中 9 个元素，相比于 median of three 多了三倍的采样率，所以此方法也叫做 Tukey’s ninther。

See
https://www.johndcook.com/blog/2009/06/23/tukey-median-ninther/