图是一种经典的数据结构，顺序表和链表都是线性结构结点之间的关系是一对一，二叉树及B树都是树形结构，结点之间是一对多的关系，而图是非线性结构，结点之间是多对多的关系。接下来讲一下图的存储，遍历和图的应用。

图的存储

线性表和树的存储主要使用顺序存储和链接存储两种方式。图的存储同样采用顺序方式和链接方式，但与之不同的是，图不光存储数据还要还要处理结点之间的关系。

1. 邻接矩阵

邻接矩阵(Adjacency Matrix ) 是表示顶点之间邻接关系的矩阵。在这种方法中，付图中的顶点采用顺序存储，因此需要一个顺序表来存储各个顶点，而用邻接矩阵来存储各条边。为了顺序存储图中的各个顶点，需要将顶点按任意的原则排成一个序列，每个顶点在北序列中都有一个序号，这个序号在存储边的邻接矩阵的中也会用到。

2. 邻接表

邻接表(AdiaeencyList) 是图的一种链接存储结构， 类似于树的孩子链表表示法。在这种方法中，顶点仍然是采用顺序方式进行存储，而用n个单链表来存储图中的边。其中第i个单链表是由所有与第i个顶点相关联的边链接而成的，称此单链表为第i个顶点的边表，边表中的每个结点称为边表结点。在存储顶点的顺序表中，每个结点增加一个指针域用来存放各个边表的头指针，称此顺序表为顶点表，而顺序表中的结点称为顶点表结点。顶点表和各顶点的边表一起组成图的邻接表。

3. 边集数组

图的边集数组法(EdgesetArray)是图的一种顺序存储方式，利用一维数组来存储图中所有的边。数组中的每个元素用来存储图中的一条边，包括始点、终点的序号及权值，该数组中所含元素的个数要大于等于图中边的条数。一般情况下，各条边在数组中的次序是任意的，但在实际问题中可根据具体情况而定。边集数组只是存储图中所有边的信息，如果需要存储顶点，同样需要一个具有n个元素的一维数组。

图的遍历

‬深度优先遍历

深度优先搜索(Depth - First Search) 遍历类似于树的先根遍历。对于给定的图G， 假设初始时所有顶点均未被访问过，则可从G中任选一顶点vi作为初始出发点。深度优先搜索可定义为：访问出发点v i，置访问标记为1，然后依次从vi的未被访问过的邻接点vj出发，继续进行深度优先搜索，直至图中所有与vi有路径相通的顶点均被访问过为止。很显然图的深度优先搜索过程是递归的，它的特点是尽可能先对图从纵深方向进行搜索，故称为深度优先搜索。

深度优先遍历

广度优先遍历

广度优先搜索( Breadth-First Search ) 遍历类似于树的层序遍历。对于给定的图G， 假一设初始时的所有顶点均未被访问过，可从图G中任选一顶点v.为初始出发点。广度优先搜索遍历可定义为：首先访问出发点vi，接着依次访问：的所有未被访问过的邻接点w1、w2，…，Wt，，然后，再依次访问与W1，W2，，W t，相邻接的未被访问过的顶点。依此类推，直至图中所有和初始出发点v；有路径相通的顶点都已访问到为止。显然，此方法的特点是尽可能先对图从横向进行搜索，故称之为广度优先搜索。为了实现广度优先搜索遍历算法，同样需要记录图中已被访问过的顶点，这里用一个辅助队列。

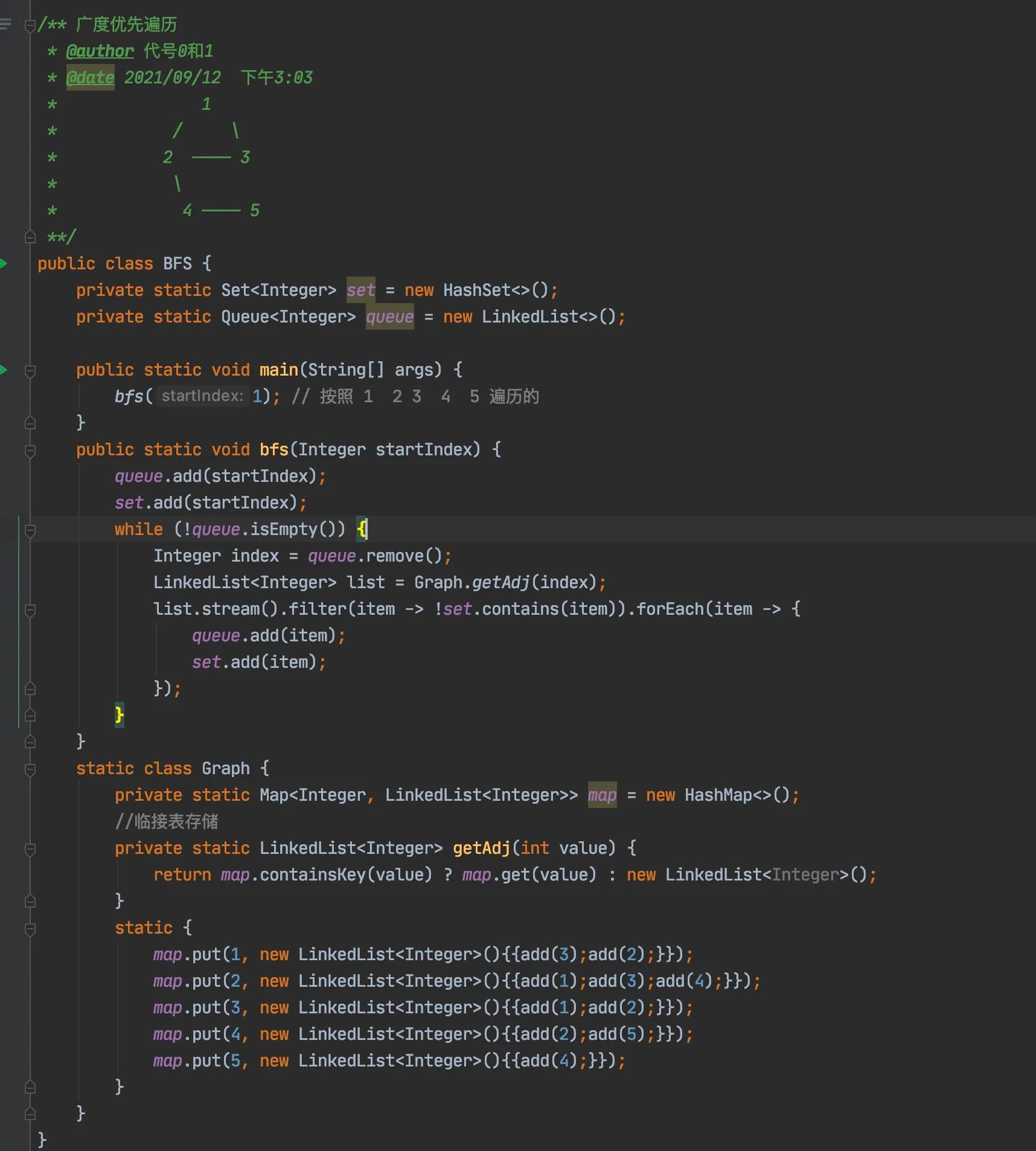
广度优先队列

最短路径

最短路径问题是图论中研究的一个经典问题，旨在寻找带权图中两顶点之间的最短路径。最短路径问题通常可以分成4种不同的情况：从图中某一顶点到达另一顶点的最短路径，即单源点、单目标点最短路径问题；从图中某一顶点到达各个顶点的最短路径，即单源点、多目标点最短路径问题；从图中任意顶点到达某个顶点的最短路径，即多源点、单目标点最短路径问题；从图中任意顶点到达其他任意顶点的最短路径，即多源点、多目标点最短路径问题。下面讨论最短路径问题中较常见的两种情况：单源点最短路径和任意两点间的最短路径。

单源最短路径Dijkstra

单源最短路径问题即单源点、多目标点的情况，需要求从图中某一顶点到达其余各个顶点的最短路径。对于给定的有向网络G=(V，E)和单个源点v，也就是求从源点v出发到G的其余各顶点的最短路径。

如何求得这些路径及长度呢?迪杰斯特拉(Dijksta) 经过研究提出了一个按照路长度递增的次序逐步产生最短路径的算法。算法的基本思想是：对于一个给定的存向网络G=(V，E)，设置一个逐步扩充的集合S，S中存放已经求出最短路径的顶点，那么尚未求出最短路径的顶点集合为V-S。很显然，算法的初始状态是集合S中只有源点，以后的每一步都是按照最短路径长度递增的顺序，逐个将V-S中已经找到最短路径的顶点加人到集合Ｓ中，用以扩充S。若从源点到V-S中某个顶点的路径不存在，此时可以认为从源点到该顶点有一条路径长度为无穷大的虚拟路径。在这样的假设条件下，不断扩充Ｓ直到S=V时，算法结束。

单源最短路径Dijkstra

任意两点间最短路径 多源最短路径

任意两点间最短路径问题即多源点、多目标点的情况。设给定的有向网络为G=E)，对G中任意的两个不同顶点的u和u，求出从顶点u到顶点u的最短路径。

在讨论了迪杰斯特拉算法之后，不难得出任意两点间最短路径问题的求法：依次向网络中的每个顶点作为源点，重复执行迪杰斯特拉算法n次，便可求出每一对顶点之最短路径。本小节要介绍另外一种解决此问题的算法， 这个算法是由弗洛伊德(Floy出来的， 称为弗洛伊德算法(Floyd算法) 。

弗洛伊德算法仍然是采用带权的邻接矩阵A来存储有向网络。其基本思想是：初时任意两点间的最短路径，即为两点之间边上的权值，然后依次在路径上加入各个顶2，3，…，n。每加人一个顶点，都要检查各条路径上经过此点后是否会使路径变短，这可保证在邻接矩阵中始终保存两点间的当前最短路径。

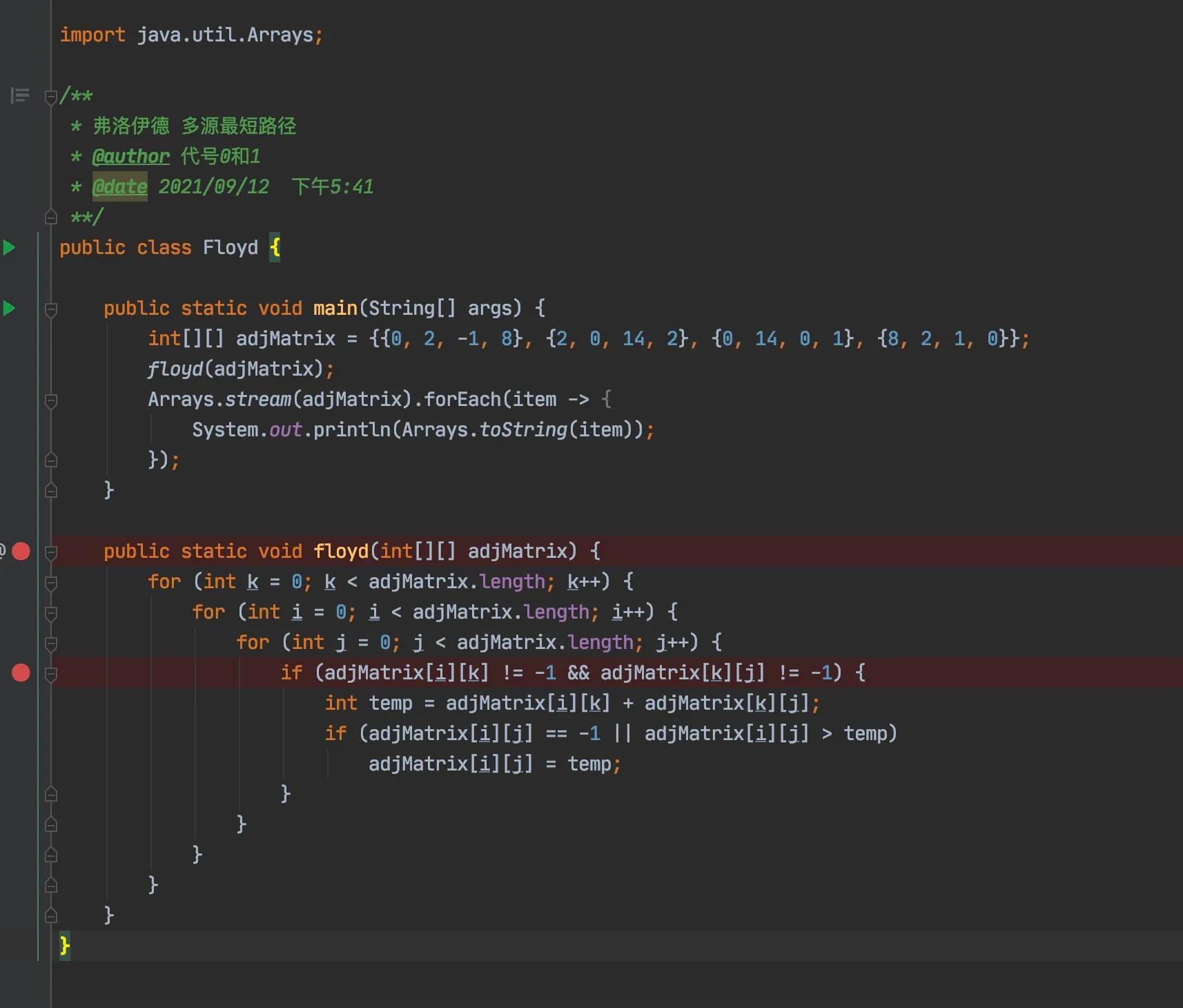
任意两点间的最短路径

‬图的其它应用

例如A*算法，最大网络流，拓扑排序，欧拉路径，哈密尔顿路径，二分图问题等，都使用了图的存储及遍历这些基础概念，一生二，二生三，三生万物，万物生于无形于有，不要被表象给迷糊住。人生到处知何似，应似飞鸿踏雪泥，留下印记再走呗……