图

图的定义

图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G（V,E），其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

线性表中我们把数据元素叫元素，树中将数据元素叫结点，在图中数据元素，我们则称之为顶点（Vertex）

图中，任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示

无向边：若顶点vi到vj之间的边没有方向，则称这条边为无向边（Edge），用无序偶对（vi,vj）来表示

有向边：若从顶点vi到vj的边有方向，则称这条边为有向边，也称为弧（Arc）

图的存储结构

邻接矩阵

用两个数组来表示图

一个一维数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息

邻接表

数组与链表相结合的存储方法

对边或弧使用链式存储的方式来避免空间浪费的问题。

十字链表

将邻接表和逆邻接表结合起来

除了结构复杂一点外，其实创建图算法的时间复杂度是和邻接表相同

图的遍历

从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次的过程

深度优先遍历DFS

它从图中某个顶点v出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到

若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

广度优先遍历BFS

相当于是层序遍历，先遍历小的，然后逐层扩大

最小生成树

把构造连通网的最小代价生成树

1. 普里姆算法
2. 克鲁斯卡尔算法

最短路径

指两顶点之间经过的边上权值之和最少的路径，并且我们称路径上的第一个顶点是源点，最后一个顶点是终点

1. 迪杰斯特拉算法
2. 弗洛伊德算法

拓扑排序

介绍

在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系，这样的有向图为顶点表示活动的网，我们称为AOV网

拓扑排序，其实就是对一个有向图构造拓扑序列的过程

拓扑排序算法

1. 每个顶点出现且只出现一次。
2. 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面
3. 有向无环

关键路径

AOE网：在一个表示工程的带权有向图中，用顶点表示事件，用有向边表示活动，用边上的权值表示活动的持续时间，这种有向图的边表示活动的网

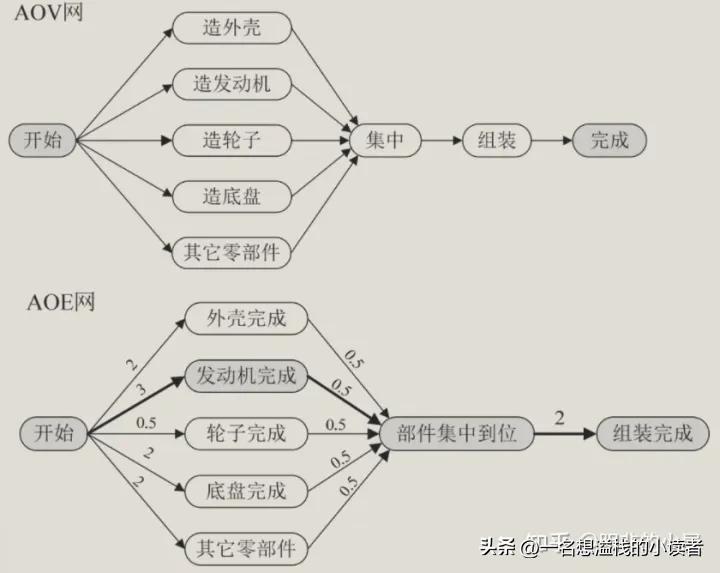
路径长度：路径上各个活动所持续的时间之和

关键路径：从源点到汇点具有最大长度的路径

关键活动：在关键路径上的活动