前言

数据结构是为实现对计算机数据有效使用的各种数据组织形式，服务于各类计算机操作。不同的数据结构具有各自对应的适用场景，旨在降低各种算法计算的时间与空间复杂度，达到最佳的任务执行效率。

如下图所示，常见的数据结构可分为「线性数据结构」与「非线性数据结构」，具体为：「数组」、「链表」、「栈」、「队列」、「树」、「图」、「散列表」、「堆」。

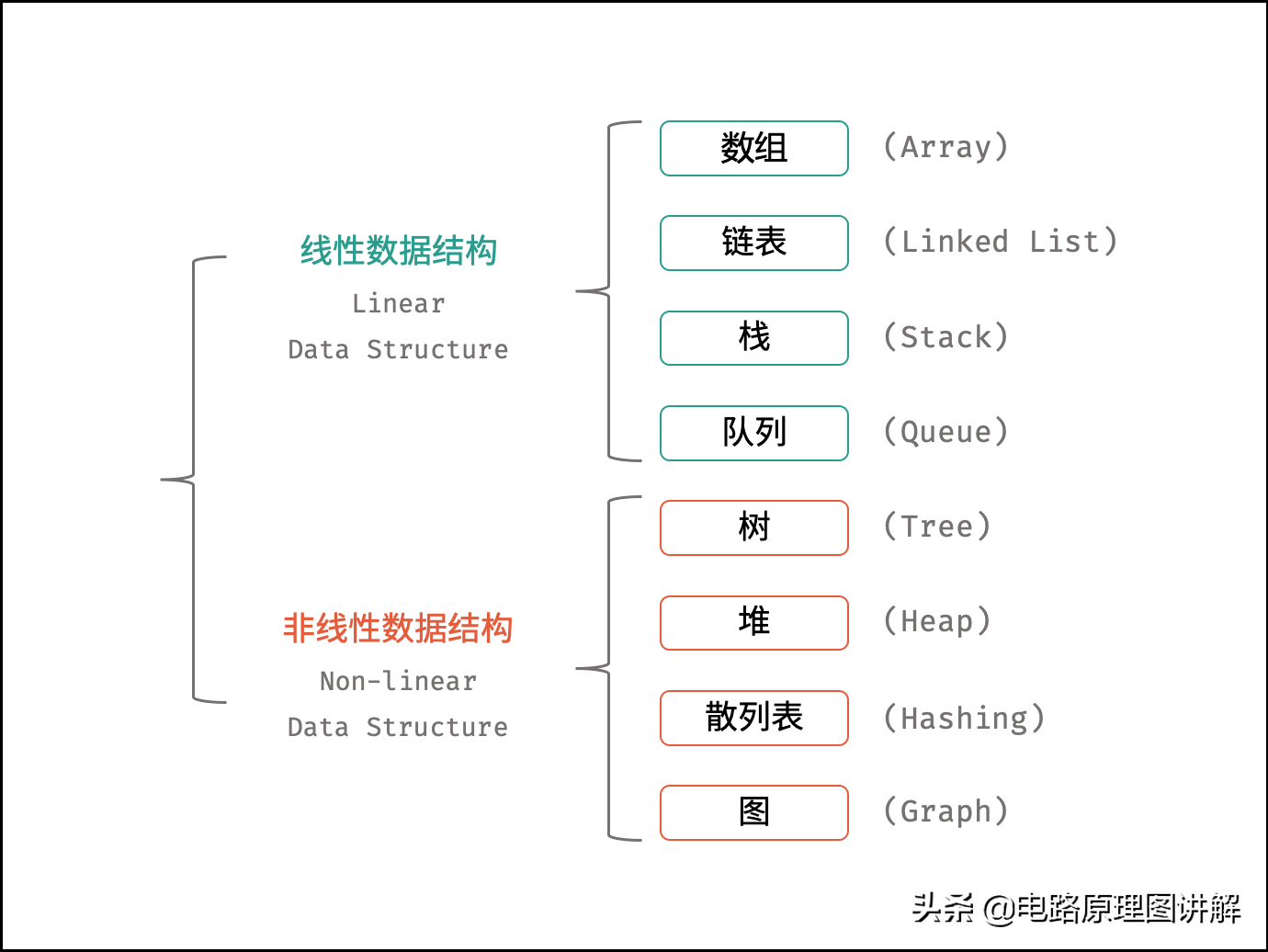
从零开始学习算法的同学对数据结构的使用方法可能尚不熟悉，本节将初步介绍各数据结构的基本特点，与 Python3 语言中数据结构的初始化与构建方法。

数组

数组是将相同类型的元素存储于连续内存空间的数据结构，其长度不可变。

「可变数组」是经常使用的数据结构，其基于数组和扩容机制实现，相比普通数组更加灵活。常用操作有：访问元素、添加元素、删除元素。

# 初始化可变数组array = []# 向尾部添加元素array.append(2)array.append(3)array.append(1)array.append(0)array.append(2)

链表

链表以节点为单位，每个元素都是一个独立对象，在内存空间的存储是非连续的。链表的节点对象具有两个成员变量：「值 val」，「后继节点引用 next」 。

class ListNode:    def __init__(self, x):        self.val = x     # 节点值        self.next = None # 后继节点引用

如下图所示，建立此链表需要实例化每个节点，并构建各节点的引用指向。

# 实例化节点n1 = ListNode(4) # 节点 headn2 = ListNode(5)n3 = ListNode(1)# 构建引用指向n1.next = n2n2.next = n3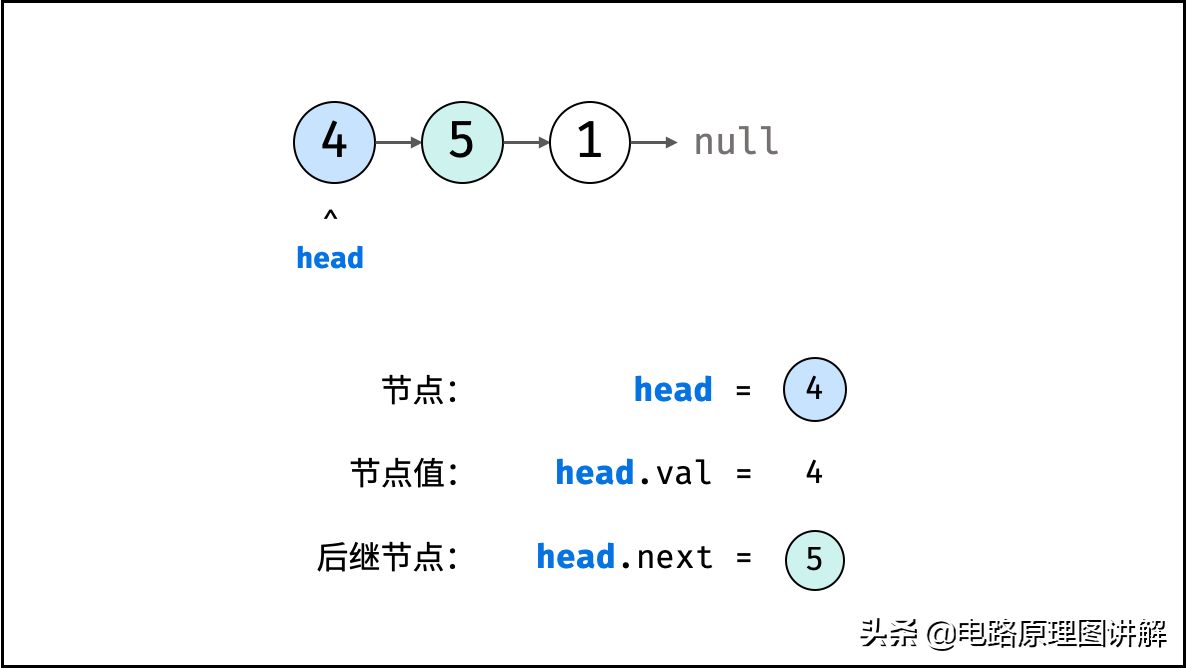

栈

栈是一种具有 「先入后出」 特点的抽象数据结构，可使用数组或链表实现。

stack = [] # Python 可将列表作为栈使用

如下图所示，通过常用操作「入栈 push()」,「出栈 pop()」，展示了栈的先入后出特性。

stack.append(1) # 元素 1 入栈stack.append(2) # 元素 2 入栈stack.pop()     # 出栈 -> 元素 2stack.pop()     # 出栈 -> 元素 1

注意：通常情况下，不推荐使用 Java 的 Vector 以及其子类 Stack ，而一般将 LinkedList 作为栈来使用。详细说明请见：Stack，ArrayDeque，LinkedList 的区别 。

// JavaLinkedList<Integer> stack = new LinkedList<>();stack.addLast(1);   // 元素 1 入栈stack.addLast(2);   // 元素 2 入栈stack.removeLast(); // 出栈 -> 元素 2stack.removeLast(); // 出栈 -> 元素 1

队列

队列是一种具有 「先入先出」 特点的抽象数据结构，可使用链表实现。

# Python 通常使用双端队列 collections.dequefrom collections import dequequeue = deque()

如下图所示，通过常用操作「入队 push()」,「出队 pop()」，展示了队列的先入先出特性。

queue.append(1) # 元素 1 入队queue.append(2) # 元素 2 入队queue.popleft() # 出队 -> 元素 1queue.popleft() # 出队 -> 元素 2

树

树是一种非线性数据结构，根据子节点数量可分为 「二叉树」 和 「多叉树」，最顶层的节点称为「根节点 root」。以二叉树为例，每个节点包含三个成员变量：「值 val」、「左子节点 left」、「右子节点 right」 。

class TreeNode:    def __init__(self, x):        self.val = x      # 节点值        self.left = None  # 左子节点        self.right = None # 右子节点

如下图所示，建立此二叉树需要实例化每个节点，并构建各节点的引用指向。

# 初始化节点n1 = TreeNode(3) # 根节点 rootn2 = TreeNode(4)n3 = TreeNode(5)n4 = TreeNode(1)n5 = TreeNode(2)# 构建引用指向n1.left = n2n1.right = n3n2.left = n4n2.right = n5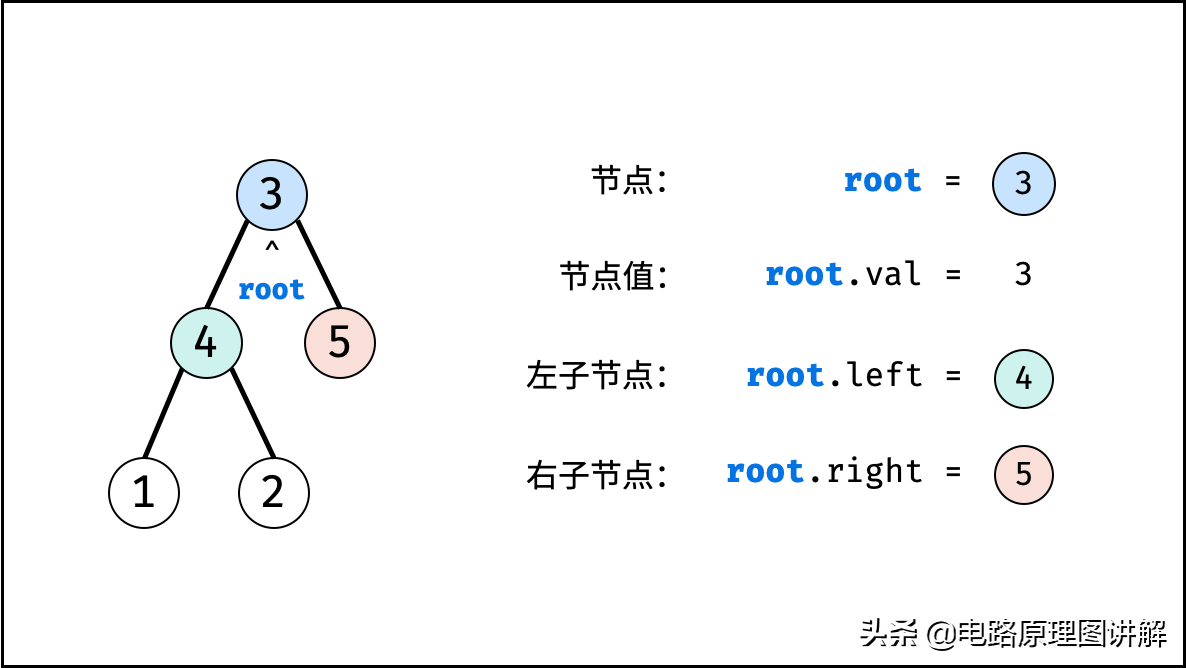

图

图是一种非线性数据结构，由「节点（顶点）vertex」和「边 edge」组成，每条边连接一对顶点。根据边的方向有无，图可分为「有向图」和「无向图」。本文 以无向图为例 开展介绍。

如下图所示，此无向图的 顶点 和 边 集合分别为：

• 顶点集合： vertices = {1, 2, 3, 4, 5}
• 边集合： edges = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 4), (3, 5), (4, 5)}

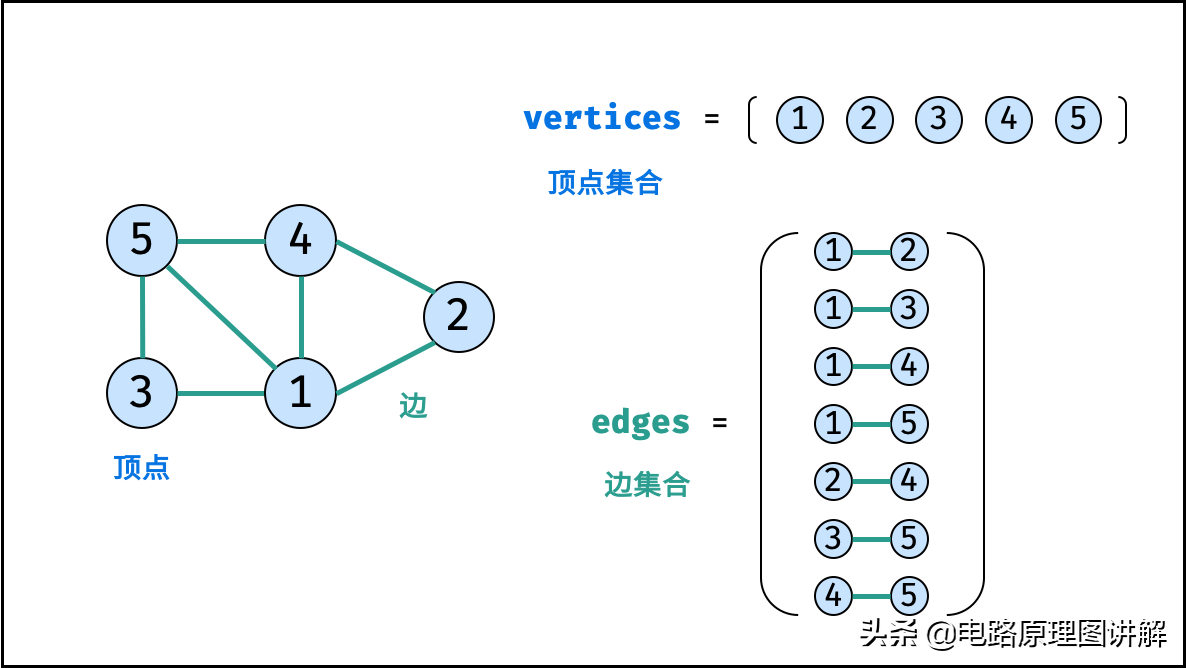
表示图的方法通常有两种：

1.邻接矩阵： 使用数组 vertices存储顶点，邻接矩阵 edges 存储边； edges[i][j] 代表节点 i + 1 和节点 j + 1之间是否有边。

邻接矩阵

vertices = [1, 2, 3, 4, 5]edges = [[0, 1, 1, 1, 1],         [1, 0, 0, 1, 0],         [1, 0, 0, 0, 1],         [1, 1, 0, 0, 1],         [1, 0, 1, 1, 0]]

2.邻接表： 使用数组 vertices 存储顶点，邻接表 edges 存储边。 edges 为一个二维容器，第一维 i代表顶点索引，第二维 edges[i] 存储此顶点对应的边集和；例如 edges[0] = [1, 2, 3, 4]代表 vertices[0] 的边集合为 [1, 2, 3, 4]。

vertices = [1, 2, 3, 4, 5]edges = [[1, 2, 3, 4],         [0, 3],         [0, 4],         [0, 1, 4],         [0, 2, 3]]

邻接矩阵 VS 邻接表 ：

邻接矩阵的大小只与节点数量有关，即 N^2 ，其中 N 为节点数量。因此，当边数量明显少于节点数量时，使用邻接矩阵存储图会造成较大的内存浪费。

因此，邻接表 适合存储稀疏图（顶点较多、边较少）； 邻接矩阵 适合存储稠密图（顶点较少、边较多）。

散列表

散列表是一种非线性数据结构，通过利用 Hash 函数将指定的「键 key」映射至对应的「值 value」，以实现高效的元素查找。

设想一个简单场景：小力、小特、小扣的学号分别为 10001, 10002, 10003 。

现需求从「姓名」查找「学号」。

则可通过建立姓名为 key ，学号为 value 的散列表实现此需求，代码如下：

JavaPythonC++

# 初始化散列表dic = {}# 添加 key -> value 键值对dic["小力"] = 10001dic["小特"] = 10002dic["小扣"] = 10003# 从姓名查找学号dic["小力"]   # -> 10001dic["小特"]   # -> 10002dic["小扣"]   # -> 10003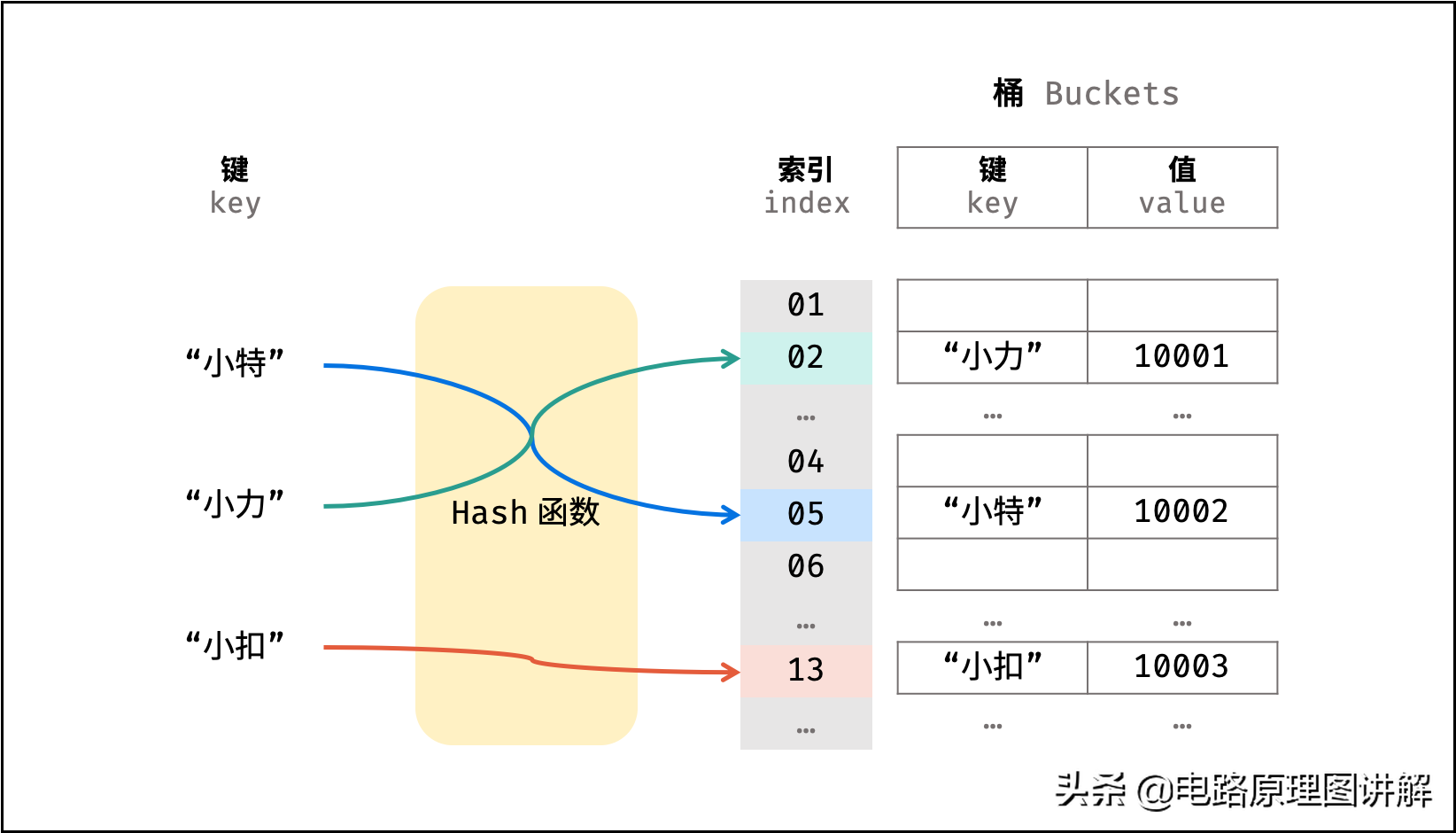

Hash 函数设计 Demo ：

假设需求：从「学号」查找「姓名」。

将三人的姓名存储至以下数组中，则各姓名在数组中的索引分别为 0, 1, 2 。

JavaPythonC++

names = [ "小力", "小特", "小扣" ]

此时，我们构造一个简单的 Hash 函数（ % 为取余符号 ），公式和封装函数如下所示：

def hash(id):       index = (id - 1) % 10000      return index

则我们构建了以学号为 key 、姓名对应的数组索引为 value 的散列表。利用此 Hash 函数，则可在 O(1)时间复杂度下通过学号查找到对应姓名，即：

names[hash(10001)] // 小力names[hash(10002)] // 小特names[hash(10003)] // 小扣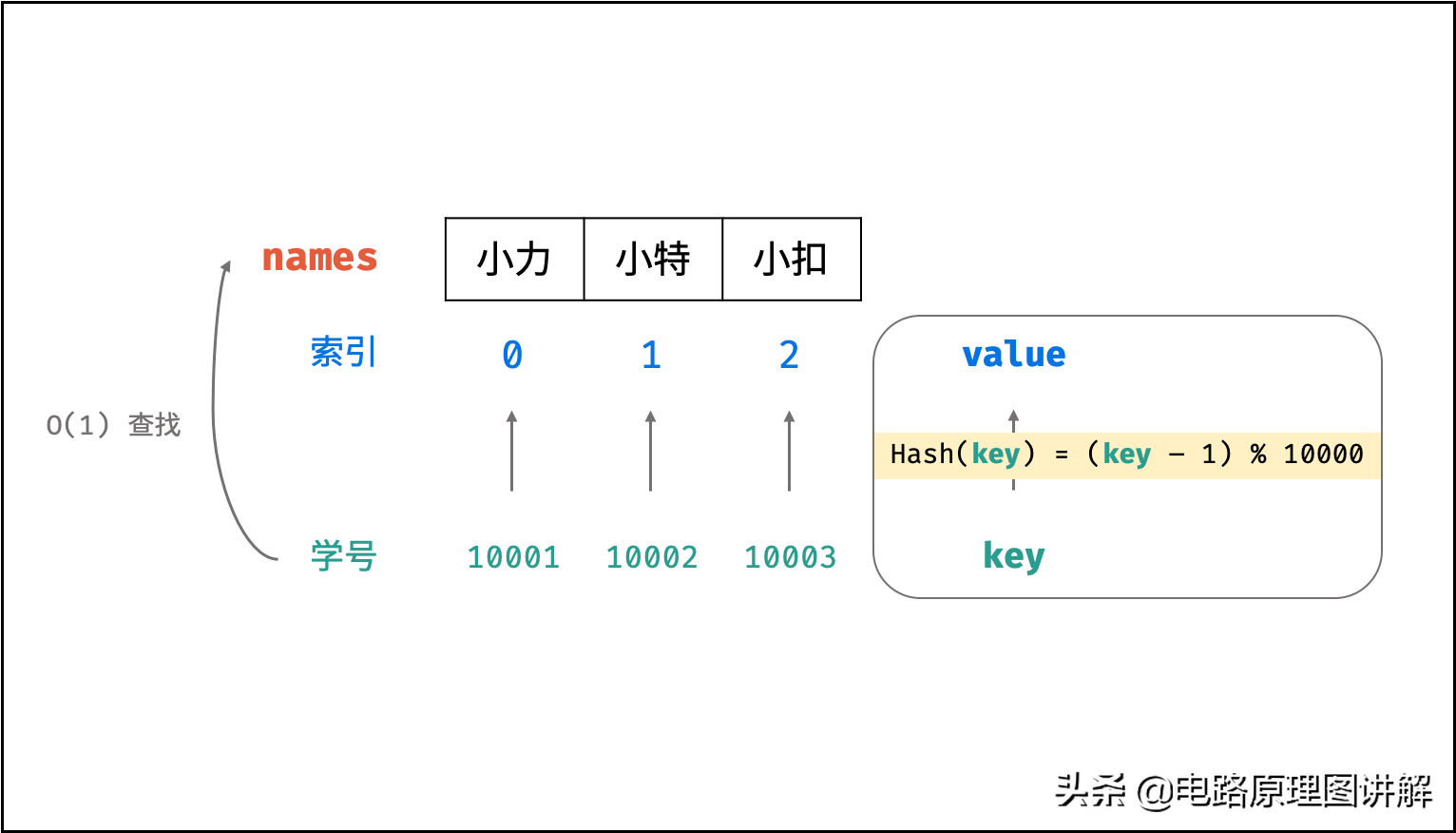

以上设计只适用于此示例，实际的 Hash 函数需保证低碰撞率、 高鲁棒性等，以适用于各类数据和场景。

堆：

堆是一种基于「完全二叉树」的数据结构，可使用数组实现。以堆为原理的排序算法称为「堆排序」，基于堆实现的数据结构为「优先队列」。堆分为「大顶堆」和「小顶堆」，大（小）顶堆：任意节点的值不大于（小于）其父节点的值。

完全二叉树定义： 设二叉树深度为 kk ，若二叉树除第 kk 层外的其它各层（第 11 至 k-1k−1 层）的节点达到最大个数，且处于第 kk 层的节点都连续集中在最左边，则称此二叉树为完全二叉树。

如下图所示，为包含 1, 4, 2, 6, 8 元素的小顶堆。将堆（完全二叉树）中的结点按层编号，即可映射到右边的数组存储形式。

通过使用「优先队列」的「压入 push()」和「弹出 pop()」操作，即可完成堆排序，实现代码如下：

from heapq import heappush, heappop# 初始化小顶堆heap = []# 元素入堆heappush(heap, 1)heappush(heap, 4)heappush(heap, 2)heappush(heap, 6)heappush(heap, 8)# 元素出堆（从小到大）heappop(heap) # -> 1heappop(heap) # -> 2heappop(heap) # -> 4heappop(heap) # -> 6heappop(heap) # -> 8

作者：Krahets

链接：
https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/50e446/

来源：力扣（LeetCode）

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。