栈概念

栈（stack）又名​堆栈​​​，它是一种​​运算受限​​​的​​线性表​​​。限定仅在​​表尾进行插入​​​和​​删除​​​操作的线性表。这一端被称为​​栈顶​​​，相对地，把另一端称为​​栈底​​​。向一个栈插入新元素又称作​​进栈、入栈或压栈​​​，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作​​出栈或退栈​​，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

稍微介绍一下关键名词：

运算受限：

也就是这个表你不能随便的删除插入。只能按照它的规则进行插入删除。比如栈就只能在一端插入和删除。同样，队列也是运算受限，只能在两端操作。

线性表：

栈也是一种线性表，前面详细介绍过线性表，它表达的是一种数据的逻辑关系。也就是在栈内各个元素是相邻的。当然在具体实现上也分​​数组和链表实现​​​，他们的物理存储结构不同。但是逻辑结构(​​实现的目的​​)相同。

栈顶栈底：

这个描述是偏向于逻辑上的内容，因为大家知道​​数组在末尾插入删除​​​更容易，而​​单链表通常在头插入删除​​更容易。所以数组可以用末尾做栈顶，而链表可以头做栈顶。

栈特点

同顺序表和链表一样，栈也是用来存储逻辑关系为 "一对一" 数据的线性存储结构

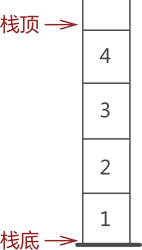
从上图我们看到，栈存储结构与之前所学的线性存储结构有所差异，这缘于栈对数据 "存" 和 "取" 的过程有特殊的要求：

1. 栈只能从表的一端存取数据，另一端是封闭的，如上图 所示；
2. 在栈中，无论是存数据还是取数据，都必须遵循"先进后出"的原则，即最先进栈的元素最后出栈。拿图 1 的栈来说，从图中数据的存储状态可判断出，元素 1 是最先进的栈。因此，当需要从栈中取出元素 1 时，根据"先进后出"的原则，需提前将元素 3 和元素 2 从栈中取出，然后才能成功取出元素 1。

栈的定义：限定只能在表的一端进行插入和删除运算的线性表（只能在栈顶操作）

逻辑结构：与同线性表相同，仍为一对一关系。

存储结构：用顺序栈（用顺序存储的话，就叫顺序栈）或链栈（用链式存储的话，就叫链栈）存储均可，但以顺序栈更常见

运算规则：只能在栈顶运算，且访问结点时依照后进先出（LIFO）的原则

实现方式：关键是编写入栈和出栈函数，具体实现依顺序栈和链栈的不同而不同栈与一般线性表的区别：仅在于运算规则不同。

栈的实现

一.数组模拟栈实现：

入栈过程

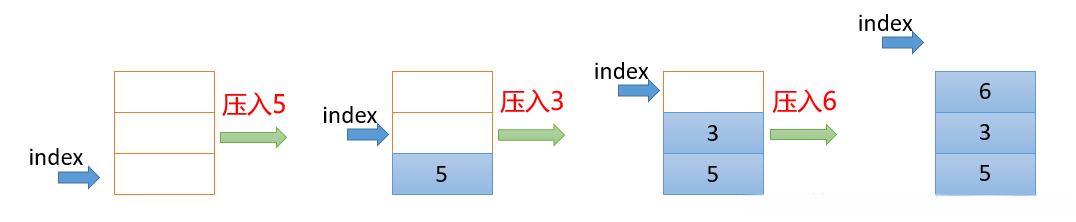
1.首先声明一个固定大小的数组arr，并将索引index指向0位置，压入数据的时候，先给arr[index]赋值，再将index++2.注意点：如果index=arr.length的时候，用户要入栈，给用户抛出“栈已满”的异常（上图最右边的情况）

弹栈过程

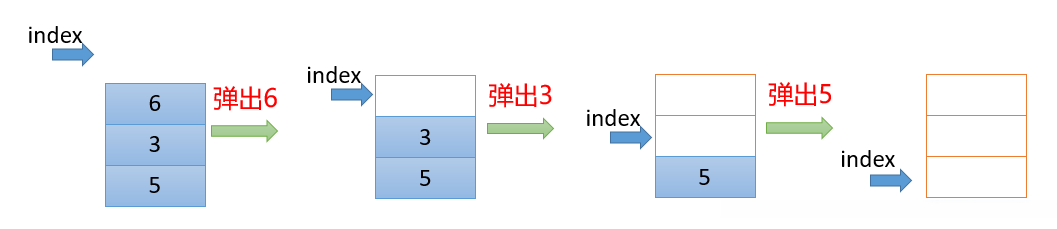
1.用户调用弹栈的功能的时候，先将index--,然后再将arr[index]返回即可2.注意点：如果index=0的时候，用户要弹栈，给用户抛出“栈为空”的异常（下图最右边的情况）3.如果用户只是要查看栈顶的数据，不是弹栈的话，只需要将arr[index-1]返回就行，但是不要添加index--功能（查看的时候，也需要先判断有没有数据，即index是否为0）

如果用户只是要查看栈顶的数据，不是弹栈的话，只需要将arr[index-1]返回就行，但是不要添加index--功能（查看的时候，也需要先判断有没有数据，即index是否为0）

代码实现

 public class ArrayStack {    //准备一个数组和一个指针    private Integer[] arr;    private Integer index;     //构造函数    public ArrayStack(int stackSize) {        if (stackSize < 0) {            throw new IllegalArgumentException("初始化大小不能小于0");        }        //初始化一个数组，并将指针指向索引0位置        arr = new Integer[stackSize];        index = 0;    }    //向栈中存入数据    public void push(int num){        if(index==arr.length){            throw new IllegalArgumentException("栈已满");        }        arr[index]=num;        index++;    }    //从栈中弹出数据    public Integer pop(){        if(index==0){            throw new  IllegalArgumentException("栈目前为空");        }        index--;        return arr[index];    }    //查看目前栈顶数据    public Integer peek(){        if(index==0){            return null;        }        return arr[index-1];    }}

二.链表模拟栈实现：

所谓链表（Linked list），就是按线性次序排列的一组数据节点，每个节点都是一个对象，它通过一个引用element指向对应的数据元素，同时还通过一个引用next指向下一节点。

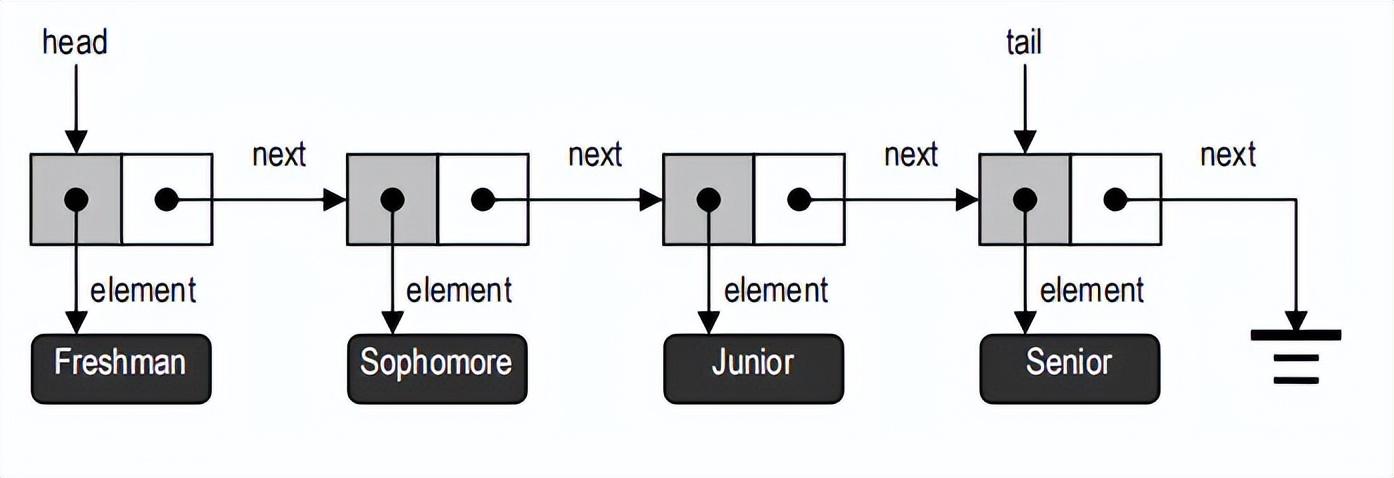
单链表结构

节点间这种相互指向的关系，乍看起来有循环引用之嫌，然而实际上却完全可行，而且不难实现。每个节点的next 引用都相当于一个链接或指针，指向另一节点。借助于这些 next 引用，我们可以从一个节点移动至其它节点。链表的第一个和最后一个节点，分别称作链表的首节点（Head）和末节点（Tail）。末节点的特征是，其next 引用为空。如此定义的链表，称作单链表（Singly linked list）。

Java实现单链表

package node;/** * @descrition * @since 2020-06-12 15:53 */public class Node {    private Object element;    private Node next;    public Node(Object element, Node next) {        this.element = element;        this.next = next;    }    public Object getElement() {        return element;    }    public void setElement(Object element) {        this.element = element;    }    public Node getNext() {        return next;    }    public void setNext(Node next) {        this.next = next;    }}

使用链表实现栈结构

定义空栈异常

package stack;/** * @descrition 空栈异常 * 对空栈使用top或pop方法时，此异常会被抛出 * @since 2020-06-10 14:31 */public class ExceptionStackEmpty extends RuntimeException {    public ExceptionStackEmpty(String message) {        super(message);    }}

定义栈接口

package stack;/** * @descrition 定义栈接口 * @since 2020-06-10 11:39 */public interface IStack {    // 返回栈中元素数目    int getSize();    // 判断栈是否为空    boolean isEmpty();    // 取栈顶元素（但不删除）    Object top() throws ExceptionStackEmpty;    // 入栈    void push(Object ele);    // 出栈    Object pop() throws ExceptionStackEmpty;}

定义栈实现

package node;import stack.ExceptionStackEmpty;import stack.IStack;/** * @description * @since 2020-06-12 16:23 */public class Stack_Node implements IStack {    // 指向栈顶元素    private Node top;    // 栈尺寸    private int size;    /**     * 空栈     */    public Stack_Node() {        this.top = null;        this.size = 0;    }    /**     * 获取栈尺寸     *     * @return     */    @Override    public int getSize() {        return this.size;    }    /**     * 判断栈是否为空     */    @Override    public boolean isEmpty() {        return size == 0;    }    /**     * 获取栈顶元素     */    @Override    public Object top() throws ExceptionStackEmpty {        if (isEmpty()) {            throw new ExceptionStackEmpty("空栈！");        }        Object result = top.getElement();        return result;    }    /**     * 压栈     */    @Override    public void push(Object obj) {        Node node = new Node(obj, top);        top = node;        size++;    }    /**     * 弹出栈顶     */    @Override    public Object pop() throws ExceptionStackEmpty {        if (isEmpty()) {            throw new ExceptionStackEmpty("空栈！");        }        Object result = top.getElement();        // 更新首节点引用        top = top.getNext();        // 更新栈尺寸        size--;        return result;    }}

对比于使用数组实现栈结构

相对于利用数组的实现，这一实现的另一优点在于，无需针对溢出问题而刻意去设置一个意外错。当然，溢出错误仍然会得到处理，只不过交由 JRE 来处理。这不仅统一和简化了错误的处理，而且更重要的是，出现栈溢出错误的可能性大大降低⎯⎯此时，只有在 JRE 没有剩余空间时才会出现栈溢出的现象；而在基于数组的实现中，只要超过数组的长度就会报栈溢出。这两种处理方法有着本质的区别，前者中 JRE 报告的OutOfMemoryError 属于错误（Error），而后者报告的ExceptionStackFull 属于意外（Exception）。

栈实现表达式求值

1、中、后缀表达式转换的原理

按中缀表达式转换成二叉树，再对二叉树进行后序遍历即可得到后缀表达式（中序遍历即为中缀表达式）。具体原理请参考百度相关资料，此处不再赘述

2、将中缀表达式转换为后缀表达式

a、思路：

初始化一个空字符串postfix，用来存放后缀表达式

初始化一个空栈opStack，用来对操作符进行出栈和入栈

遍历之前先判断括号匹配，若匹配则进行下一步，括号匹配也是栈的应用

遍历中缀表达式，取出字符判断：

1）若字符是数字（本例中仅进行了10以内的整数的简单四则运算），则加入到字符串 中

2）若字符是左括号（包括(、[、{），将其入栈

3）若字符是右括号（因为之前已判断过括号匹配，所以此时栈一定不为空）则判断 opStack栈顶字符，若栈顶字符是左括号，则退出循环，否则将栈顶的操作符加入字 符串postfix中

4）若字符是操作符，若栈opStack为空，将其入栈；否则，与栈顶字符比较两者的优先 级，若栈顶元素的优先级较低，则将当前字符入栈，否则将栈顶字符加入字符串po stfix中

5）若取出的字符既不是操作符也不是操作数，说明表达式出错，结束循环。

b、代码实现：

//转换成后缀表达式public boolean toPostfix(){    if( !isCorrect() ){        System.out.println("您的表达式输入有误，请检查后再输入");        return false;    }    Stack opStack = new Stack(infix.length());    //由于本题前导部分的限制原因，现仅考虑个位整数加减法    for(int i=0; i<infix.length(); i++){        char ch = infix.charAt(i);        if ( ch >='0' && ch <='9'){            //如果是操作数            postfix+=ch;        }else if(prority(ch)==0){            //如果是左括号,入栈            opStack.push(ch);        } else if (ch == ')' || ch == ']' || ch == '}') {            // 如果是右括号，因为前面已经判断过算式中括号匹配问题，所以此时遇到右括号，栈中必定有数据项            char chf = opStack.pop();            if (prority(chf) == 0) {            // 如果栈顶是左括号，则退出循环，说明算式中不再有其他运算符                break;            } else {        // 如果栈顶不是左括号则为普通操作符，说明括号中的运算符都已遍历完                postfix += chf;            }        } else if (prority(ch) > 0) {            // 如果是普通操作符            if (opStack.isNull()) {                // 如果栈不为空,入栈                opStack.push(ch);            } else {                char chf = opStack.peek();                int prof = prority(chf);                int pro = prority(ch);                if (prof == 0 || (prof > pro)) {                 // 如果栈顶是左括号或栈顶符号的优先级较低，则入栈                    opStack.push(ch);                } else if (prof <= pro && prof > 0) {                    // 如果栈顶操作符优先级更高,且不为左括号                    postfix += ch;                }            }        } else {// 既不是操作符也不是操作数，算式输入有误            System.out.println("您的表达式输入有误，请检查后再输入");            return false;        } // end of outer if-else    } // end of for    while (!opStack.isNull()) {        char ch = opStack.pop();        if (prority(ch) > 0) {            postfix+=ch;        } else            break;    }    return false;}

3、根据后缀表达式求值

a、思路

初始化一个空栈theStack，用来给操作数出入栈

遍历后缀表达式：

1）若字符是数字，则入栈theStack

2）若字符是操作数，因简单四则运算都是双目运算符，所以一次从栈中取出两个操作数，运 算后，将结果入栈

最后栈顶即是表达式的值

b、代码实现

public int calculate(){    int maxSize = postfix.length();    Stack theStack = new Stack(maxSize,1);    int op1;//操作数1    int op2;//操作数2    int tmp = 0;//中间结果    for(int index=0; index<maxSize; index++){        char ch = postfix.charAt(index);        if( ch >='0' && ch <='9' ){            //如果是操作数，则入栈            theStack.push(ch-'0');        }else{            //如果是操作符，则将操作数出栈，运算            op1 = theStack.pop(1);            op2 = theStack.pop(1);            switch(ch){            case '+':                tmp = op1+op2;                break;            case '-':                tmp = op2 - op1;                break;            case '*':                tmp = op2 * op1;                break;            case '/':                tmp = op2 / op1;                break;            }            theStack.push(tmp);        }//end of if-else    }//end of for    result = theStack.pop(1);    return result;}//end of calculate()

4、测试

测试代码：

public class InfixApp {    public static void main(String[] args) throws IOException {        // TODO Auto-generated method stub        System.out.println("please input an infix expression: ");        String input = getString();        Infix inf = new Infix(input);        inf.toPostfix();        System.out.println("the final postfix expression: "+inf.postfix);        inf.calculate();        System.out.println("the result is: "+inf.result);    }    public static String getString() throws IOException{        InputStreamReader isr = new InputStreamReader(System.in);        BufferedReader br = new BufferedReader(isr);        String str = br.readLine();        return str;    }}

栈的应用场景

• 1.子程序的调用：在跳往子程序前，会先将下一个指令的地址存到堆栈中直到子程序执行完毕后再将地址取出，以回到原来的程序中
• 2.处理递归调用：和子程序的调用类似，只是除了储存下一个指令的地址外也将参数，区域变量等数据存入堆栈中
• 3.表达式的转换【中缀表达式转后缀表达式】与求值（实际解决）
• 4.二叉树的遍历
• 5.图形的深度优化（depth-first）搜索法。