约瑟夫问题描述的是什么？

约瑟夫问题：有 N 个人围成一圈，每个人都有一个编号，编号由入圈的顺序决定，第一个入圈的人编号为 1，最后一个为 N，从第 k (1<=k<=N)个人开始报数，数到 m (1<=m<=N)的人将出圈，然后下一个人继续从 1 开始报数，直至所有人全部出圈，求依次出圈的编号。

如何存储数据

面对一道题，首先需要思考，要选用什么样的数据结构来保存数据。约瑟夫问题描述的是循环报数出圈的问题，报数始终围绕同一个方向进行，所以可以使用单向环形链表来存储。

每当有一个人入圈，就创建出一个新的节点，节点间首尾相连，代码如下：

//节点class Node {    //节点序号    private Integer no;    //指向下一个节点的引用    private Node next;    public Node(Integer no) {        this.no = no;    }    @Override    public String toString() {        return "Node{" +            "no=" + no +            ",next=" + (next == null ? "" : next.no) +            '}';    }}//单向环形链表class SingleCycleLinkedList {    //头引用    private Node head;    //尾引用    private Node tail;    //链表长度    private int size;    /**     * 初始化指定长度序号递增的环形链表     *     * @param size     */    public SingleCycleLinkedList(int size) {        for (int i = 1; i <= size; i++) {            add(new Node(i));        }        this.size = size;    }    /**     * 插入环形链表     *     * @param node     */    public void add(Node node) {        if (node == null) {            return;        }        //链表为空，直接将 head, tail 引用指向新节点        if (size == 0) {            head = node;            tail = node;            size++;            return;        }        //链表不为空，将新节点放在链表最后，同时新节点的 next 引用指向 head，完成成环操作        tail.next = node;        tail = tail.next;        tail.next = head;        size++;}    ...}

核心逻辑在 add 方法中，需要注意的是，当链表为空时，新增的节点不能自成环，也就是 next 引用不能指向自己，所以第一次新增时，直接将 head, tail 指向新增的节点，不去操作节点的 next 引用。当链表不为空时，需要引入成环的步骤，成环步骤分解如下：

1.tail.next = node

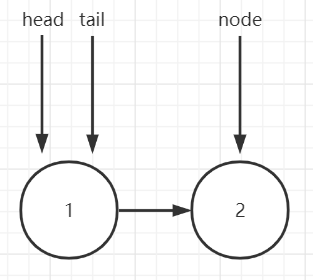
2.tail = tail.next

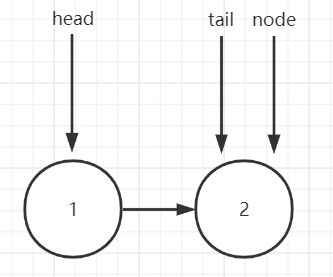
3.tail.next = head

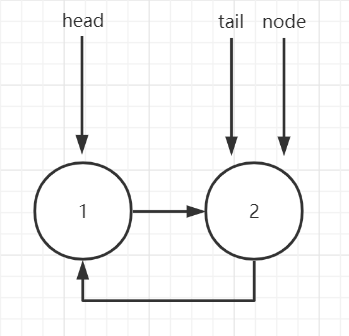
这样即完成了成环操作。

在 main 方法中进行测试，构造长度为 10 的环形链表：

SingleCycleLinkedList singleCycleLinkedList = new SingleCycleLinkedList(10);System.out.println(singleCycleLinkedList);

结果如下：

Node{no=1,next=2}, Node{no=2,next=3}, Node{no=3,next=4}, Node{no=4,next=5}, Node{no=5,next=6}, Node{no=6,next=7}, Node{no=7,next=8}, Node{no=8,next=9}, Node{no=9,next=10}, Node{no=10,next=1}

解决约瑟夫问题

通过上一步，完成了数据的存储，接下来需要解决如何循环报数出圈的问题。题目要求从第 k 个人开始报数，所以要先找到报数的起始位置，然后开始循环报数，数到 m 的人出圈，也就是对应的节点要移出链表。需要注意的是，单向链表的节点无法自我删除，如图所示：

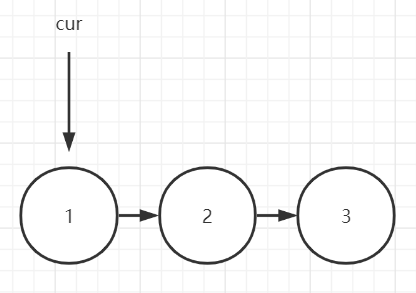
如果想删除编号为 2 的节点，cur 引用必须指向 1，这样才能将 1 的 next 引用从原来的 2 指向 3：

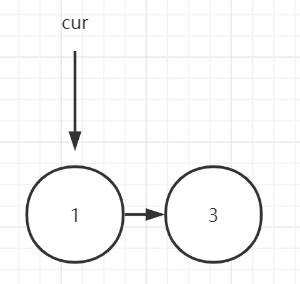
所以，在找报数的起始位置时，应当从起始位置的上一个位置开始计数，这样当寻找到待移除节点时，实际上是定位到了待移除节点的上一个节点。寻找报数起始位置的代码如下（代码中 start 变量就是参数 k）：

//寻找开始报数的节点(这里从 tail 开始遍历，取报数节点的上一个节点，因为单向链表的节点删除必须依赖上一个节点)Node tmp = tail;int startIndex = 0;while (startIndex++ != size) {  if (start == startIndex) {    break;  }  tmp = tmp.next;}

找到了报数起始位置后，就要开始执行报数的操作，移除节点时需要注意，当链表中的节点数量只剩一个时，无需操作节点的 next 引用，直接将节点置空即可。 报数出圈的代码如下（代码中 step 变量就是参数 m）：

//保存顺序出链的节点List<Node> list = new ArrayList<>(size);//开始计数，数到指定间隔后节点出链int count = 1;while (size > 1) {    if (count == step) {        //节点出链        //1.定义一个引用，指向待删除节点        Node delNode = tmp.next;        //2.将当前节点的 next 引用指向待删除节点的下一个节点        tmp.next = delNode.next;        //3.链表长度-1        size--;        //4.置空待删除节点的 next 引用        delNode.next = null;        //5.保存已删除节点        list.add(delNode);        //6.重置计数器        count = 1;    } else {        //继续循环计数        tmp = tmp.next;        count++;    }}//链表只剩一个节点时，不需要操作next指针删除节点，直接将头尾置空tmp.next = null;head = null;tail = null;size = 0;list.add(tmp);

注意，在移除节点后，必须要保证链表仍然成环，移除步骤分解如下（假设链表剩 3 个节点，要移出编号为 3 的节点）：

1.Node delNode = tmp.next

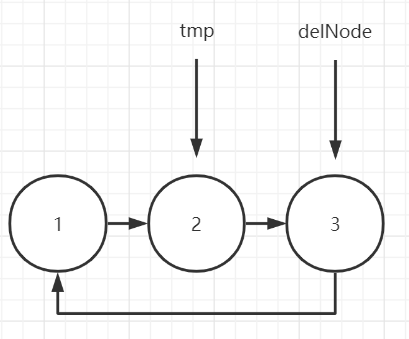
2.tmp.next = delNode.next

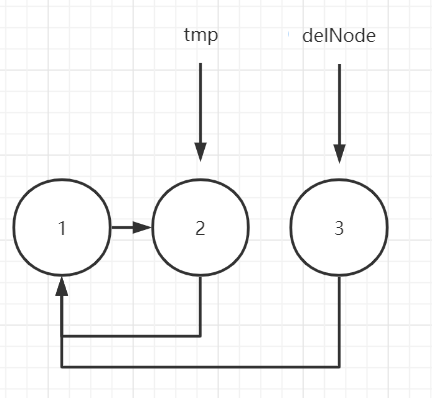
3.delNode.next = null

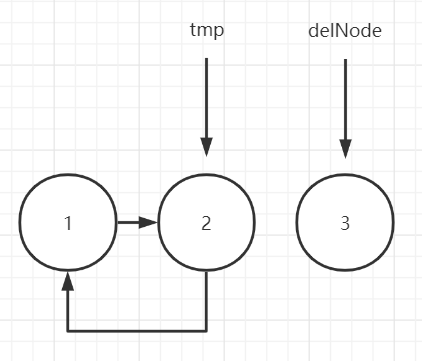
报数出圈的完整代码如下：

    /**     * 从 start 位置开始，每隔 step 后节点出链     *     * @param start 报数起始位置     * @param step 报数出圈间隔     * @return 依次出链的节点列表     */    public List<Node> poll(int start, int step) {        if (start <= 0 || start > size) {            throw new RuntimeException("起始位置需大于0并且小于等于链表长度");        }        if (step <= 0) {            throw new RuntimeException("间隔需大于0");        }        //寻找开始报数的节点(这里从 tail 开始遍历，取报数节点的上一个节点，因为单向链表的节点删除必须依赖上一个节点)        Node tmp = tail;        int startIndex = 0;        while (startIndex++ != size) {            if (start == startIndex) {                break;            }            tmp = tmp.next;        }        //保存顺序出链的节点        List<Node> list = new ArrayList<>(size);        //开始计数，数到指定间隔后节点出链        int count = 1;        while (size > 1) {            if (count == step) {                //节点出链                //1.定义一个引用，指向待删除节点                Node delNode = tmp.next;                //2.将当前节点的 next 引用指向待删除节点的下一个节点                tmp.next = delNode.next;                //3.链表长度-1                size--;                //4.置空待删除节点的 next 引用                delNode.next = null;                //5.保存已删除节点                list.add(delNode);                //6.重置计数器                count = 1;            } else {                //继续循环计数                tmp = tmp.next;                count++;            }        }        //链表只剩一个节点时，不需要操作next指针删除节点，直接将头尾置空        tmp.next = null;        head = null;        tail = null;        size = 0;        list.add(tmp);        return list;    }

对上述代码进行测试：

//n: 圈内人数, k: 报数的起始位置, m: 报数出队的间隔int n = 10;int k = 2;int m = 3;List<Node> pollList = singleCycleLinkedList.poll(k, m);System.out.printf("size: %d, start: %d, step: %d\n", n, k, m);System.out.println(pollList.stream().map(node -> node.no).collect(Collectors.toList()));

结果如下：

size: 10, start: 2, step: 3[4, 7, 10, 3, 8, 2, 9, 6, 1, 5]

数据验证

当 n = 10, k = 2, m = 3 时，节点移除的分解步骤如下：

完整节点：Node{no=1}, Node{no=2}, Node{no=3}, Node{no=4}, Node{no=5}, Node{no=6}, Node{no=7}, Node{no=8}, Node{no=9}, Node{no=10}

4 出圈：Node{no=1}, Node{no=2}, Node{no=3}, Node{no=5}, Node{no=6}, Node{no=7}, Node{no=8}, Node{no=9}, Node{no=10}

7 出圈：Node{no=1}, Node{no=2}, Node{no=3}, Node{no=5}, Node{no=6}, Node{no=8}, Node{no=9}, Node{no=10}

10 出圈：Node{no=1}, Node{no=2}, Node{no=3}, Node{no=5}, Node{no=6}, Node{no=8}, Node{no=9}

3 出圈：Node{no=1}, Node{no=2}, Node{no=5}, Node{no=6}, Node{no=8}, Node{no=9}

8 出圈：Node{no=1}, Node{no=2}, Node{no=5}, Node{no=6}, Node{no=9}

2 出圈：Node{no=1}, Node{no=5}, Node{no=6}, Node{no=9}

9 出圈：Node{no=1}, Node{no=5}, Node{no=6}

6 出圈：Node{no=1}, Node{no=5}

1 出圈：Node{no=5}

5 出圈

出圈顺序依次为： [4, 7, 10, 3, 8, 2, 9, 6, 1, 5]。与结果一致。