算法与数据结构：轻松掌握基础概念

算法和数据结构

一、算法及数据结构理解

算法是在有限的空间和时间下，使用具体的数学逻辑和特定的数据结构解决特定的问题。

数据结构是算法逻辑计算过程中的一种载体或形式。数据结构是进行数据存取、实现具体数学逻辑的具体方式。

在物理、生物、化学上有一句著名的话——结构决定功能。同样在数据结构的世界中，有什么样的数据结构就决定了能完成什么样的功能，决定了能否高效地完成某种操作。

假如有一种业务场景是：查找最后（最近）一次被插入的元素。那么你必须知道最后一个元素在所在的数据结构中的具体位置，才可以找到该元素。

如果你采用栈这种数据结构进行存取，栈具有天生的“先入后出”的操作逻辑，栈会给你一种先验知识，告诉你：栈顶的元素就是最后一个被插入的元素，那么你只需要返回栈顶的元素即可，即一次查找操作即可完成。同样的场景下，使用队列进行数据存取，你需要从队列头遍历到队列尾部才可以找到最后一个要查找的元素，即进行了多次查找和判断是否达到队列尾部，相对于栈，队列显然使用更多的比较次数。此场景下，栈这种数据结构的优势显而易见。

如上所述，相同的业务场景采用不同的数据结构会有明显的插入和取出的操作差异，针对具体问题，我们使用了特定的数据结构，就可以高效地解决它。

二、两种基本操作

在计算机使用场景中有两种最常用操作：排序和查找。不管你用Java、C、Python等各种语言实现，

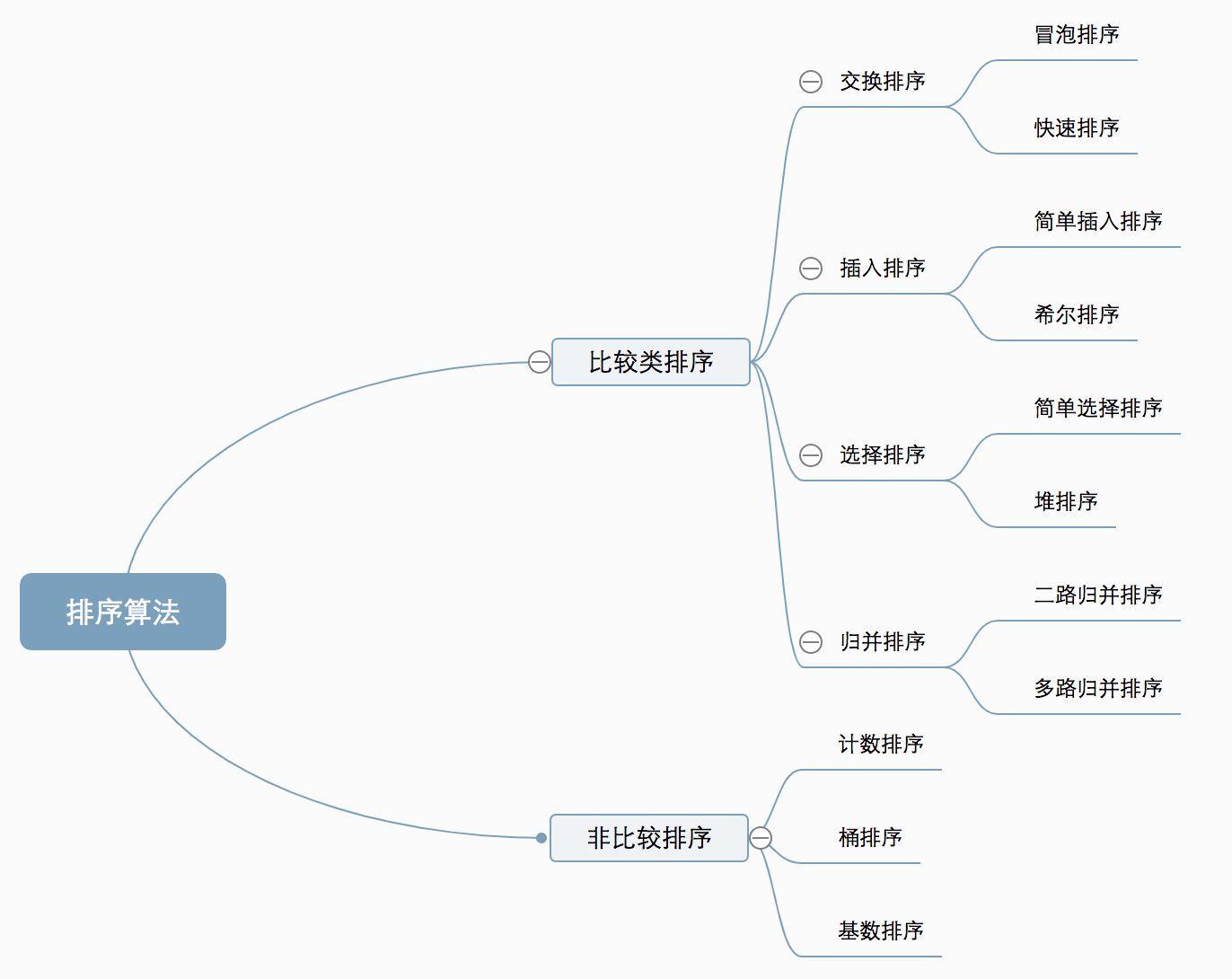
排序就是将给定的元素按照特定顺序进行排列。

排序算法

查找就是在特定的数据结构中找到要查找的元素。比如：

• 顺序查找（基于无序链表，效率低下）
• 有序数组中的二分查找
• 二叉查找树
• 红黑树
• 散列表

三、数据结构的抽象（API）

如果按照Java中一切都是对象的观点来看数据结构。我们可以把数据结构抽象为一种接口，接口只提供未实现的方法，即逻辑想法，如插入、删除、查找、数据结构元素个数等这些方法名，不含具体实现。具体实现由接口的具体实现的数据结构来完成，实现接口方法。

举个例子，在查找操作中，符号表这种数据结构是关联键和值的一种数据结构，通过键查找值的一种操作。符号表可当做一种抽象的接口，提供未实现的插入，查找等方法。它的具体实现的数据结构有哪些呢？典型的有二叉查找树、平衡查找树、散列表。

符号表的API:

//Java语言public class SymbolicTable extends Comparable<Key, Value> {	SymbolicTable()	void put(Key key, Value val)	Value get(Key key)	boolean contains(Key key)	boolean isEmpty()	int size()	key min()	Key max() }

一种类型的散列表实现：

//基于拉链的散列表public class SeparateChainingHashST<Key, Value> {    private int M;    private int N;    private SeparateChainingHashST<Key, Value>[] st;    public SeparateChainingHashST(){    	this(997);    }    public SeparateChainingHashST(int M){    	this.M = M;    	st = (SeparateChainingHashST<Key, Value>[])new SeparateChainingHashST[M];        for(int i = 0; i < M; i++)        	st[i] = new SeparateChainingHashST();    }    public int hash(Key key){     	//Key的hashCode()若未覆盖Object的hashCode(),则key.hashCode()为Object的版本，取对象地址    	return (key.hashCode()& 0x7fffffff)%M;    }    public Value get(Key key){    	 return (Value)st[hash(key)].get(key);    }    public void put(Key key, Value val){    	st[hash(key)].put(key,val);    }}

四、数据结构底层数据结构

一般所说的数据结构是某种特定的具体的数据结构。数据结构底层一般是基于节点链表或者数组。

二叉查找树底层使用节点连接成的链表实现，散列表底层使用数组和节点链表实现。

五、算法性能

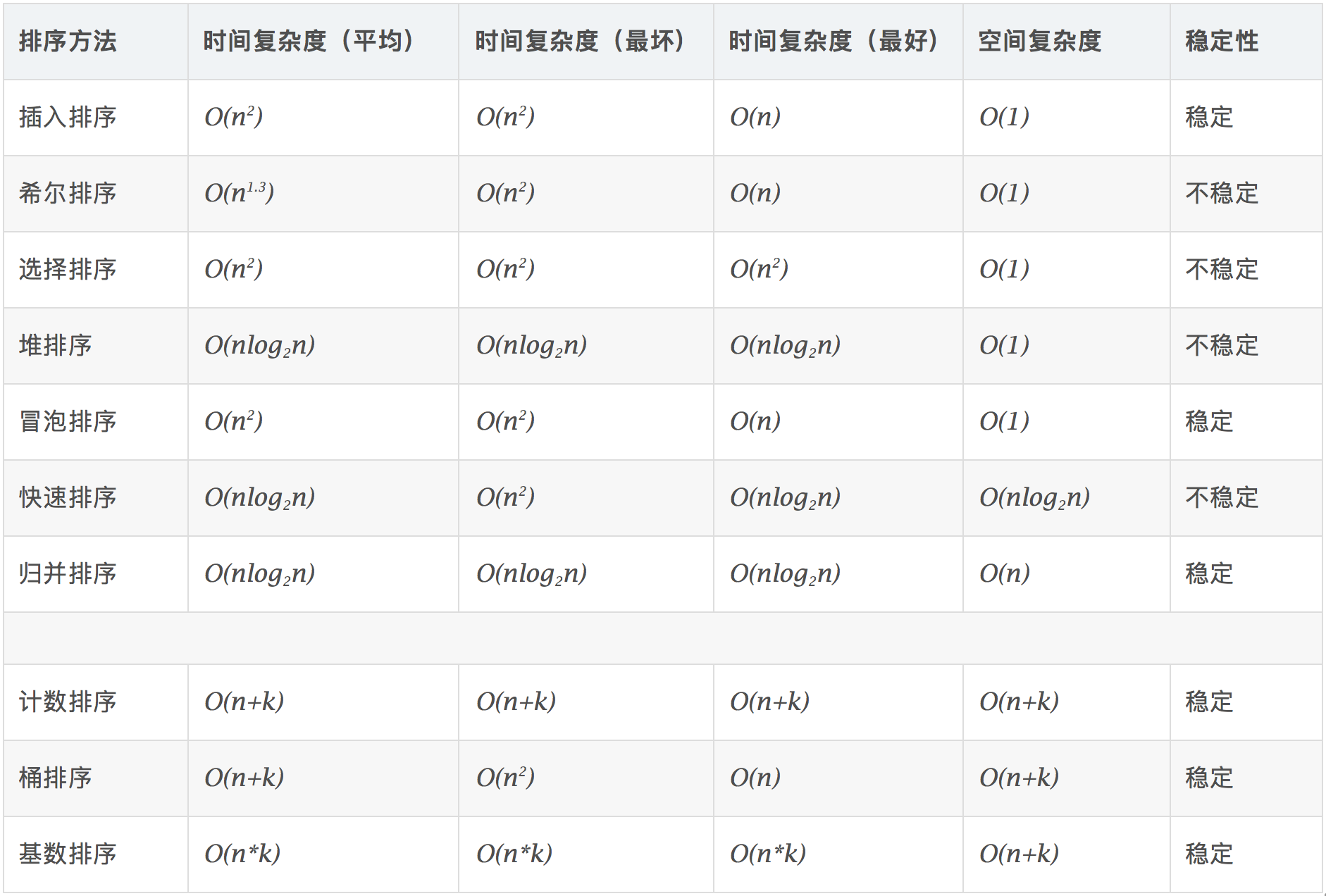
算法的性能一般使用时间复杂度和空间复杂度衡量。因为计算机硬件资源，如内存是有限的，同时完成一项任务又有时间要求，所以必须用时间和空间来衡量评估算法的性能，以合理的时间和空间完成特定任务。

复杂度