# 数据结构与算法（三）查找算法

## 目录

五、常见查找算法

1. 查找算法分类

2. 平均查找长度

3. 顺序查找

4. 二分法查找

5. 插值查找

6. 斐波那契查找

7. 分块查找

8. 哈希查找

9. 树查找

## 一、数学基础

## 二、算法分析

## 三、常见数据结构

## 四、常见排序算法

## 五、常见查找算法

### 查找算法分类

- 1. 静态查找和动态查找

- 注：静态或者动态都是针对查找表而言的。动态表指查找表中有删除和插入操作的表。

- 2. 无序查找和有序查找

- 无序查找：被查找数列有序无序均可；

- 有序查找：被查找数列必须为有序数列。

### 平均查找长度（Average Search Length，ASL）

- 需和指定key进行比较的关键字的个数的期望值，称为查找算法在查找成功时的平均查找长度。

对于含有n个数据元素的查找表，查找成功的平均查找长度为：ASL = Pi*Ci的和。

Pi：查找表中第i个数据元素的概率。

Ci：找到第i个数据元素时已经比较过的次数。

### 1. 顺序查找

- 1. 顺序查找适合于存储结构为顺序存储或链接存储的线性表

- 2. 基本思想

- 顺序查找也称为线形查找，属于无序查找算法。从数据结构线形表的一端开始，顺序扫描，依次将扫描到的结点关键字与给定值k相比较，若相等则表示查找成功；若扫描结束仍没有找到关键字等于k的结点，表示查找失败。

- 3. 算法分析

- 查找成功时的平均查找长度为：（假设每个数据元素的概率相等） ASL = 1/n(1+2+3+…+n) = (n+1)/2 ;

当查找不成功时，需要n+1次比较，时间复杂度为O(n);

所以，顺序查找的时间复杂度为O(n)。

- 4. 代码实现

### 2. 二分法查找

- 二分查找算法又叫作折半查找，要求待查找的序列有序，每次查找都取中间位置的值与待查关键字进行比较，如果中间位置的值比待查关键字大，则在序列的左半部分继续执行该查找过程，如果中间位置的值比待查关键字小，则在序列的右半部分继续执行该查找过程，直到查找到关键字为止，否则在序列中没有待查关键字。

- 1. 算法描述

- 二分查找算法要求要查找的集合是有序的，如果不是有序的集合，则先要通过排序算法排序后再进行查找。

- 2. 流程【图】

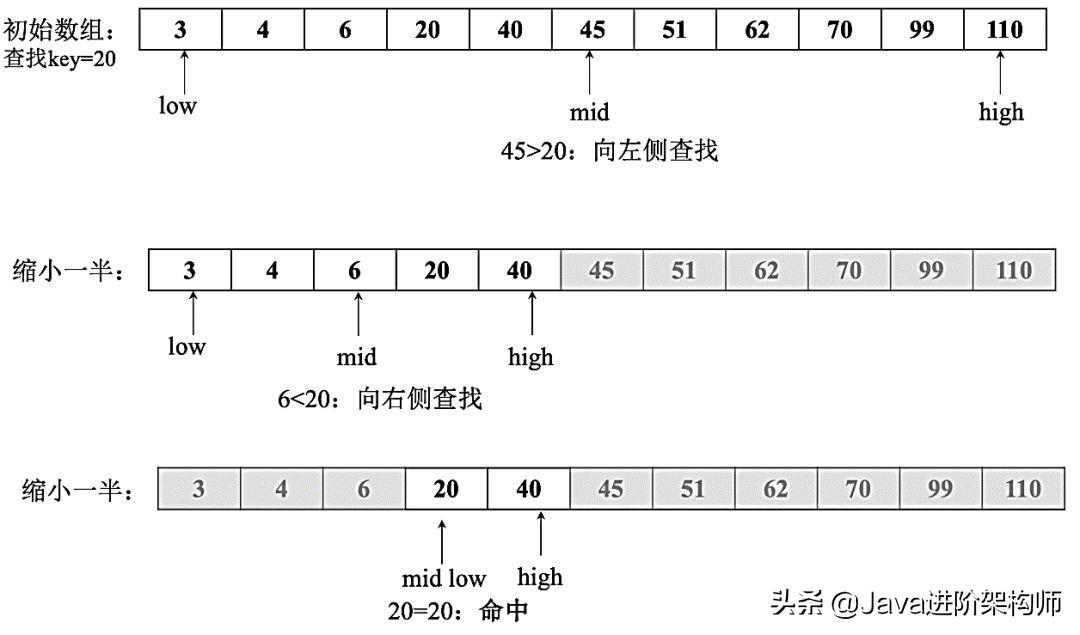
- 3. 代码实现

- 1. 定义3个变量low、mid和high，分别表示二分查找的最小、中间和最大的数据索引

- 2. 通过一个while循环在数组中查找传入的数据，在该数据大于中间位置的数据时向右查找，即最大索引位置不变，将最小索引设置为上次循环的中间索引加1

- 3. 在该数据小于中间位置的数据时向左查找，即最小索引位置不变，然后将最大索引设置为上次循环的中间索引并减1

- 4. 重复以上过程，直到中间索引位置的数据等于要查找的数据，说明找到了要查找的数据，将该数据对应的索引返回。

- 5. 如果遍历到low>high还没有找到要查找的数据，则说明该数据在列表中不存在，返回-1。

- 4. 算法分析

- ***最坏情况下，关键词比较次数为log2(n+1)，且期望时间复杂度为O(log2n)；

- 5. 使用场景分析

- 折半查找的前提条件是需要有序表顺序存储，对于静态查找表，一次排序后不再变化，折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说，维护有序的排序会带来不小的工作量，那就不建议使用

### 3. 插值查找

- 1. 算法描述

- 基于二分查找算法，将查找点的选择改进为自适应选择，可以提高查找效率。当然，差值查找也属于有序查找。

- 2. 复杂度分析

- 查找成功或者失败的时间复杂度均为O(log2(log2n))。

- 3. 代码实现

- mid=low+(key-a[low])/(a[high]-a[low])*(high-low)；

- 4. 使用场景分析

- 对于表长较大，而关键字分布又比较均匀的查找表来说，插值查找算法的平均性能比折半查找要好的多。反之，数组中如果分布非常不均匀，那么插值查找未必是很合适的选择。

### 4. 斐波那契查找

- 1. 简介

- 在介绍斐波那契查找算法之前，我们先介绍一下很它紧密相连并且大家都熟知的一个概念——黄金分割。

黄金比例又称黄金分割，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值约为1:0.618或1.618:1。

0.618被公认为最具有审美意义的比例数字，这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域，而且在管理、工程设计等方面也有着不可忽视的作用。因此被称为黄金分割。

大家记不记得斐波那契数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….（从第三个数开始，后边每一个数都是前两个数的和）。然后我们会发现，随着斐波那契数列的递增，前后两个数的比值会越来越接近0.618，利用这个特性，我们就可以将黄金比例运用到查找技术中。

- 2. 基本思想

- 也是二分查找的一种提升算法，通过运用黄金比例的概念在数列中选择查找点进行查找，提高查找效率。同样地，斐波那契查找也属于一种有序查找算法。

相对于折半查找，一般将待比较的key值与第mid=（low+high）/2位置的元素比较，比较结果分三种情况：

• 1）相等，mid位置的元素即为所求
• 2）>，low=mid+1;
• 3）<，high=mid-1。

斐波那契查找与折半查找很相似，他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1，及n=F(k)-1;

开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1),比较结果也分为三种

• 1）相等，mid位置的元素即为所求
• 2）>，low=mid+1,k-=2;
• 说明：low=mid+1说明待查找的元素在[mid+1,high]范围内，k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个，所以可以递归的应用斐波那契查找。
• 3）<，high=mid-1,k-=1。

说明：low=mid+1说明待查找的元素在[low,mid-1]范围内，k-=1 说明范围[low,mid-1]内的元素个数为F(k-1)-1个，所以可以递归 的应用斐波那契查找。

- 斐波那契是一种特殊的分割方法，和二分、插值本质上是一样的，都是分割方法；

利用了斐波那契数列特殊的性质，一个长度只要可以被黄金分割，那么分割后的片段仍然可以继续进行黄金分割，循环。

- 3. 复杂度分析

- 最坏情况下，时间复杂度为O(log2n)，且其期望复杂度也为O(log2n)。

- 4. 代码实现

### 5. 分块查找

- 1. 基本思想

- 分块查找是折半查找和顺序查找的一种改进方法，分块查找由于只要求索引表是有序的，对 块内节点没有排序要求，因此特别适合于节点动态变化的情况。 分块查找要求把一个数据分为若干块，每一块里面的元素可以是无序的，但是块与块之间的 元素需要是有序的。即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字;而 第2块中任一元素又都必须小于第3块中的任一元素，......。

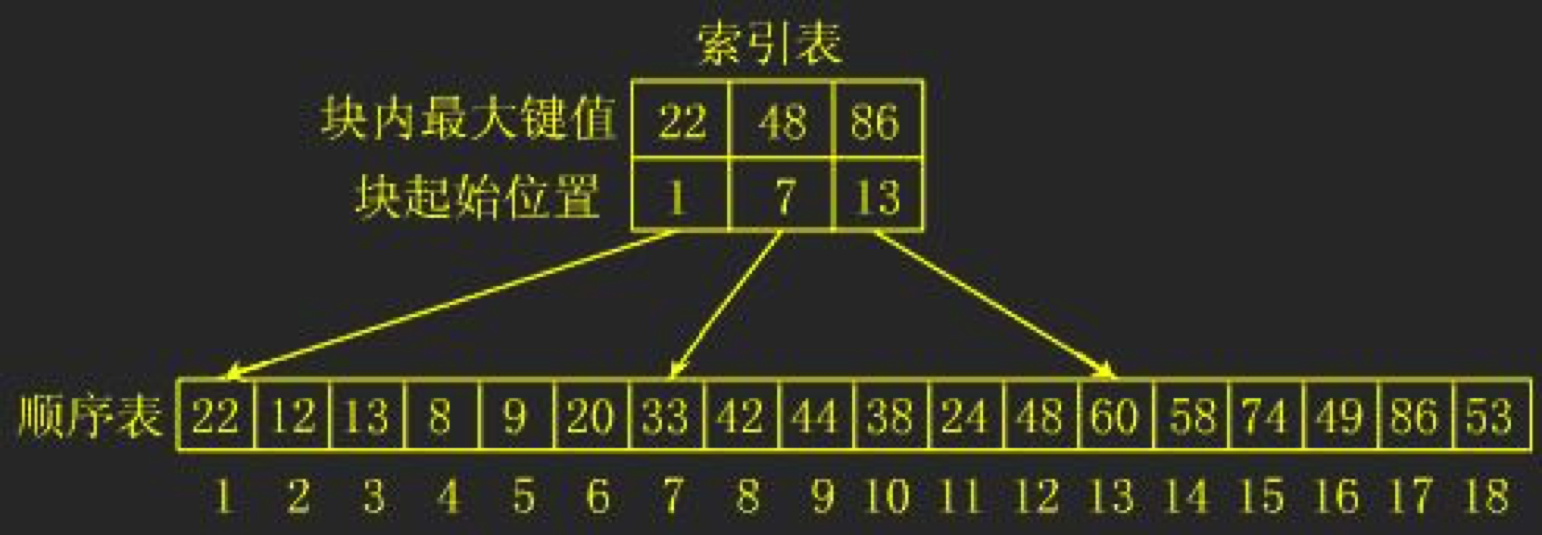
- 2. 代码实现

- 3. 复杂度分析

- 4. 应用场景分析

### 6. 哈希查找

- 1. 哈希表和哈希函数概念

- 在记录的存储位置和它的关键字之间是建立一个确定的对应关系（映射函数），使每个关键字和一个存储位置能唯一对应。

这个映射函数称为哈希函数，根据这个原则建立的表称为哈希表(Hash Table)，也叫散列表。

- 2. 哈希冲突

- 若 key1 ≠ key2 ，而 f(key1) = f(key2)，这种情况称为冲突(Collision)。

根据哈希函数f(key)和处理冲突的方法将一组关键字映射到一个有限的连续的地址集（区间）上，并以关键字在地址集中的“像”作为记录在表中的存储位置，这一映射过程称为构造哈希表。

- 3. 构造哈希表

- （1）直接定址法

- 说白了，就是小学时学过的一元一次方程。

- 即 f(key) = a * key + b。其中，a和b 是常数。

- （2）数字分析法

- 假设关键字是R进制数（如十进制）。并且哈希表中可能出现的关键字都是事先知道的，则可选取关键字的若干数位组成哈希地址。

- 选取的原则是使得到的哈希地址尽量避免冲突，即所选数位上的数字尽可能是随机的。

- （3）平方取中法

- 取关键字平方后的中间几位为哈希地址。通常在选定哈希函数时不一定能知道关键字的全部情况，仅取其中的几位为地址不一定合适；

- 而一个数平方后的中间几位数和数的每一位都相关， 由此得到的哈希地址随机性更大。取的位数由表长决定。

- （4）除留余数法

- 取关键字被某个不大于哈希表表长 m 的数 p 除后所得的余数为哈希地址。

- 即 f(key) = key % p (p ≤ m)

- 这是一种最简单、最常用的方法，它不仅可以对关键字直接取模，也可在折叠、平方取中等运算之后取模。

- 注意：p的选择很重要，如果选的不好，容易产生冲突。根据经验，一般情况下可以选p为素数。

- （5）随机数法

- 选择一个随机函数，取关键字的随机函数值为它的哈希地址，即 f(key) = random(key)。

- 通常，在关键字长度不等时采用此法构造哈希函数较为恰当。

- 4. 解析哈希冲突

- （1）开放定址法

- 如果两个数据元素的哈希值相同，则在哈希表中为后插入的数据元素另外选择一个表项。

- 当程序查找哈希表时，如果没有在第一个对应的哈希表项中找到符合查找要求的数据元素，程序就会继续往后查找，直到找到一个符合查找要求的数据元素，或者遇到一个空的表项。

- （2）拉链法

- 将哈希值相同的数据元素存放在一个链表中，在查找哈希表的过程中，当查找到这个链表时，必须采用线性查找方法。

- 在这种方法中，哈希表中每个单元存放的不再是记录本身，而是相应同义词单链表的头指针。

- 5. 实现一个哈希表

- 6. 时间复杂度

### 7. 树查找

- 1. 二叉树查找算法

- 1. 基本思想

- 二叉查找树是先对待查找的数据进行生成树，确保树的左分支的值小于右分支的值，然后在就行和每个节点的父节点比较大小，查找最适合的范围。 这个算法的查找效率很高，但是如果使用这种查找方法要首先创建树。

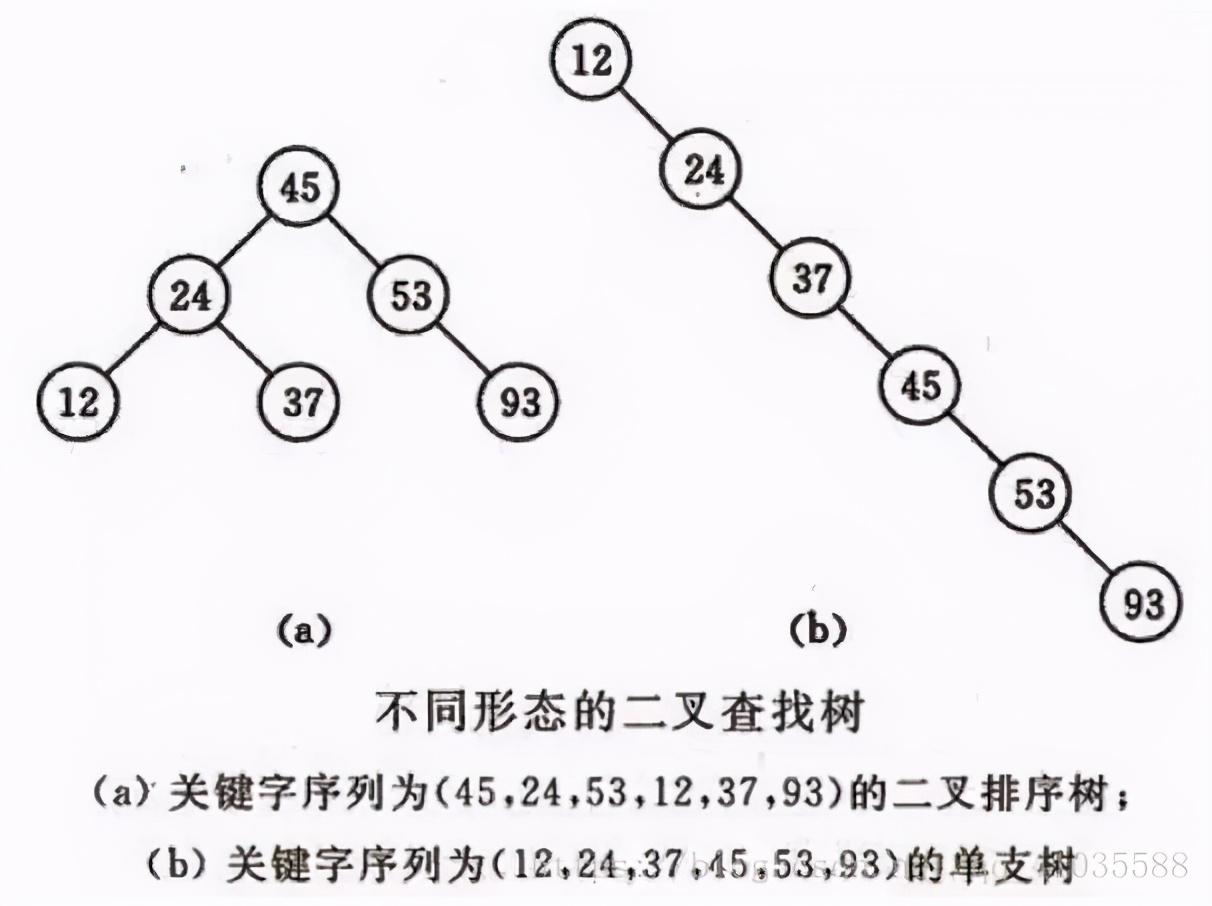
- 2. 二叉查找树性质

- 二叉查找树（BinarySearch Tree，也叫二叉搜索树，或称二叉排序树Binary Sort Tree）或者是一棵空树，或者是具有下列性质的二叉树：

• - 1）若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• - 2）若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• - 3）任意节点的左、右子树也分别为二叉查找树。
• - 4） 对二叉查找树进行中序遍历，即可得到有序的数列。

- 3. 复杂度分析

- 它和二分查找一样，插入和查找的时间复杂度均为O(logn)，但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候，树没有保持平衡（比如，我们查找上图（b）中的“93”，我们需要进行n次查找操作）。我们追求的是在最坏的情况下仍然有较好的时间复杂度，这就是平衡查找树设计的初衷。

- 4. 代码实现

- 5. 应用场景

- 2. 平衡查找树之2-3查找树（2-3 Tree）

- 1. 定义

- 2. 性质

- 3. 复杂度分析

- 4. 代码实现

- 3. 平衡查找树之红黑树（Red-Black Tree）

- 1. 定义

- 2. 基本思想

- 3. 性质

- 4. 复杂度分析

- 5. 代码实现

- 6. 应用场景

- 4. B树

- 1. 定义

- 2. 基本思想

- 3. 性质

- 4. 复杂度分析

- 5. 代码实现

- 6. 应用场景

- 5. B+树

- 1. 定义

- 2. 基本思想

- 3. 性质

- 4. 复杂度分析

- 5. 代码实现

- 6. 应用场景

- 6. 前缀树

- 1. 定义

- 2. 基本思想

- 3. 性质

- 4. 复杂度分析

- 5. 代码实现

- 6. 应用场景

- 7. 线段树

- 1. 定义

- 2. 基本思想

- 3. 性质

- 4. 复杂度分析

- 5. 代码实现

- 6. 应用场景

## 六、栈相关算法

## 七、链表相关算法

## 八、双指针相关

## 九、二叉树相关

## 十、深度优先和广度优先算法

## 十一、贪心算法

## 十二、回溯算法

## 十三、动态规划

## 参考资料

- [Java面试必备知识点梳理：二分查找算法](
https://www.toutiao.com/a6763634852416717325/)

- [顺序，二分，插值，斐波，树表，分块，哈希查找大全集及性能分析](
https://www.toutiao.com/a6772742242546221572/)

- [详解哈希表的查找](
https://www.toutiao.com/a6527689601924989453/)

- [数据结构和算法试题大全](
https://www.toutiao.com/i6903421300237353476)

- 《数据结构与算法分析Java语言描述 原书第3版 》