任何一个可以用计算机解决的问题所需的计算时间都与其规模有关系，这也就意味着，通常情况下问题规模越大，所耗费的时间和计算资源越多；而问题的规模越小，所需的时间和计算资源越小，问题的求解也越容易，因此，在处理一些困难问题的时候，我们会考虑通过缩小问题的规模而使得困难问题更加容易求解。在充分研究这类算法的规律之后，人们将这些算法总结成缩小规模算法，如递归法、分治法、动态规划法、贪心法等。（分治法、动态规划法、回溯法都是基于递归的算法）

1 穷举法

在实际解题过程中，可以发现并不是任何问题都可以直观地分解成若干小问题来进行求解，往往最容易想到的解题策略是枚举法（也称为穷举法或蛮力法），即对要解决问题的所有可能情况，一个不漏地进行检验，从中找出符合要求的答案，因此枚举法是通过牺牲时间来换取答案的全面性。如果在搜索解的过程中加上判定条件来加快搜索速度，则按搜索策略的不同有回溯法与分支限界算法。

2 回溯法

回溯法（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。扩大当前候选解的规模，并继续试探的过程称为向前试探。也就是如果当前候选解除了不满足规模要求外，满足其他所有要求时，继续扩大当前候选解的规模，并继续试探。如果当前的候选解满足包括问题规模在内的所有要求时，该候选解就是问题的一个解。

回溯算法实际上是一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯“返回，尝试别的路径。可以参考一下走迷宫的过程，一开始会随机选择一条道路前进，一直到走不通之后就会回头直到找到另外一条没有试过的道路前进。实际上，走迷宫的算法就是回溯法的经典问题。

回溯法实际上也是一种试错的思路，通过不断尝试解的组合来达到求解可行解和最优解的目的。虽然都有穷搜的概念蕴含其中，但是回溯法和穷举查找法是不同的。对于一个问题的所有实例，穷举法注定都是非常缓慢的，但应用回溯法至少可以期望对于一些规模不是很小的实例，计算机在可接受的时间内对问题求解。

回溯，正如去某一个地方要回到原点一样，需要记住回溯点的状态，栈或递归栈就是适合的一个方式。

许多复杂的规模的问题都可以使用回溯法，有”通用解题方法”的美称。分书问题和八皇后都是典型的回溯法问题。

3 递归算法及代码执行流程

在递归函数中，递归分为两个阶段，递推与回归，递推执行递归函数自调用处之前的代码，回归时执行递归函数自调用处之后的代码。

参考：
https://www.toutiao.com/i6741249809774019084/

《C++｜从函数内部的执行顺序理解递归的整体顺序》

4 分书问题

有编号为0，1，2，3，4的5本书，准备分给5个人A，B，C，D，E，写一个程序，输出所有皆大欢喜的分书方案。

每个人的阅读兴趣用一个二维数组like描述：

Like[i][j] = true i喜欢书j

Like[i][j] = false i不喜欢书j

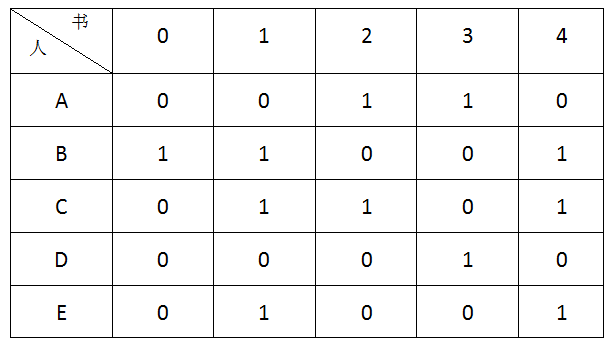
设计一个函数trynext(int i)给第i个人分书。

用一个一维数组take表示某本书分给了某人。take[j]=i+1;//把第j本书分配给第i个人

依次尝试把书j分给人i。

如果第i个人不喜欢第j本书，则尝试下一本书，如果喜欢，并且第j本书尚未分配，则把书j分配给i。

如果i是最后一个人，则方案数加1，输出该方案。否则调用trynext(i+1)为第i+1个人分书。

如果对第i个人枚举了他喜欢的所有的书，都没有找到可行的方案，那就回到前一个状态i-1，让i-1把分到的书退回去，重新找喜欢的书，再递归调用函数，寻找可行的方案。

5 先直接看分书问题的代码

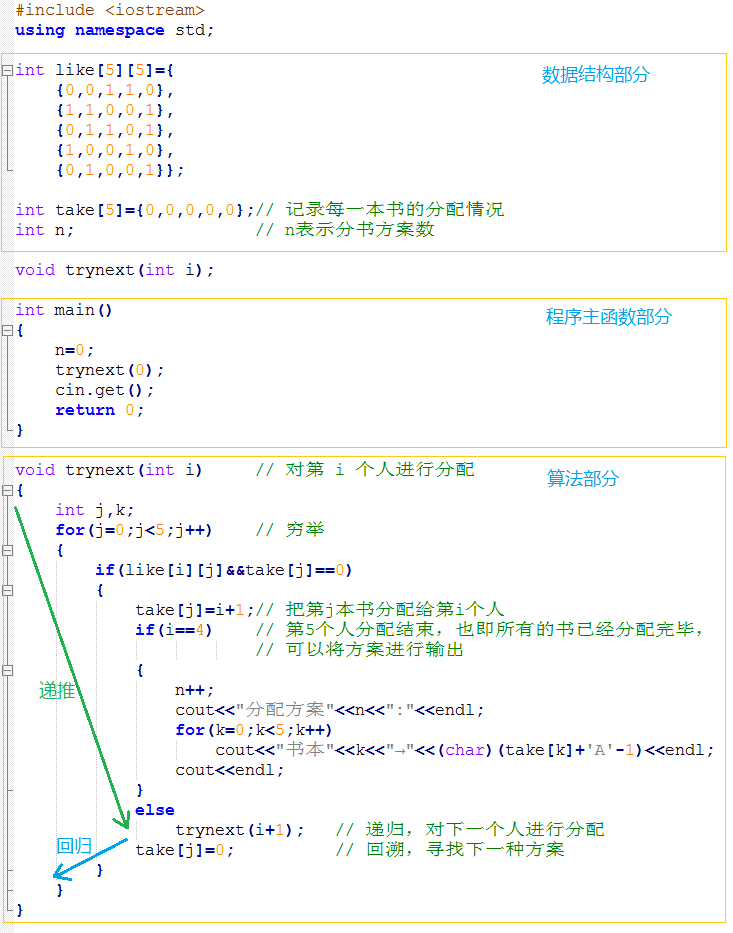
运行结果：

分配方案1:书本0→B书本1→C书本2→A书本3→D书本4→E分配方案2:书本0→B书本1→E书本2→A书本3→D书本4→C分配方案3:书本0→D书本1→B书本2→C书本3→A书本4→E分配方案4:书本0→D书本1→E书本2→C书本3→A书本4→B

如果不考虑回溯，也就是把倒数第四行代码take[j]=0;去掉，则可得到单一解决方案。

这就是递归函数后面有没有代码可执行的区别，如果后面（回归阶段）没有代码可执行，称为尾递归，如果后面（回归阶段）有代码可执行，称为非尾递归。

第1次递归前的栈状态及各全局变量和局部变量值：

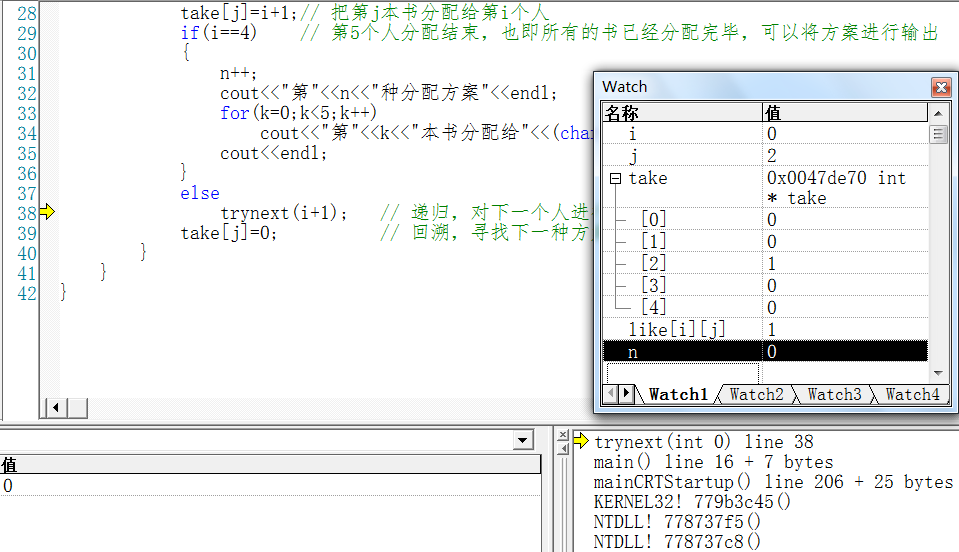
第2次递归前的栈状态及各全局变量和局部变量值：

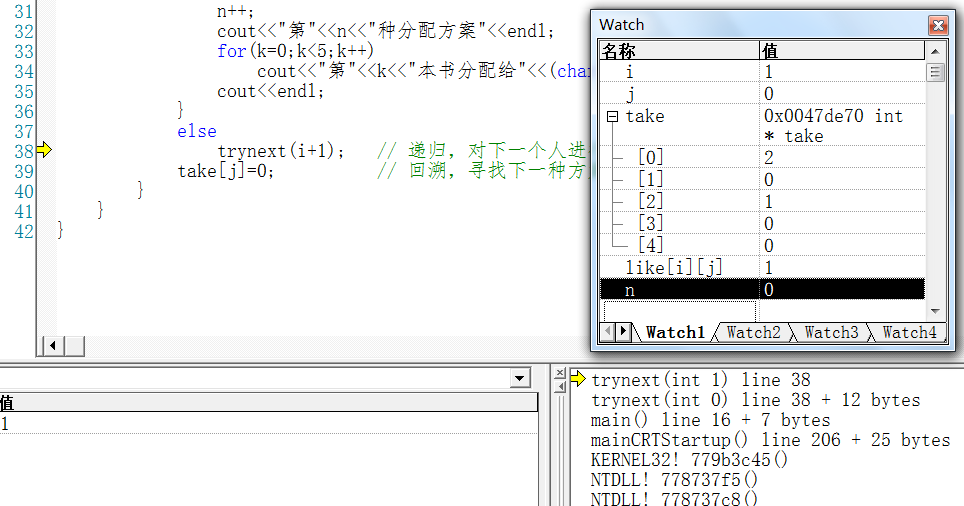
第3次递归前的栈状态及各全局变量和局部变量值：

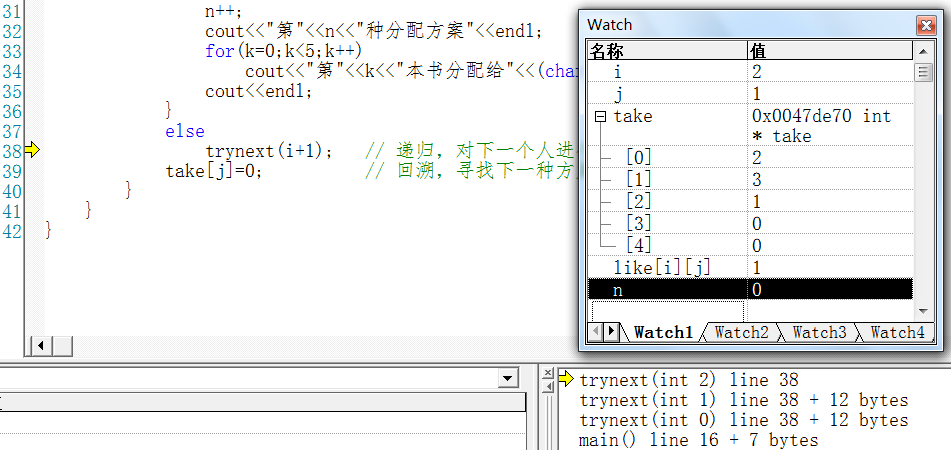
第4次递归前的栈状态及各全局变量和局部变量值：

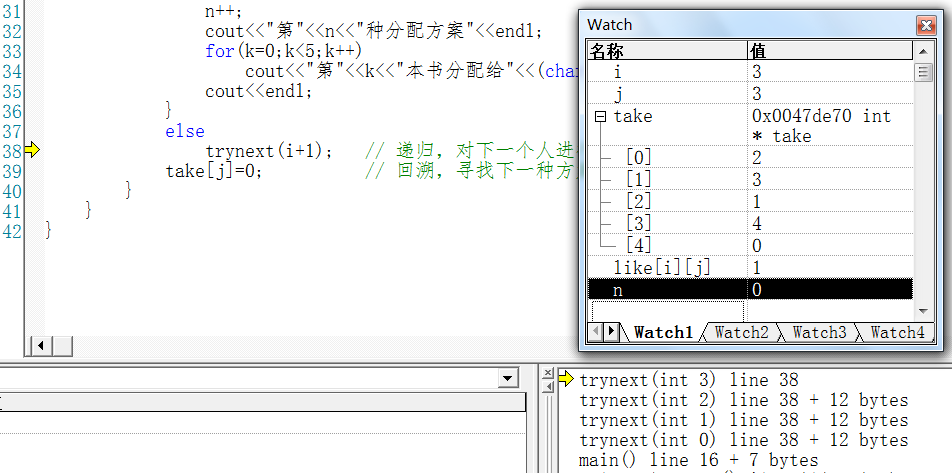
6 回溯的执行流程

6.1 第一个回溯点（递归函数回归点）：i=4; j=4;

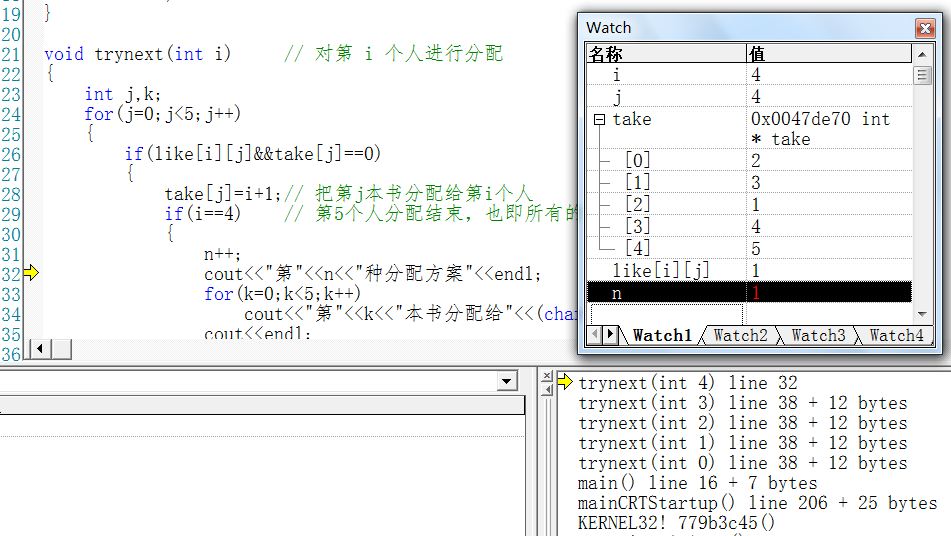
take[4] = 0;

j++;

j=5;不满足j<5的条件，回到下一个递归点。

6.2 第2个回溯点（递归函数回归点）：i=3; j=3;

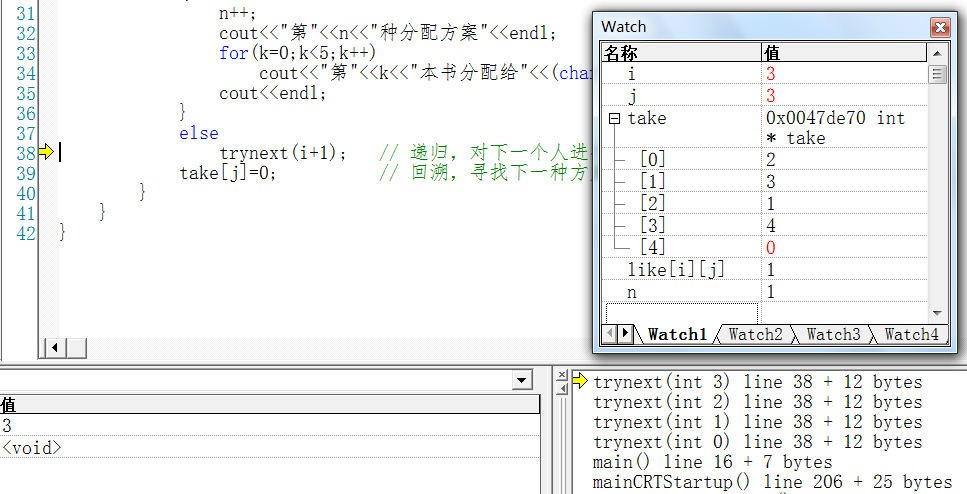
take[3] = 0;

j++;

j=4;

j++;

j=5;不满足j<5的条件，回到下一个递归点。

6.3 第3个回溯点（递归函数回归点）：i=2; j=1;

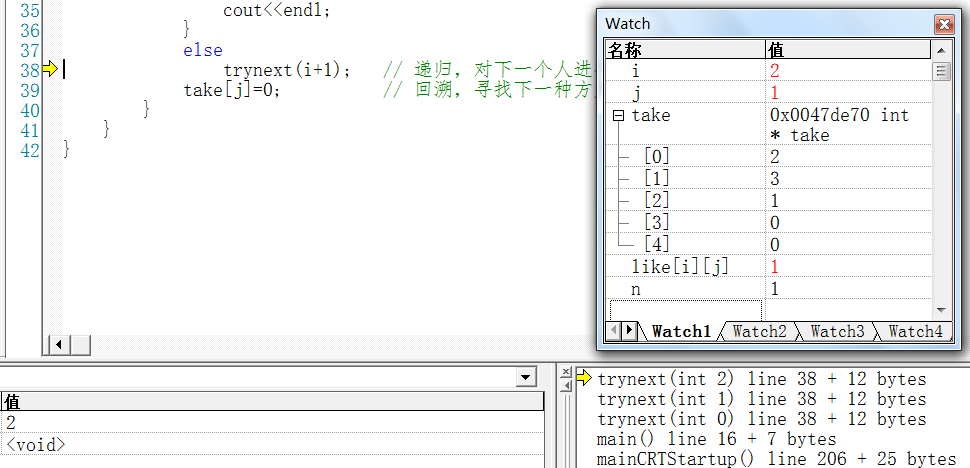
take[1] = 0;

j++;

j=2;

like[2][2]=1、take[2] = 1

j++;

j=3

like[2][3]=0

j++;

j=4;

like[2][4]=1、take[4] = 0

take[4] = 2+1 = 3

i=4 不成立；

递归：trynext(3)

开始递推：

i = 3; j=0;

j++

j++

j++

take[3] = 3+1

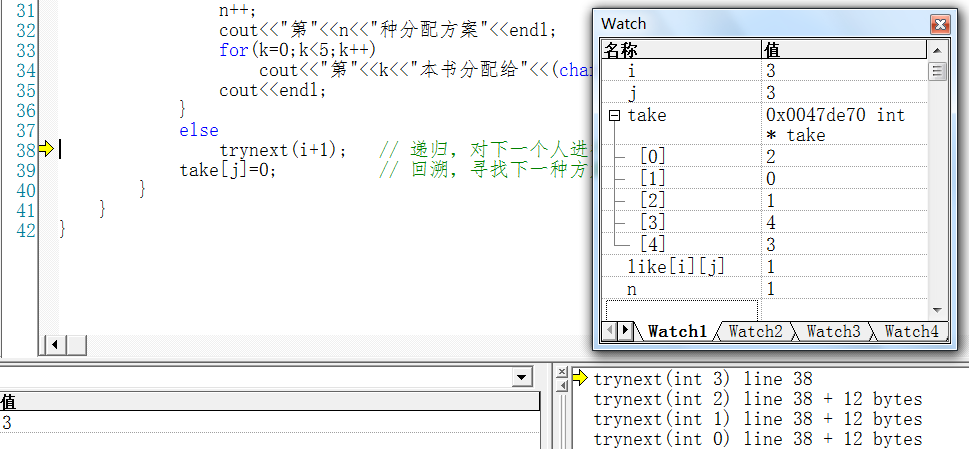
i=4 不成立；

递归：trynext(4)

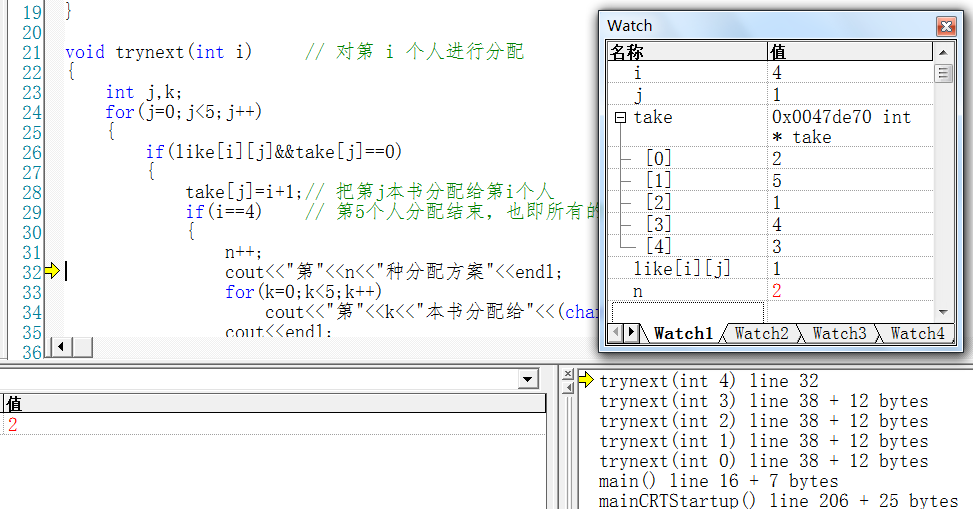
开始递推：

i = 4; j=0;

j++

take[1] = 4+1

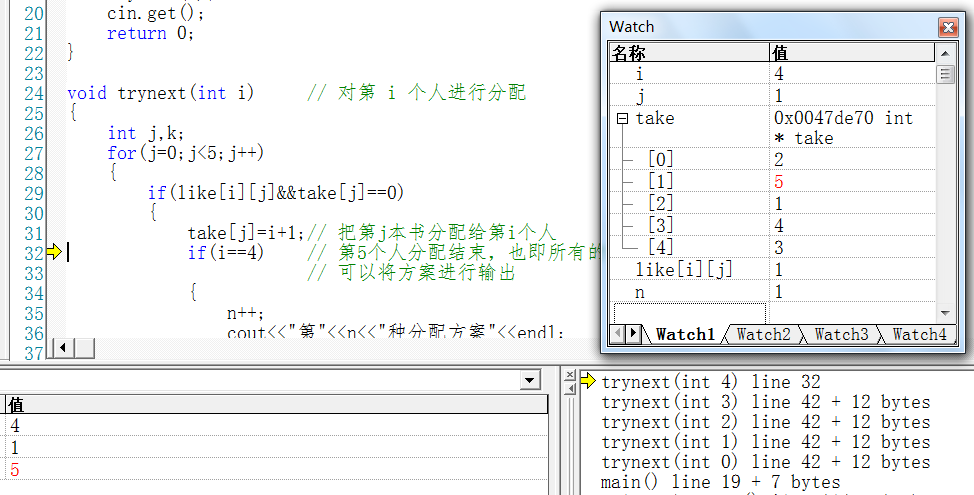
至此，又得到了一个新的方案。

然后再次在栈中进行回归（或递归、递推）……

直到得到全部解决方案。

－End－